汇编基础----整数与浮点数的机器表示
A.数制
权重,权位指的是进制的(位数-1)次冥,第n位数字的表示值等于数字乘以进制的n-1次方
注意:x86中一个字2Byte,而MIPS中一个字4Byte
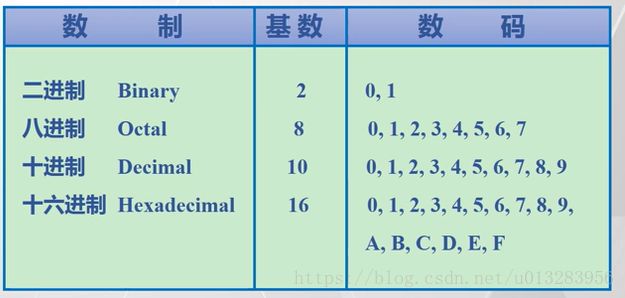
二进制:代码数1和0、逢二进一、权重是以2为底的幂。
八进制:代码数0到7、逢八进一、权重是以8为底的幂。
十进制:代码数0到9、逢十进一、权重是以10为底的幂。
十六进制:代码数0到9,A到F(代表10到16)、权重是以16为底的幂。
例:二进制(10110.011)
=1*2^4+0*2^3+1*2^2+1*2^1+0*2^0+1*2^-1+1*2^-2+1*2^-3=(22.375)十进制B.数制之间的转换
向十进制转换(按权展开)上例子中。
十进制向其他进制的转换(除以其他进制的权重取余法)
例:(十进制112.25转换成二进制数)
对整数、小数分开进行转换。
整数转换:(除转换数取余数)
112/2=56...余数0->b0(低位)
56/2=28...余数0
28/2=14...余数0
14/2=7...余数0
7/2=3...余数1
3/2=1...余数1
1/2=0...余数1
小数转换:(乘转换数取整)
0.25*2=0.5...整数=0(高位)
0.5*2=1.0...整数=1
So:(112.25)=(1110000.01)以小数点为基准,每4位一组、不够补零。
十六进制向二进制转换(与上面差不多,反方向操作。)
C.逻辑运算
D.数的机器表示(初步)
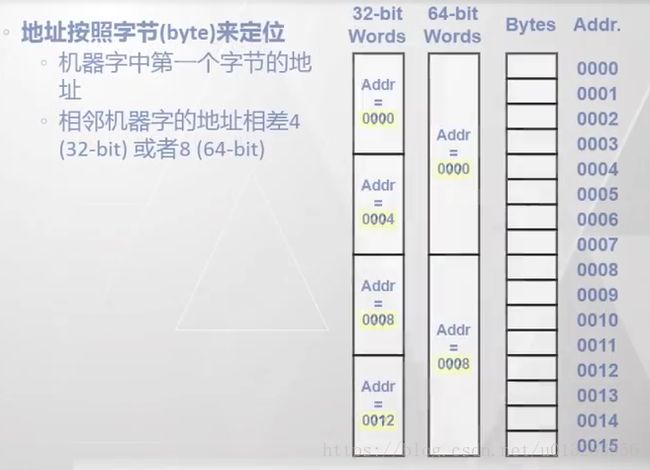
机器字长(W):指计算机进行一次整数运算所能处理的二进制数据的位数。32位宽、64位宽(也包括数据地址长度)
机器字在内存中的排序:
一个机器字如何排列: (两种排序方式。)
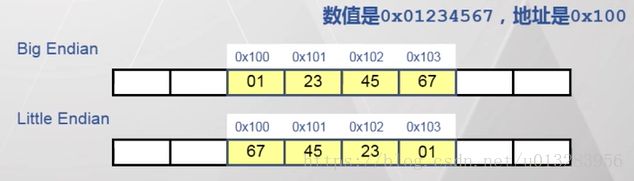
1.Big Endian(大端):Sun、PowerPC、Internet、Sparc
低位字节占据高位地址、高位字节占据低位地址。
2.Little Endian(小端):x86、IA32
与一相反。低位字节占低位地址、高位字节占据高位地址。
图解:
E.整数表示(二进制表示)
整数分类:无符号(unsigned)、有符号(signed)。(负数用补码表示整数的符号位)
机器数三种表示方式:
原码:正数0、负数1
反码:作用把减法变加法、正数的反码与原码相同、负数的反码是该数对应的正数按位取反(包括符号位)。
补码:用于带符号数、正数的补码是原码、负数的补码相应的二进制位取反加一(包括符号位)。
带符号数:其数的二进制最高位表示符号位,最高位如果是1表示带符号负数,为0表示带符号正数。
无符号与有符号的区别:取值范围,无符号大于等于0,带符号有负数也有正数包括0(用补码表示)。
取值范围(w机器字长):
| 名称 | MAX | MIN |
| 无符号 | 2^(w-1) | 0 |
| 带符号 | 2^(w-1)-1 | -2^(w-1) |
C语言常数默认是带符号数。除非末尾加U表示无符号数。
如果无符号数与带符号数混合使用,则带符号数默认转换为无符号数。(包括比较操作符)
无符号数使用建议:建议模运算,按位运算时才用无符号数。
无符号数与有符号数的加法注意溢出。乘法是一种与的操作表示。
除法:[ X / K ]
无符号数,如果除数是2的K次幂。采用逻辑右移(被除数二进制数移K位,前面位数补零。即:[ X / 2^K ] , 逻辑右移K位,前面补零。)
带符号数,被除数为正采用逻辑右移,如果是负数还需被除数先加上[ (X+2^K-1)/ 2^K]然后在逻辑右移K位。
二.浮点数的机器表示
1.IEEE的浮点数标准
数字形式:(-1)^s M 2^E
符号位s、尾数M是一个位于区间[1.0,2.0]内的小数、阶码E
编码:
| s | exp[E] | frac[M] |
双精度浮点数:exp域宽度为11 bits,frac域宽度为52bits,总共64 bits。
扩展精度浮点数:exp域宽度为15 bits,frac域宽度为63bits,总共80 bits。(1 bit 无用)
浮点数类型:
A.规格化浮点数
当尾数得值不为0时,尾数域的最高有效位应为1。(相对与1.0较近的浮点数)
在机器中表示一个浮点数时需要给出指数,这个指数用整数形式表示,这个整数叫做阶码,阶码指明了小数点在数据中的位置。
B.非规格化浮点数
非常接近于0.0的数.
C.一些特殊值
正无穷与负无穷。以及计算机无法表达的一些数。
满足条件:exp = 111..1
三种类型示意图:
最中间的是规格化浮点数,然后非规格化,最外面的是一些特殊值。
浮点数的比较:几乎可以采用无符号无符号整数的比较方式。
2.舍入(Rounding)
给定一个数,如何给出其浮点数表示?
流程:首先计算其精确值,然后将其转换为所需的精度。(可能会溢出指数的绝对值非常大,可能需要舍入)
舍入方式:(向最接近值舍入)向偶数舍入。
4种舍入方式:
| 初始值 | 舍入值 | 舍入方式 |
| 1.2349999 | 1.23 | Less than half way(小于一半,丢弃) |
| 1.2350001 | 1.24 | Greater than half way(大于一半,前面是奇数,取入) |
| 1.2350000 | 1.24 | Half way——round up(等于一半,前面是奇数,取入) |
| 1.2450000 | 1.24 | Half way——round down(等于一半,前面是偶数,丢弃) |
3.C语言中的浮点数
float 单精度浮点数
double 双精度浮点数
类型转换:
int、float、double等类型转换时
1.double或float转换为int:
尾数部分截断。
如果溢出或浮点数是NaN(特殊值),则转换结果没有定义。通常置为最大值或者最小值。
2.int转换为double:能够精确转换。
3.int转换为float:不会溢出,但是可能被舍入。
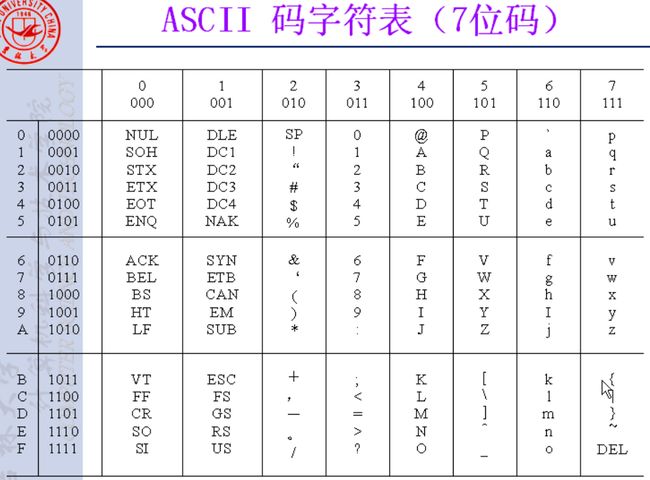
补图ASCII字符编码:(交叉看,如:A=41)