数学推导+纯Python实现机器学习算法25：kmeans聚类

Python机器学习算法实现

Author：louwill

Machine Learning Lab

     

聚类分析（Cluster Analysis）是一类经典的无监督学习算法。在给定样本的情况下，聚类分析通过特征相似性或者距离的度量方法，将其自动划分到若干个类别中。常用的聚类分析方法包括层次聚类法（Hierarchical Clustering）、k均值聚类（K-means Clustering）、模糊聚类（Fuzzy Clustering）以及密度聚类（Density Clustering）等。本节我们仅对最常用的kmeans算法进行讲解。

相似度度量

相似度或距离度量是聚类分析的核心概念。常用的距离度量方式包括闵氏距离和马氏距离，常用的相似度度量方式包括相关系数和夹角余弦等。

• 闵氏距离
  闵氏距离即闵可夫斯基距离（Minkowski Distance），定义如下。给定 维向量样本集合 ，对于 ， ，，样本 与样本 之间的闵氏距离可定义为：
  ，
  当 时，闵氏距离就可以表达为欧式距离（Euclidean Distance）：
  
  当 时，闵氏距离也称为曼哈顿距离（Manhatan Distance）：
  
  当 时，闵氏距离也称为切比雪夫距离（Chebyshev Distance）：
  

• 马氏距离
  马氏距离全称为马哈拉诺比斯距离（Mahalanobis Distance），即一种考虑各个特征之间相关性的聚类度量方式。给定一个样本集合 ，其协方差矩阵为 ，样本 与样本 之间的马氏距离可定义为：
  
  当 为单位矩阵时，即样本的各特征之间相互独立且方差为1时，马氏距离就是欧式距离。

• 相关系数
  相关系数（Correlation Coefficent）是度量相似度最常用的方式。相关系数越接近于1表示两个样本越相似，相关系数越接近于0，表示两个样本越不相似。样本 和 之间相关系数可定义为：
  

• 夹角余弦
  夹角余弦也是度量两个样本相似度的方式之一。夹角余弦越接近于1表示两个样本越相似，夹角余弦越接近于0，表示两个样本越不相似。样本 和 之间夹角余弦可定义为：
  

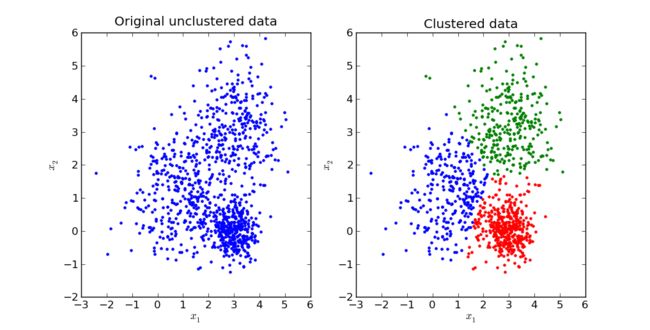
kmeans聚类

kmeans即k均值聚类算法。给定 维样本集合 ， 均值聚类是要将 个样本划分到 个不同的类别区域，通常而言 。所以 均值聚类可以总结为对样本集合 的划分，其学习策略主要是通过损失函数最小化来选取最优的划分。

我们使用欧式距离作为样本间距离的度量方式。则样本间的距离 可定义为：

定义样本与其所属类中心之间的距离总和为最终损失函数：

其中为第 个类的质心（即中心点）， 中 表示指示函数，取值为1或0。函数 表示相同类中样本的相似程度。所以 均值聚类可以规约为一个优化问题求解：

该问题是一个NP hard的组合优化问题，实际求解时我们采用迭代的方法进行求解。

根据以上定义，我们可以梳理 均值聚类算法的主要流程如下：

• 初始化质心。即在第0次迭代时随机选择 个样本点作为初始化的聚类质心点。

• 按照样本与中心的距离对样本进行聚类。对固定的类中心，其中 为类 的中心点，计算每个样本到类中心的距离，将每个样本指派到与其最近的中心点所在的类，构成初步的聚类结果 。

• 计算上一步聚类结果的新的类中心。对聚类结果 计算当前各个类中样本均值，并作为新的类中心。

• 如果迭代收敛或者满足迭代停止条件，则输出最后聚类结果 ，否则令 ，返回第二步重新计算。

kmeans算法实现

下面我们基于numpy按照前述算法流程来实现一个kmeans算法。回顾上述过程，我们可以先思考一下对算法每个流程该如何定义。首先要定义欧式距离计算函数，然后类中心初始化、根据样本与类中心的欧式距离划分类别并获取聚类结果、根据新的聚类结果重新计算类中心点、重新聚类直到满足停止条件。

下面我们先定义两个向量之间的欧式距离函数如下：

import numpy as np
# 定义欧式距离
def euclidean_distance(x1, x2):
    distance = 0
    # 距离的平方项再开根号
    for i in range(len(x1)):
        distance += pow((x1[i] - x2[i]), 2)
    return np.sqrt(distance)

然后为每个类别随机选择样本进行类中心初始化：

# 定义中心初始化函数
def centroids_init(k, X):
    n_samples, n_features = X.shape
    centroids = np.zeros((k, n_features))
    for i in range(k):
        # 每一次循环随机选择一个类别中心
        centroid = X[np.random.choice(range(n_samples))]
        centroids[i] = centroid
    return centroids

根据欧式距离计算每个样本所属最近类中心点的索引：

# 定义样本的最近质心点所属的类别索引
def closest_centroid(sample, centroids):
    closest_i = 0
    closest_dist = float('inf')
    for i, centroid in enumerate(centroids):
        # 根据欧式距离判断，选择最小距离的中心点所属类别
        distance = euclidean_distance(sample, centroid)
        if distance < closest_dist:
            closest_i = i
            closest_dist = distance
    return closest_i

定义构建每个样本所属类别过程如下：

# 定义构建类别过程
def create_clusters(centroids, k, X):
    n_samples = np.shape(X)[0]
    clusters = [[] for _ in range(k)]
    for sample_i, sample in enumerate(X):
        # 将样本划分到最近的类别区域
        centroid_i = closest_centroid(sample, centroids)
        clusters[centroid_i].append(sample_i)
    return clusters

根据上一步聚类结果重新计算每个类别的均值中心点：

# 根据上一步聚类结果计算新的中心点
def calculate_centroids(clusters, k, X):
    n_features = np.shape(X)[1]
    centroids = np.zeros((k, n_features))
    # 以当前每个类样本的均值为新的中心点
    for i, cluster in enumerate(clusters):
        centroid = np.mean(X[cluster], axis=0)
        centroids[i] = centroid
    return centroids

然后简单定义一下如何获取每个样本所属的类别标签：

# 获取每个样本所属的聚类类别
def get_cluster_labels(clusters, X):
    y_pred = np.zeros(np.shape(X)[0])
    for cluster_i, cluster in enumerate(clusters):
        for sample_i in cluster:
            y_pred[sample_i] = cluster_i
    return y_pred

最后我们将上述过程进行封装，定义一个完整的kmeans算法流程：

# 根据上述各流程定义kmeans算法流程
def kmeans(X, k, max_iterations):
    # 1.初始化中心点
    centroids = centroids_init(k, X)
    # 遍历迭代求解
    for _ in range(max_iterations):
        # 2.根据当前中心点进行聚类
        clusters = create_clusters(centroids, k, X)
        # 保存当前中心点
        prev_centroids = centroids
        # 3.根据聚类结果计算新的中心点
        centroids = calculate_centroids(clusters, k, X)
        # 4.设定收敛条件为中心点是否发生变化
        diff = centroids - prev_centroids
        if not diff.any():
            break
    # 返回最终的聚类标签
    return get_cluster_labels(clusters, X)

我们来简单测试一下上述实现的kmeans算法：

# 测试数据
X = np.array([[0,2],[0,0],[1,0],[5,0],[5,2]])
# 设定聚类类别为2个，最大迭代次数为10次
labels = kmeans(X, 2, 10)
# 打印每个样本所属的类别标签
print(labels)

[0. 0. 0. 1. 1.]

可以看到，kmeans算法将第1~3个样本聚为一类，第4~5个样本聚为一类。sklearn中也为我们提供了kmeans算法的接口，尝试用sklearn的kmeans接口来测试一下该数据：

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
print(kmeans.labels_)

[0. 0. 0. 1. 1.]

可以看到sklearn的聚类结果和我们自定义的kmeans算法是一样的。但是这里有必要说明的一点是，不同的初始化中心点的选择对最终结果有较大影响，自定义的kmeans算法和sklearn算法计算出来的结果一致本身也有一定的偶然性。另外聚类类别k的选择也需要通过一定程度上的实验才能确定。

参考资料：

李航 统计学习方法 第二版

往期精彩：

数学推导+纯Python实现机器学习算法27：LDA线性判别分析

数学推导+纯Python实现机器学习算法28：奇异值分解SVD

---

一个算法工程师的成长之路

长按二维码.关注机器学习实验室

喜欢您就点个在看！