力扣第191场周赛小结

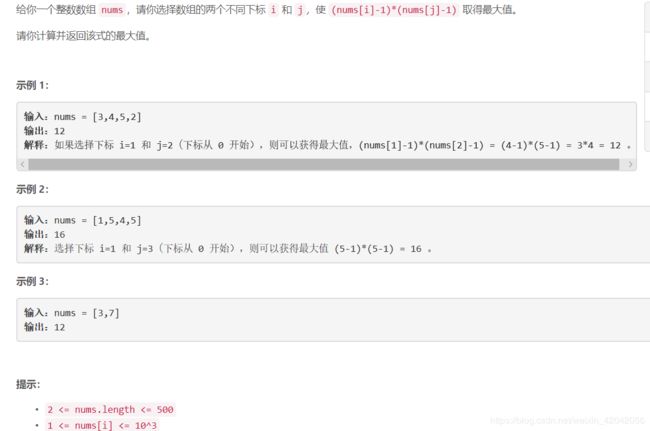
一、数组中两元素的最大乘积

1、题目描述：

2、题解：

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        n = len(nums)
        if n < 2:
            return 0
        if n == 2:
            return (nums[0] - 1) * (nums[1] - 1)
        res = 0
        for i in range(n-1):
            temp = nums[i] - 1
            for j in range(i+1,n):
                res = max(res,temp * (nums[j] - 1))
        return res

二、切割后面积最大的蛋糕

1、题目描述：

2、题解

class Solution:
    def maxArea(self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]) -> int:
        horizontalCuts.sort()
        verticalCuts.sort()
        horizontalCuts = [0] + horizontalCuts + [h]
        verticalCuts = [0] + verticalCuts + [w]
        heightmax, vertmax = horizontalCuts[0], verticalCuts[0]
        for i in range(1,len(horizontalCuts)):
            heightmax = max(heightmax,horizontalCuts[i] - horizontalCuts[i-1])
        for j in range(1,len(verticalCuts)):
            vertmax = max(vertmax,verticalCuts[j] - verticalCuts[j - 1])
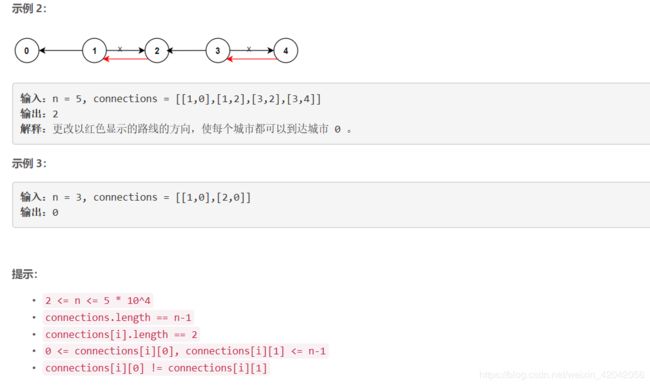
        return heightmax * vertmax % int(1e9 + 7)

三、重新规划路线

1、题目描述

2、题解

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        edges = [[] for _ in range(n)]
        for c in connections:
            edges[c[0]].append((c[1], 1))
            edges[c[1]].append((c[0], 0))
        cost = 0
        stack = [0]
        visited = [False] * n
        visited[0] = True
        while len(stack) > 0:
            u = stack.pop(-1)
            for v, c in edges[u]:
                if not visited[v]:
                    visited[v] = 1
                    cost += c
                    stack.append(v)
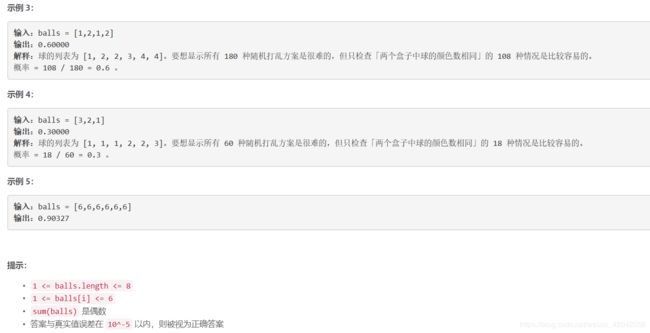
        return cost

四、两个盒子中球的颜色数相同的概率

1、题目描述

2、题解

class Solution:
    def C(self, m, n):
        return self.fac[n] / self.fac[m] / self.fac[n - m]

    def DFS(self, p, cl, cr, nl, nr):
        if p == len(self.balls):
            if cl == cr:
                return 1.
            return 0.
        if abs(cl - cr) > len(self.balls) - p:
            return 0.
        ans = 0.
        for i in range(1, self.balls[p]):
            j = self.balls[p] - i
            if nl - i < 0 or nr - j < 0:
                continue
            ans += self.DFS(p + 1, cl + 1, cr + 1, nl - i, nr - j) * \
                   self.C(i, nl) * self.C(j, nr) / self.C(i + j, nl + nr)
        q = self.balls[p]
        if nl >= q:
            ans += self.DFS(p + 1, cl + 1, cr, nl - q, nr) * \
                   self.C(q, nl) / self.C(q, nl + nr)
        if nr >= q:
            ans += self.DFS(p + 1, cl, cr + 1, nl, nr - q) * \
                   self.C(q, nr) / self.C(q, nl + nr)
        return ans

    def getProbability(self, balls):
        self.fac = [1., 1.]
        for i in range(2, 49):
            self.fac.append(self.fac[-1] * i)
        self.balls = balls
        n = int(sum(balls) / 2)
        return self.DFS(0, 0, 0, n, n)