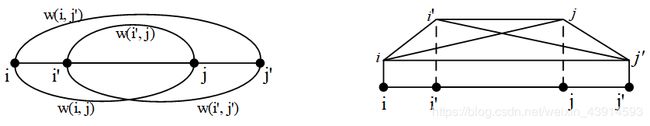算法竞赛专题解析(10):DP优化(1)--四边形不等式
本系列文章将于2021年整理出版,书名《算法竞赛专题解析》。
前驱教材:《算法竞赛入门到进阶》 清华大学出版社 2019.8
网购:京东 当当 作者签名书
如有建议,请加QQ 群:567554289,或联系作者QQ:15512356
文章目录
- 1 理论背景
- 2 应用场合
- 3 四边形不等式优化
- 4 四边形不等式定义和单调性定义
- 5 四边形不等式定理(Knuth-Yao DP Speedup Theorem)
- 6 证明四边形不等式定理
- 7 一维决策单调性优化
- 8 例题
《算法竞赛入门到进阶》的第7章“动态规划”,讲解了DP的概念,以及线性DP、区间DP、树形DP、数位DP、状态压缩DP等应用场景。
本文以及后续几篇,将介绍DP的优化技术。
四边形不等式DP优化涉及的证明比较复杂,如果先给出定义和证明会让人迷惑,所以本文的组织结构是:先给出应用场景,引导出四边形不等式的概念,再进行定义和证明,最后用例题巩固。
四边形不等式DP优化,虽然理论有点复杂,但是编码很简单。
1 理论背景
四边形不等式(quadrangle inequality)应用于DP优化,是一个古老的知识点。它起源于Knuth(高纳德)1971年的一篇论文1,用来解决最优二叉搜索树问题。1980年,储枫(F. Frances Yao,姚期智的夫人)做了深入研究2,扩展为一般性的DP优化方法,把一些复杂度 O ( n 3 ) O(n^3) O(n3)的DP问题,优化为 O ( n 2 ) O(n^2) O(n2)。所以这个方法又被称为“Knuth-Yao DP Speedup Theorem”。
2 应用场合
有一些常见的DP问题,通常是区间DP问题,它的状态转移方程是:
d p [ i ] [ j ] = m i n ( d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + w [ i ] [ j ] ) dp[i][j] = min(dp[i][k] + dp[k + 1][j] + w[i][j]) dp[i][j]=min(dp[i][k]+dp[k+1][j]+w[i][j])
其中 i < = k < j i <= k < j i<=k<j,初始值 d p [ i ] [ i ] dp[i][i] dp[i][i]已知。 m i n ( ) min() min()也可以是 m a x ( ) max() max(),见本文第6小节的说明。
方程的含义是:
(1) d p [ i ] [ j ] dp[i][j] dp[i][j]表示从 i i i状态到 j j j状态的最小花费。题目一般是求 d p [ 1 ] [ n ] dp[1][n] dp[1][n],即从起始点 1 1 1到终点 n n n的最小花费。
(2) d p [ i ] [ k ] + d p [ k + 1 ] [ j ] dp[i][k] + dp[k + 1][j] dp[i][k]+dp[k+1][j]体现了递推关系。 k k k在 i i i和 j j j之间滑动, k k k有一个最优值,使得 d p [ i ] [ j ] dp[i][j] dp[i][j]最小。
(3) w [ i ] [ j ] w[i][j] w[i][j]的性质非常重要。 w [ i ] [ j ] w[i][j] w[i][j]是和题目有关的费用,如果它满足四边形不等式和单调性,那么用DP计算dp的时候,就能进行四边形不等式优化。
这类问题的经典的例子是“石子合并”3,它的转移矩阵就是上面的 d p [ i ] [ j ] dp[i][j] dp[i][j], w [ i ] [ j ] w[i][j] w[i][j]是从第 i i i堆石子到第 j j j堆石子的总数量。
石子合并
题目描述:有n堆石子排成一排,每堆石子有一定的数量。将n堆石子并成为一堆。每次只能合并相邻的两堆石子,合并的花费为这两堆石子的总数。经过n-1次合并后成为一堆,求总的最小花费。
输入:测试数据第一行是整数n,表示有n堆石子。接下来的一行有n个数,分别表示这n堆石子的数目。
输出:总的最小花费。
输入样例:
3
2 4 5
输出样例:
17
提示:样例的计算过程是:第一次合并2+4=6;第二次合并6+5=11;总花费6+11=17。
在阅读后面的讲解时,读者可以对照“石子合并”这个例子来理解。注意,石子合并有多种情况和解法,详情见本文的例题“洛谷P1880石子合并”。
d p [ i ] [ j ] dp[i][j] dp[i][j]是一个转移矩阵,如何编码填写这个矩阵?复杂度是多少?如果直接写 i 、 j 、 k i、j、k i、j、k的3层循环,复杂度 O ( n 3 ) O(n^3) O(n3)。
注意3层循环的写法。 d p [ i ] [ j ] dp[i][j] dp[i][j]是大区间,它从小区间 d p [ i ] [ k ] dp[i][k] dp[i][k]和 d p [ k + 1 ] [ j ] dp[k+1][j] dp[k+1][j]转移而来,所以应该先计算小区间,再逐步扩展到大区间。
for(int i=1; i<=n; i++)
dp[i][i] = 0; //初始值
for(int len = 2; len <= n; len++) //len:从小区间扩展到大区间
for(int i = 1; i <= n-len+1; i++){ // 区间起点i
int j = i + len - 1; // 区间终点j
for(int k = i; k < j; k++) //大区间[i,j]从小区间[i,k]和[k+1,j]转移而来
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
3 四边形不等式优化
只需一个简单的优化操作,就能把上面代码的复杂度变为 O ( n 2 ) O(n^2) O(n2)。这个操作就是把循环 i ≤ k < j i ≤ k < j i≤k<j改为:
s [ i ] [ j − 1 ] ≤ k ≤ s [ i + 1 ] [ j ] s[i][j-1] ≤ k ≤ s[i+1][j] s[i][j−1]≤k≤s[i+1][j]
其中 s [ i ] [ j ] s[i][j] s[i][j]记录从i到j的最优分割点。在计算 d p [ i ] [ j ] dp[i][j] dp[i][j]的最小值时得到区间 [ i , j ] [i, j] [i,j]的分割点 k k k,记录在 s [ i ] [ j ] s[i][j] s[i][j]中,用于下一次循环。
这个优化被称为四边形不等式优化。下面给出优化后的代码,优化见注释的几行代码。
for(i = 1;i <= n;i++){
dp[i][i] = 0;
s[i][i] = i; //s[][]的初始值
}
for(int len = 2; len <= n; len++)
for(int i = 1; i <= n-len+1; i++){
int j = i + len - 1;
for(k = s[i][j - 1]; k <= s[i + 1][j]; k++){ //缩小循环范围
if(dp[i][j] > dp[i][k] + dp[k + 1][j] + w[i][j]){ //是否更优
dp[i][j] = dp[i][k] + dp[k + 1][j] + w[i][j];
s[i][j] = k; //更新最佳分割点
}
}
}
代码的复杂度是多少?
代码中 i i i和 k k k这2个循环,优化前是 O ( n 2 ) O(n^2) O(n2)的。优化后,每个 i i i内部的 k k k的循环次数是 s [ i + 1 ] [ j ] − s [ i ] [ j − 1 ] s[i + 1][j] - s[i][j - 1] s[i+1][j]−s[i][j−1],其中 j = i + l e n − 1 j = i + len - 1 j=i+len−1。那么:
i = 1 i = 1 i=1时, k k k循环 s [ 2 ] [ l e n ] − s [ 1 ] [ l e n − 1 ] s[2][len] - s[1][len-1] s[2][len]−s[1][len−1]次。
i = 2 i = 2 i=2时, k k k循环 s [ 3 ] [ l e n + 1 ] − s [ 2 ] [ l e n ] s[3][len+1] - s[2][len] s[3][len+1]−s[2][len]次。
…
i = n − l e n + 1 i = n-len+1 i=n−len+1时, k k k循环 s [ n − l e n + 2 ] [ n ] − s [ n − l e n + 1 ] [ n + 1 ] s[n-len+2][n] - s[n-len+1][n+1] s[n−len+2][n]−s[n−len+1][n+1]次。
上述次数相加,总次数:
s [ 2 ] [ l e n ] − s [ 1 , l e n − 1 ] + s [ 3 ] [ l e n + 1 ] − s [ 2 , l e n ] + … + s [ n + 1 , n ] − s [ n ] [ n ] s[2][len] - s[1, len-1] + s[3][len+1] - s[2, len] + … + s[n+1,n] - s[n][n] s[2][len]−s[1,len−1]+s[3][len+1]−s[2,len]+…+s[n+1,n]−s[n][n]
= s [ n − l e n + 2 ] [ n ] − s [ 1 ] [ l e n − 1 ] = s[n-len+2][n] - s[1][len-1] =s[n−len+2][n]−s[1][len−1]
< n < n <n
i i i和 k k k循环的时间复杂度优化到了 O ( n ) O(n) O(n)。总复杂度从 O ( n 3 ) O(n^3) O(n3)优化到了 O ( n 2 ) O(n^2) O(n2)。
在后面的四边形不等式定理证明中,将更严谨地证明复杂度。
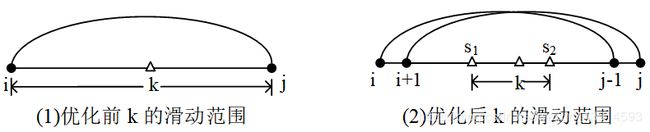
下图给出了四边形不等式优化的效果, s 1 s_1 s1是区间 [ i , j − 1 ] [i, j-1] [i,j−1]的最优分割点, s 2 s_2 s2是区间 [ i + 1 , j ] [i+1, j] [i+1,j]的最优分割点。
读者对代码可能有2个疑问:
(1)为什么能够把 i < = k < j i <= k < j i<=k<j缩小到 s [ i ] [ j − 1 ] ≤ k ≤ s [ i + 1 ] [ j ] s[i][j-1] ≤ k ≤ s[i+1][j] s[i][j−1]≤k≤s[i+1][j]?
(2) s [ i ] [ j − 1 ] ≤ s [ i + 1 ] [ j ] s[i][j-1] ≤ s[i+1][j] s[i][j−1]≤s[i+1][j]成立吗?
下面几节给出四边形不等式优化的正确性和复杂度的严谨证明,解答了这2个问题。
4 四边形不等式定义和单调性定义
在四边形不等式DP优化中,对于 w w w,有2个关键内容:四边形不等式定义、单调性。
(1)四边形不等式定义1:设 w w w是定义在整数集合上的二元函数,对于任意整数 i ≤ i ′ ≤ j ≤ j ′ i ≤ i' ≤ j ≤ j' i≤i′≤j≤j′,如果有 w ( i , j ) + w ( i ′ , j ′ ) ≤ w ( i , j ′ ) + w ( i ′ , j ) w(i, j) + w(i', j') ≤ w(i, j') + w(i', j) w(i,j)+w(i′,j′)≤w(i,j′)+w(i′,j),则称 w w w满足四边形不等式。
四边形不等式可以概况为:两个交错区间的 w w w和,小于等于小区间与大区间的 w w w和。
为什么被称为“四边形”?把它变成一个几何图,画成平行四边形,见下面图中的四边形 i ′ i j j ′ i'ijj' i′ijj′。图中对角线长度和 i j + i ′ j ′ ij+i'j' ij+i′j′大于平行线长度和 i j ′ + i ′ j ij'+i'j ij′+i′j,这与四边形的性质是相反的,所以可以理解成“反四边形不等式”。请读者注意,这个“四边形”只是一个帮助理解的示意图,并没有严谨的意义。也有其他的四边形画法,下面这种四边形是储枫论文中的画法。当中间两个点 i ′ = j i' = j i′=j时,四边形变成了一个三角形。
定义1的特例是定义2。
(2)四边形不等式定义2:对于整数 i < i + 1 ≤ j < j + 1 i < i+1 ≤ j < j+1 i<i+1≤j<j+1,如果有 w ( i , j ) + w ( i + 1 , j + 1 ) ≤ w ( i , j + 1 ) + w ( i + 1 , j ) w(i, j) + w(i+1, j+1)≤ w(i, j+1) + w(i+1, j) w(i,j)+w(i+1,j+1)≤w(i,j+1)+w(i+1,j),称 w w w满足四边形不等式。
定义1和定义2实际上是等价的,它们可以互相推导4。
(3)单调性:设w是定义在整数集合上的二元函数,如果对任意整数 i ≤ i ′ ≤ j ≤ j ′ i ≤ i' ≤ j ≤ j' i≤i′≤j≤j′,有 w ( i , j ′ ) ≥ w ( i ′ , j ) w(i, j') ≥ w(i', j) w(i,j′)≥w(i′,j),称w具有单调性。
单调性可以形象地理解为,如果大区间包含小区间,那么大区间的 w w w值超过小区间的 w w w值。
在石子合并问题中,令w[i][j]等于从第i堆石子加到第j堆石子的石子总数。它满足四边形不等式的定义、单调性:
w [ i ] [ j ′ ] ≥ w [ i ′ ] [ j ] w[i][j'] ≥ w[i'][ j] w[i][j′]≥w[i′][j],满足单调性;
w [ i ] [ j ] + w [ i ′ ] [ j ′ ] = w [ i ] [ j ′ ] + w [ i ′ ] [ j ] w[i][j] + w[i'][j'] = w[i][j'] + w[i'][j] w[i][j]+w[i′][j′]=w[i][j′]+w[i′][j],满足四边形不等式定义。
利用 w w w的四边形不等式、单调性的性质,可以推导出四边形不等式定理,用于DP优化。
5 四边形不等式定理(Knuth-Yao DP Speedup Theorem)
在储枫的论文中,提出并证明了四边形不等式定理。
四边形不等式定理:如果 w ( i , j ) w(i, j) w(i,j)满足四边形不等式和单调性,则用DP计算 d p [ ] [ ] dp[][] dp[][]的时间复杂度是 O ( n 2 ) O(n^2) O(n2)的。
这个定理是通过下面2个更详细的引理来证明的。
引理1:状态转移方程 d p [ i ] [ j ] = m i n ( d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + w [ i ] [ j ] ) dp[i][j] = min(dp[i][k] + dp[k + 1][j] + w[i][j]) dp[i][j]=min(dp[i][k]+dp[k+1][j]+w[i][j]),如果 w [ i ] [ j ] w[i][j] w[i][j]满足四边形不等式和单调性,那么 d p [ i ] [ j ] dp[i][j] dp[i][j]也满足四边形不等式。
引理2:记 s [ i ] [ j ] = k s[i][j] = k s[i][j]=k是 d p [ i ] [ j ] dp[i][j] dp[i][j]取得最优值时的 k k k,如果 d p dp dp满足四边形不等式,那么有 s [ i ] [ j − 1 ] ≤ s [ i ] [ j ] ≤ s [ i + 1 ] [ j ] s[i][j-1] ≤ s[i][j] ≤ s[i+1][j] s[i][j−1]≤s[i][j]≤s[i+1][j],即 s [ i ] [ j − 1 ] ≤ k ≤ s [ i + 1 ] [ j ] s[i][j-1] ≤ k ≤ s[i+1][j] s[i][j−1]≤k≤s[i+1][j]。
定理2直接用于DP优化,复杂度 O ( n 2 ) O(n^2) O(n2)。
6 证明四边形不等式定理
这里翻译储枫论文中对引理1和引理2的证明,并加上了本作者的一些说明。
定义方程 c ( i , j ) c(i, j) c(i,j):
c ( i , i ) = 0 c(i, i) = 0 c(i,i)=0
c ( i , j ) = w ( i , j ) + m i n ( c ( i , k − 1 ) + c ( k , j ) ) c(i, j) = w(i, j) + min(c(i, k-1) + c(k, j)) c(i,j)=w(i,j)+min(c(i,k−1)+c(k,j)) i < k ≤ j i < k ≤ j i<k≤j ( 6 − 1 ) (6-1) (6−1)
前面的例子 d p [ i ] [ j ] dp[i][j] dp[i][j]和这里的 c ( i , j ) c(i, j) c(i,j)略有不同, d p [ i ] [ j ] = m i n ( d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + w [ i ] [ j ] ) dp[i][j] = min(dp[i][k] + dp[k + 1][j] + w[i][j]) dp[i][j]=min(dp[i][k]+dp[k+1][j]+w[i][j]),其中 w [ i ] [ j ] w[i][j] w[i][j]在 m i n ( ) min() min()内部。证明过程是一样的。
公式(6-1)的 w w w要求满足四边形不等式:
w ( i , j ) + w ( i ′ , j ′ ) ≤ w ( i ′ , j ) + w ( i , j ′ ) w(i, j) + w(i', j') ≤ w(i', j) + w(i, j') w(i,j)+w(i′,j′)≤w(i′,j)+w(i,j′) i ≤ i ′ ≤ j ≤ j ′ i ≤ i' ≤ j ≤ j' i≤i′≤j≤j′ ( 6 − 2 ) (6-2) (6−2)
而且要求 w w w是单调的: w ( i ′ , j ) ≤ w ( i , j ′ ) w(i', j) ≤ w(i, j') w(i′,j)≤w(i,j′) [ i ′ , j ] ⊆ [ i , j ′ ] [i', j]\subseteq[i, j'] [i′,j]⊆[i,j′]
(1)证明引理1
引理1:如果 w ( i , j ) w(i, j) w(i,j)满足四边形不等式和单调性,那么 c ( i , j ) c(i, j) c(i,j)也满足四边形不等式:
c ( i , j ) + c ( i ′ , j ′ ) ≤ c ( i ′ , j ) + c ( i , j ′ ) c(i, j) + c(i', j') ≤ c(i', j) + c(i, j') c(i,j)+c(i′,j′)≤c(i′,j)+c(i,j′) i ≤ i ′ ≤ j ≤ j ′ i≤i'≤j≤j' i≤i′≤j≤j′ ( 6 − 3 ) (6-3) (6−3)
下面证明(6-3)。
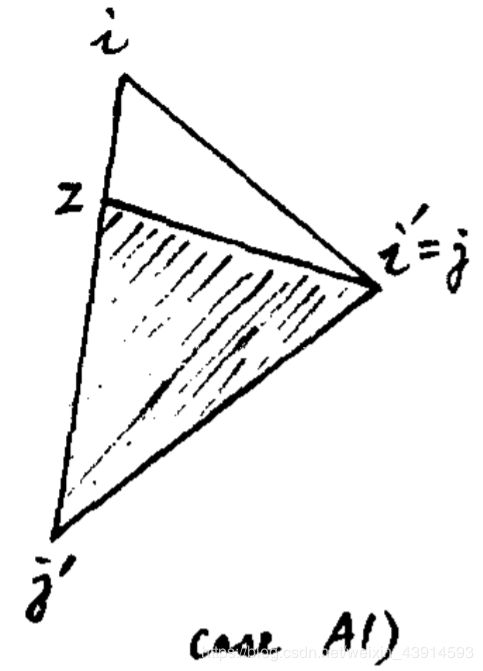
当 i = i ′ i = i' i=i′或 j = j ′ j = j' j=j′时(6-3)显然成立,下面考虑另外2个情况:A). i < i ′ = j < j ′ i < i' = j < j' i<i′=j<j′和B). i < i ′ < j < j ′ i < i' < j < j' i<i′<j<j′。
case A). i < i’ = j < j’
代入公式(6-3),得到一个“反”三角形不等式(图4的三角形 i j j ′ ijj' ijj′,两边的和小于第三边):
c ( i , j ) + c ( j , j ′ ) ≤ c ( i , j ′ ) c(i, j) + c(j, j') ≤ c(i, j') c(i,j)+c(j,j′)≤c(i,j′) i < j < j ′ i < j < j' i<j<j′ ( 6 − 4 ) (6-4) (6−4)
现在证明公式(6-4)。
假设 c ( i , j ′ ) c(i, j') c(i,j′)在 k = z k = z k=z处有最小值,即 c ( i , j ′ ) = c z ( i , j ′ ) c(i, j') = c_z(i, j') c(i,j′)=cz(i,j′)。这里定义 c k ( i , j ) c_k(i, j) ck(i,j)等于 w ( i , j ) + c ( i , k − 1 ) + c ( k , j ) w(i, j) + c(i, k-1) + c(k, j) w(i,j)+c(i,k−1)+c(k,j)。
有2个对称情况A1)和A2)。
case A1). z ≤ j
z z z是 ( i , j ′ ) (i, j') (i,j′)区间的最优点,不是 ( i , j ) (i, j) (i,j)区间的最优点,所以有:
c ( i , j ) ≤ c z ( i , j ) = w ( i , j ) + c ( i , z − 1 ) + c ( z , j ) c(i, j) ≤ c_z(i, j) = w(i, j) + c(i, z-1) + c(z, j) c(i,j)≤cz(i,j)=w(i,j)+c(i,z−1)+c(z,j)
在两边加上 c ( j , j ′ ) c(j, j') c(j,j′):
c ( i , j ) + c ( j , j ′ ) ≤ w ( i , j ) + c ( i , z − 1 ) + c ( z , j ) + c ( j , j ′ ) c(i, j) + c(j, j') ≤ w(i, j) + c(i, z-1) + c(z, j) + c(j, j') c(i,j)+c(j,j′)≤w(i,j)+c(i,z−1)+c(z,j)+c(j,j′)
≤ w ( i , j ′ ) + c ( i , z − 1 ) + c ( z , j ′ ) ≤ w(i, j') + c(i, z-1) + c(z, j') ≤w(i,j′)+c(i,z−1)+c(z,j′)
= c ( i , j ′ ) = c(i, j') =c(i,j′)
上面的推导时利用了下面2条:
1) w w w的单调性,有 w ( i , j ) ≤ w ( i , j ′ ) w(i, j)≤ w(i, j') w(i,j)≤w(i,j′) ;
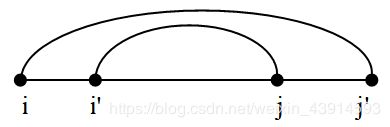
2)公式(6-4)的归纳假设:假设 z ≤ j ≤ j ′ z ≤ j ≤ j' z≤j≤j′时成立,递推出 i < j < j ′ i < j < j' i<j<j′时公式(6-4)也成立。观察下面的图,有 c ( z , j ) + c ( j , j ′ ) ≤ c ( z , j ′ ) c(z, j) + c(j, j') ≤ c(z, j') c(z,j)+c(j,j′)≤c(z,j′),它满足反三角形不等式。
case A2). z ≥ j z ≥ j z≥j。是A1)的对称情况。
case B). i < i ′ < j < j ′ i < i' < j < j' i<i′<j<j′
假设公式(6-3)右边的小区间 c ( i ′ , j ) c(i', j) c(i′,j)和大区间 c ( i , j ′ ) c(i, j') c(i,j′)分别在 k = y k = y k=y和 k = z k = z k=z处有最小值,记为:
c ( i ′ , j ) = c y ( i ′ , j ) c(i', j) = c_y(i', j) c(i′,j)=cy(i′,j)
c ( i , j ′ ) = c z ( i , j ′ ) c(i, j') = c_z(i, j') c(i,j′)=cz(i,j′)
同样有2个对称情况B1)和B2)。
case B1). z ≤ y z ≤ y z≤y
有 c ( i ′ , j ′ ) ≤ c y ( i ′ , j ′ ) c(i', j') ≤ c_y(i', j') c(i′,j′)≤cy(i′,j′)
和 c ( i , j ) ≤ c z ( i , j ) c(i, j) ≤ c_z(i, j) c(i,j)≤cz(i,j)
两式相加得:
c ( i , j ) + c ( i ′ , j ′ ) c(i, j) + c(i', j') c(i,j)+c(i′,j′)
≤ c z ( i , j ) + c y ( i ′ , j ′ ) ≤ c_z(i, j) + c_y(i', j') ≤cz(i,j)+cy(i′,j′)
= w ( i , j ) + w ( i ′ , j ′ ) + c ( i , z − 1 ) + c ( z , j ) + c ( i ′ , y − 1 ) + c ( y , j ′ ) = w(i, j) + w(i', j') + c(i, z-1) + c(z, j) + c(i', y-1) + c(y, j') =w(i,j)+w(i′,j′)+c(i,z−1)+c(z,j)+c(i′,y−1)+c(y,j′) ( 6 − 5 ) (6-5) (6−5)
公式(6-5)的进一步推导利用了下面2条:
1)根据 w w w的四边形不等式,有 w ( i , j ) + w ( i ′ , j ′ ) ≤ w ( i ′ , j ) + w ( i , j ′ ) w(i, j) + w(i', j') ≤ w(i', j) + w(i, j') w(i,j)+w(i′,j′)≤w(i′,j)+w(i,j′);
2)根据公式(6-3)的归纳假设,即假设 z ≤ y < j < j ′ z ≤ y < j < j' z≤y<j<j′时成立。观察下图,有 c ( z , j ) + c ( y , j ′ ) ≤ c ( y , j ) + c ( z , j ′ ) c(z, j) + c(y, j') ≤ c(y, j) + c(z, j') c(z,j)+c(y,j′)≤c(y,j)+c(z,j′),满足反四边形不等式。
则公式(6-5)变为:
c ( i , j ) + c ( i ′ , j ′ ) c(i, j) + c(i', j') c(i,j)+c(i′,j′)
≤ w ( i ′ , j ) + w ( i , j ′ ) + c ( i , z − 1 ) + c ( i ′ , y − 1 ) + c ( y , j ) + c ( z , j ′ ) ≤ w(i', j) + w(i, j') + c(i, z-1) + c(i', y-1) + c(y, j) + c(z, j') ≤w(i′,j)+w(i,j′)+c(i,z−1)+c(i′,y−1)+c(y,j)+c(z,j′)
≤ c y ( i ′ , j ) + c z ( i , j ′ ) ≤ c_y(i', j) + c_z(i, j') ≤cy(i′,j)+cz(i,j′)
= c ( i ′ , j ) + c ( i , j ′ ) = c(i', j) + c(i, j') =c(i′,j)+c(i,j′)
case B2). z ≥ y z ≥ y z≥y。是B1)的对称情况。
引理1证毕。
(2)证明引理2
用 K c ( i , j ) K_c(i, j) Kc(i,j)表示 m a x { k ∣ c k ( i , j ) = c ( i , j ) } max\{k|c_k(i, j) = c(i, j)\} max{k∣ck(i,j)=c(i,j)},也就是使 c ( i , j ) c(i, j) c(i,j)得到最小值的那些 k k k中,最大的那个是 K c ( i , j ) K_c(i, j) Kc(i,j)。定义 K c ( i , i ) = i K_c(i, i)=i Kc(i,i)=i。 K c ( i , j ) K_c(i, j) Kc(i,j)就是前面例子中的 s [ i ] [ j ] s[i][j] s[i][j]。
引理2: K c ( i , j ) ≤ K c ( i , j + 1 ) ≤ K c ( i + 1 , j + 1 ) K_c(i, j) ≤ K_c(i, j+1) ≤ K_c(i+1, j+1) Kc(i,j)≤Kc(i,j+1)≤Kc(i+1,j+1) ( 6 − 6 ) (6-6) (6−6)
下面是证明。
i = j i = j i=j时显然成立,下面假设 i < j i < j i<j。
先证明公式(6-6)的第一部分 K c ( i , j ) ≤ K c ( i , j + 1 ) K_c(i, j) ≤ K_c(i, j+1) Kc(i,j)≤Kc(i,j+1)。这等价于证明:对于 i < k ≤ k ′ ≤ j i < k ≤ k' ≤ j i<k≤k′≤j,有
c k ′ ( i , j ) ≤ c k ( i , j ) ⇒ c k ′ ( i , j + 1 ) ≤ c k ( i , j + 1 ) c_{k'}(i, j) ≤ c_k(i, j) \Rightarrow c_{k'}(i, j+1) ≤ c_k(i, j+1) ck′(i,j)≤ck(i,j)⇒ck′(i,j+1)≤ck(i,j+1) ( 6 − 7 ) (6-7) (6−7)
公式(6-7)的意思是:如果 c k ′ ( i , j ) ≤ c k ( i , j ) c_{k'}(i, j) ≤ ck(i, j) ck′(i,j)≤ck(i,j)成立,那么 c k ′ ( i , j + 1 ) ≤ c k ( i , j + 1 ) c_{k'}(i, j+1) ≤ c_k(i, j+1) ck′(i,j+1)≤ck(i,j+1)也成立。 c k ′ ( i , j ) ≤ c k ( i , j ) c_{k'}(i, j) ≤ c_k(i, j) ck′(i,j)≤ck(i,j)的含义是,在 [ i , j ] [i, j] [i,j]区间, k ′ k' k′是比 k k k更好的分割点,可以把 k ′ k' k′看成 [ i , j ] [i, j] [i,j]的最优分割点。扩展到区间 [ i , j + 1 ] [i, j+1] [i,j+1]时,有 c k ′ ( i , j + 1 ) ≤ c k ( i , j + 1 ) c_{k'}(i, j+1) ≤ c_k(i, j+1) ck′(i,j+1)≤ck(i,j+1),即 k ′ k' k′仍然是比 k k k更好的分割点。也就是说,区间 [ i , j + 1 ] [i, j+1] [i,j+1]的最优分割点肯定大于等于 k ′ k' k′。
下面证明公式(6-7)。
根据四边形不等式,在 k ≤ k ′ ≤ j < j + 1 k ≤ k' ≤ j < j+1 k≤k′≤j<j+1时,有
c ( k , j ) + c ( k ′ , j + 1 ) ≤ c ( k ′ , j ) + c ( k , j + 1 ) c(k, j) + c(k', j+1) ≤ c(k', j) + c(k, j+1) c(k,j)+c(k′,j+1)≤c(k′,j)+c(k,j+1)
在两边加上 w ( i , j ) + w ( i , j + 1 ) + c ( i , k − 1 ) + c ( i , k ′ − 1 ) w(i, j) + w(i, j+1) + c(i, k-1) + c(i, k'-1) w(i,j)+w(i,j+1)+c(i,k−1)+c(i,k′−1),得:
c k ( i , j ) + c k ′ ( i , j + 1 ) ≤ c k ′ ( i , j ) + c k ( i , j + 1 ) c_k(i, j) + c_{k'}(i, j+1) ≤ c_{k'}(i, j) + c_k(i, j+1) ck(i,j)+ck′(i,j+1)≤ck′(i,j)+ck(i,j+1)
把ck(i, j) 移到右边: c k ′ ( i , j + 1 ) ≤ c k ′ ( i , j ) + c k ( i , j + 1 ) − c k ( i , j ) c_{k'}(i, j+1) ≤ c_{k'}(i, j) + c_k(i, j+1) -c_k(i, j) ck′(i,j+1)≤ck′(i,j)+ck(i,j+1)−ck(i,j) ( 6 − 8 ) (6-8) (6−8)
把(6-7)的 c k ′ ( i , j ) ≤ c k ( i , j ) c_{k'}(i, j) ≤ c_k(i, j) ck′(i,j)≤ck(i,j)的两边加上 c k ( i , j + 1 ) c_k(i, j+1) ck(i,j+1):
c k ′ ( i , j ) + c k ( i , j + 1 ) ≤ c k ( i , j ) + c k ( i , j + 1 ) c_{k'}(i, j)+ c_k(i, j+1) ≤ c_k(i, j)+ c_k(i, j+1) ck′(i,j)+ck(i,j+1)≤ck(i,j)+ck(i,j+1)
c k ′ ( i , j ) + c k ( i , j + 1 ) − c k ( i , j ) ≤ c k ( i , j + 1 ) c_{k'}(i, j)+ c_k(i, j+1) - c_k(i, j) ≤ c_k(i, j+1) ck′(i,j)+ck(i,j+1)−ck(i,j)≤ck(i,j+1)
结合(6-8),得 c k ′ ( i , j + 1 ) ≤ c k ( i , j + 1 ) c_{k'}(i, j+1) ≤ c_k(i, j+1) ck′(i,j+1)≤ck(i,j+1),公式(6-7)成立。
同样可以证明,公式(6-6)的右半部分 K c ( i , j + 1 ) ≤ K c ( i + 1 , j + 1 ) K_c(i, j+1) ≤ K_c(i+1, j+1) Kc(i,j+1)≤Kc(i+1,j+1),在 i < i + 1 ≤ k ≤ k ′ i < i+1≤ k ≤ k' i<i+1≤k≤k′时成立。
引理2说明当 i 、 j i、j i、j增大时, K c ( i , j ) K_c(i, j) Kc(i,j)是非递减的。
(3)证明四边形不等式定理
利用引理2,可推论出四边形不等式定理,即用DP计算所有的 c ( i , j ) c(i, j) c(i,j)的时间复杂度是 O ( n 2 ) O(n^2) O(n2)的。下面对这一结论进行说明。
用DP计算 c ( i , j ) c(i, j) c(i,j)时,是按 δ = j − i = 0 , 1 , 2 , . . . , n − 1 \delta= j - i = 0, 1, 2, ..., n-1 δ=j−i=0,1,2,...,n−1的间距逐步增加进行递推计算的。具体过程请回顾前面第2节求dp[i][j]的代码。从 c ( i , j ) c(i, j) c(i,j)递推到 c ( i , j + 1 ) c(i, j+1) c(i,j+1)时,只需要 K c ( i + 1 , j + 1 ) − K c ( i , j ) K_c(i+1, j+1) - K_c(i, j) Kc(i+1,j+1)−Kc(i,j)次最少限度的操作就够了。总次数是多少呢?对一个固定的 δ \delta δ,计算所有的 c ( i , j ) , 1 ≤ i ≤ n − δ , j = i + δ c(i, j),1≤ i ≤ n-\delta,j = i+\delta c(i,j),1≤i≤n−δ,j=i+δ,次数是:
i = 1时: K c ( 1 + 1 , 1 + δ + 1 ) − K c ( 1 , δ + 1 ) = K c ( 2 , δ + 2 ) − K c ( 1 , δ + 1 ) K_c(1+1, 1+\delta+1) - K_c(1, \delta+1) = K_c(2, \delta+2) - K_c(1, \delta+1) Kc(1+1,1+δ+1)−Kc(1,δ+1)=Kc(2,δ+2)−Kc(1,δ+1)
i = 2时: K c ( 2 + 1 , 2 + δ + 1 ) − K c ( 2 , δ + 2 ) = K c ( 3 , δ + 3 ) − K c ( 2 , δ + 2 ) K_c(2+1, 2+\delta+1) - K_c(2, \delta+2) = K_c(3, \delta+3) - K_c(2, \delta+2) Kc(2+1,2+δ+1)−Kc(2,δ+2)=Kc(3,δ+3)−Kc(2,δ+2)
i = 3时: K c ( 3 + 1 , 3 + δ + 1 ) − K c ( 3 , δ + 3 ) = K c ( 4 , δ + 4 ) − K c ( 3 , δ + 3 ) K_c(3+1, 3+\delta+1) - K_c(3, \delta+3) = K_c(4, \delta+4) - K_c(3,\delta+3) Kc(3+1,3+δ+1)−Kc(3,δ+3)=Kc(4,δ+4)−Kc(3,δ+3)
…
i = n − δ i = n-\delta i=n−δ时: K c ( n − δ + 1 , n − δ + δ + 1 ) − K c ( n − δ , δ + n − δ ) = K c ( n − δ + 1 , n + 1 ) − K c ( n − δ , n ) K_c(n-\delta+1, n-\delta+\delta+1) - K_c(n-\delta, \delta+n-\delta) = K_c(n-\delta+1, n+1) - K_c(n-\delta, n) Kc(n−δ+1,n−δ+δ+1)−Kc(n−δ,δ+n−δ)=Kc(n−δ+1,n+1)−Kc(n−δ,n)
以上式子相加,次数 = K c ( n − δ + 1 , n + 1 ) − K c ( 1 , δ + 1 ) = K_c(n-\delta+1, n+1) - K_c(1, \delta+1) =Kc(n−δ+1,n+1)−Kc(1,δ+1),小于 n n n。
对一个 δ \delta δ,计算次数是 O ( n ) O(n) O(n)的;有 n n n个 δ \delta δ,总计算复杂度是 O ( n 2 ) O(n^2) O(n2)的。
以上证明了四边形不等式定理。
(4) m i n min min和 m a x max max
前面讨论的都是 m i n min min,如果是 m a x max max,也可以进行四边形不等式优化。此时四边形不等式是“反”的:
w ( i , j ) + w ( i ′ , j ′ ) ≥ w ( i ′ , j ) + w ( i , j ′ ) w(i, j) + w(i', j') ≥ w(i', j) + w(i, j') w(i,j)+w(i′,j′)≥w(i′,j)+w(i,j′) i ≤ i ′ ≤ j ≤ j ′ i ≤ i' ≤ j ≤ j' i≤i′≤j≤j′
定义:
c ( i , j ) = w ( i , j ) + m a x ( a ( i , k ) + b ( k , j ) ) c(i, j) = w(i, j) + max(a(i, k) + b(k, j)) c(i,j)=w(i,j)+max(a(i,k)+b(k,j)) i ≤ k ≤ j i ≤ k ≤ j i≤k≤j
引理3:若 w 、 a 、 b w、a、b w、a、b都满足反四边形不等式,那么 c c c也满足反四边形不等式。
引理4:如果 a a a和 b b b满足反四边形不等式,那么:
K c ( i , j ) ≤ K c ( i , j + 1 ) ≤ K c ( i + 1 , j + 1 ) K_c(i, j) ≤ K_c(i, j+1) ≤ K_c(i+1, j+1) Kc(i,j)≤Kc(i,j+1)≤Kc(i+1,j+1) i ≤ j i ≤ j i≤j
证明与引理1和引理2的证明类似。
7 一维决策单调性优化
上述的四边形不等式优化,是“二维决策单调性”优化。在“一维决策单调性”的情况下也能优化。
李煜东《算法竞赛进阶指南》“0x5B四边形不等式”指出:状态转移方程 F [ i ] = m i n 0 ≤ j < i { F [ j ] + v a l ( j , i ) } F[i] = min_{0≤j
8 例题
拿到题目后,先判断w是否单调、是否满足四边形不等式,再使用四边形不等式优化DP。
8.1 石子合并
洛谷 P1880 https://www.luogu.com.cn/problem/P1880
题目描述:在一个圆形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N 堆石子合并成1堆的最小得分和最大得分。
输入:
数据的第 1 行是正整数 N,表示有 N 堆石子。
第 2 行有 N 个整数,第 i 个整数 ai表示第 i 堆石子的个数。
输出:
输出共 2 行,第 1 行为最小得分,第 2 行为最大得分。
样例输入:
4
4 5 9 4
样例输出:
43
54
题解:
(1)如果石子堆没有顺序,可以任意合并,用贪心法,每次选择最小的两堆合并。
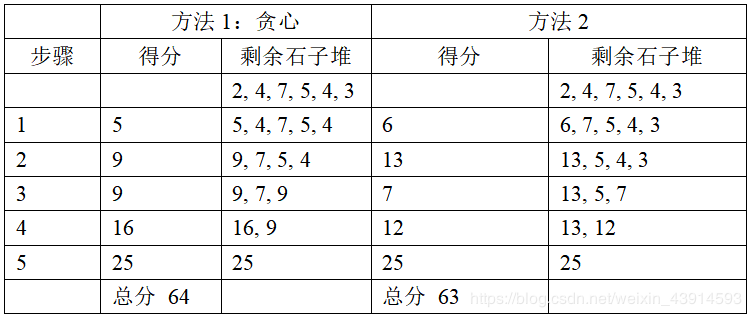
(2)本题要求只能合并相邻的两堆,不能用贪心法。贪心操作是每次合并时找石子数相加最少的两堆相邻石子。例如环形石子堆开始是{2, 4, 7, 5, 4, 3},下面用贪心得到最小值64,但是另一种方法得到63。
(3)用四边形优化DP求解石子合并的最小值,复杂度是 O ( n 2 ) O(n^2) O(n2)。
状态转移矩阵 d p [ i ] [ j ] dp[i][j] dp[i][j]前文已有说明,这里不再赘述。
最小值用四边形不等式优化DP, w w w在四边形不等式中取等号: w [ i ] [ j ] + w [ i ′ ] [ j ′ ] = w [ i ] [ j ′ ] + w [ i ′ ] [ j ] w[i][j] + w[i'][j'] = w[i][j'] + w[i'][j] w[i][j]+w[i′][j′]=w[i][j′]+w[i′][j]。
本题的石子堆是环状的,转换为线形的更方便处理。复制和原来一样的数据,头尾接起来,使 n n n的数列转化为 2 n 2n 2n的数列,变成线形的。
(4)这一题除了求最小值,还求最大值。虽然最大值也用DP求解,但是它不满足反四边形不等式的单调性要求,不能优化。而且也没有必要优化,可以用简单的推理得到:区间 [ i , j ] [i, j] [i,j]的最大值,等于区间 [ i , j − 1 ] [i, j-1] [i,j−1]和 [ i + 1 , j ] [i+1, j] [i+1,j]中的最大值加上 w ( i , j ) w(i, j) w(i,j)。
(5)石子合并问题的最优解法是GarsiaWachs算法,复杂度O(nlogn)。读者可以参考“洛谷P5569 石子合并”,这题 N ≤ 40000 N ≤ 40000 N≤40000,用DP会超时。
8.2 最优二叉搜索树
最优二叉搜索树是Knuth(高纳德)解决的经典问题,是四边形不等式优化的起源。
Optimal Binary Search Tree
uva10304 https://vjudge.net/problem/UVA-10304
题目描述:给定 n n n个不同元素的集合 S = ( e 1 , e 2 , . . . , e n ) S =(e_1, e_2, ..., e_n) S=(e1,e2,...,en),有 e 1 < e 2 < . . . < e n e_1 < e_2 < ... < e_n e1<e2<...<en,把 S S S的元素建一棵二叉搜索树,希望查询频率越高的元素离根越近。
访问树中元素 e i e_i ei的成本 c o s t ( e i ) cost(e_i) cost(ei)等于从根到该元素结点的路径边数。给定元素的查询频率 f ( e 1 ) , f ( e 2 ) , . . . , f ( e n ) f(e_1),f(e_2),...,f(e_n) f(e1),f(e2),...,f(en),定义一棵树的总成本是:
f ( e 1 ) ∗ c o s t ( e 1 ) + f ( e 2 ) ∗ c o s t ( e 2 ) + . . . + f ( e n ) ∗ c o s t ( e n ) f(e_1) ∗cost(e_1) + f(e_2) ∗cost(e_2) + ... + f(e_n) ∗ cost(e_n) f(e1)∗cost(e1)+f(e2)∗cost(e2)+...+f(en)∗cost(en)
总成本最低的树就是最优二叉搜索树。
输入:
输入包含多个实例,每行一个。每行以 1 ≤ n ≤ 250 1≤n≤250 1≤n≤250开头,表示 S S S的大小。在 n n n之后,在同一行中,有 n n n个非负整数,它们表示元素的查询频率, 0 ≤ f ( e i ) ≤ 100 0 ≤ f(e_i) ≤ 100 0≤f(ei)≤100。
输出:
对于输入的每个实例,输出一行,打印最优二叉搜索树的总成本。
样例输入:
1 5
3 10 10 10
3 5 10 20
样例输出:
0
20
20
题解:
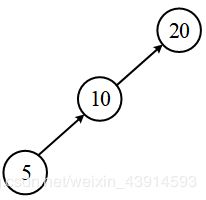
二叉搜索树(BST)的特点是每个结点的值,比它的左子树上所有结点的值大,比右子树上所有值小。二叉搜索树的中序遍历,是从小到大的排列。第3个样例的最优二叉搜索树的形状见下图,它的总成本是 5 ∗ 2 + 10 ∗ 1 = 20 5*2+10*1=20 5∗2+10∗1=20。
题目给的元素已经按照从小到大排列,可以方便地组成一棵BST。
设 d p [ i ] [ j ] dp[i][j] dp[i][j]是区间 [ i , j ] [i, j] [i,j]的元素组成的BST的最小值。把区间 [ i , j ] [i, j] [i,j]分成两部分 [ i , k − 1 ] [i, k-1] [i,k−1]和 [ k + 1 , j ] [k+1, j] [k+1,j], k k k在 i i i和 j j j之间滑动。用区间 [ i , j ] [i, j] [i,j]建立的二叉树, k k k是根结点。这是典型的区间DP,状态转移方程:
d p [ i ] [ j ] = m i n { d p [ i ] [ k − 1 ] + d p [ k + 1 ] [ j ] + w ( i , j ) − e [ k ] } dp[i][j] = min\{dp[i][k-1] + dp[k+1][j] + w(i, j) - e[k]\} dp[i][j]=min{dp[i][k−1]+dp[k+1][j]+w(i,j)−e[k]}
w ( i , j ) w(i, j) w(i,j)是区间和, w ( i , j ) = f i + f i + 1 + . . . + f j w(i, j) = f_i +f_{i+1}+...+ f_j w(i,j)=fi+fi+1+...+fj。当把两棵左右子树连在根结点上时,本身的深度增加 1 1 1,所以每个元素都多计算一次,这样就解决了 c o s t ( e i ) cost(e_i) cost(ei)的计算。最后,因为根节点 k k k的层数是0,所以减去根节点的值 e [ k ] e[k] e[k]。
w(i, j)符合四边形不等式优化的条件,所以 d p [ i ] [ j ] dp[i][j] dp[i][j]可以用四边形不等式优化。
8.3 其他题目
很多区间DP问题都能用四边形不等式优化。
hdu 3516 Tree Construction http://acm.hdu.edu.cn/showproblem.php?pid=3516
hdu 2829 Lawrence http://acm.hdu.edu.cn/showproblem.php?pid=2829
hdu 3506 Monkey Party http://acm.hdu.edu.cn/showproblem.php?pid=3506
洛谷P1912 诗人小G https://www.luogu.com.cn/problem/P1912
洛谷 P4767 邮局 < https://www.luogu.com.cn/problem/P4767>
HDU 3480 Division http://acm.hdu.edu.cn/showproblem.php?pid=3480
Donald E. Knuth. Optimum binary search trees. Acta Informatica, 1:14–25, 1971. ↩︎
F. Frances Yao. Efficient dynamic programming using quadrangle inequalities. In Proceedings of the 12th Annual ACM Symposium on Theory of Computing, pages 429–435, 1980.
论文下载:http://www.cs.ust.hk/mjg_lib/bibs/DPSu/DPSu.Files/p429-yao.pdf ↩︎参考《算法竞赛入门到进阶》7.3节 区间DP,“石子合并”问题。 ↩︎
读者可以自己证明。证明过程参考《算法竞赛进阶指南》李煜东,河南电子音像出版社,329页,“0x5B 四边形不等式”。 ↩︎