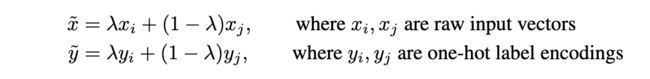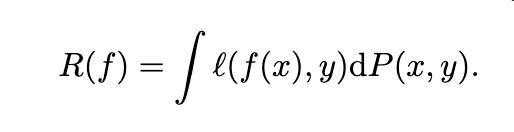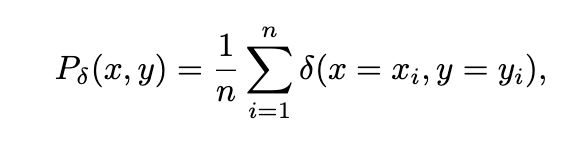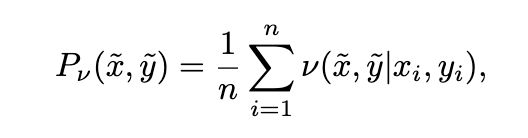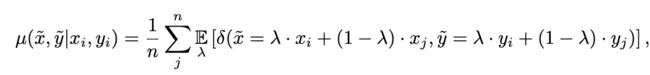一种图像增广(Image Augmentation)方式 Mix Up 算法 附有代码解析
这是对facebook研究团队的一篇文章 Mixup: Beyond Empirical Risk Minimization 的解读
这篇文章相对于之前提到的Sample pariring来说就不那么神奇了,因为毕竟文章作者在里面有一些相关理论的推导。文章开头通篇讲的是ERM也就是经验风险最小化原则是整个机器学习遵循的原则,作者正是基于此思想才提出了MixUp的方法。在一般的机器学习任务中,比如分类任务中,对于ERM原则遵循的一种变种被称之为相邻风险最小化(Vicinal Risk Minimization),VRM实际上是指在训练集周围的邻域内构造一些样本参与训练来扩大原先的训练数据集的分布,通常情况下认为这些围绕着训练集某个类别而扩展的邻域和该类别数据是同属一类,并且不研究不同类别样本的邻域之间的关系(这里我的理解是,VRM原则是将原来的训练集进行邻域扩充,但是某个类别的邻域从属于某个类别,即使是该邻域同另一个邻域有相交的地方,但也不研究这些相交区域到底该如何规划)。
基于上述思想,作者提出混合思路:
如上式所述,输入样本x进行混合,得到一个新的样本,于此同时对该样本的标签也按照这样的混合方式进行混合,这样相当于用线性的方式获得一个原训练集某个类别样本的邻域。我通过对这篇文章代码的研究,实际上作者是这样操作的:
1. 利用上述公式,将训练集中某一数据选出x_i,然后随机选出数据x_j,两者按照上述公式进行合成,于此同时标签也按照上述公式合成,并且同时可以得到合成用的比例
2. 将这种合成数据送入网络,获得网络的输出
3. 将输送入loss函数进行计算,但是注意此时的loss函数是合成loss,是由y_i和y_j合成的,loss计算分为两部分,先计算模型预测同y_i的loss,然后乘以第一步获得的比例,然后模型预测同y_j计算loss,乘以1减去第一步获得的比例,两者求和
如下是代码解析:
def mixup_data(x, y, alpha=1.0, use_cuda=True):
# 对数据的mixup 操作 x = lambda*x_i+(1-lamdda)*x_j
'''Returns mixed inputs, pairs of targets, and lambda'''
if alpha > 0:
lam = np.random.beta(alpha, alpha)
else:
lam = 1
batch_size = x.size()[0]
if use_cuda:
index = torch.randperm(batch_size).cuda()
else:
index = torch.randperm(batch_size)
mixed_x = lam * x + (1 - lam) * x[index, :] # 此处是对数据x_i 进行操作
y_a, y_b = y, y[index] # 记录下y_i 和y_j
return mixed_x, y_a, y_b, lam # 返回y_i 和y_j 以及lambda
def mixup_criterion(criterion, pred, y_a, y_b, lam):
# 对loss函数进行混合,criterion是crossEntropy函数
return lam * criterion(pred, y_a) + (1 - lam) * criterion(pred, y_b)
def train(epoch):
print('\nEpoch: %d' % epoch)
net.train()
train_loss = 0
reg_loss = 0
correct = 0
total = 0
for batch_idx, (inputs, targets) in enumerate(trainloader):
if use_cuda:
inputs, targets = inputs.cuda(), targets.cuda()
inputs, targets_a, targets_b, lam = mixup_data(inputs, targets,
args.alpha, use_cuda) # 对数据集进行mixup操作
inputs, targets_a, targets_b = map(Variable, (inputs,
targets_a, targets_b))
outputs = net(inputs)
loss = mixup_criterion(criterion, outputs, targets_a, targets_b, lam) #对loss#函数进行mixup操作
train_loss += loss.data[0]
_, predicted = torch.max(outputs.data, 1)
total += targets.size(0)
correct += (lam * predicted.eq(targets_a.data).cpu().sum().float()
+ (1 - lam) * predicted.eq(targets_b.data).cpu().sum().float())
我说这篇文章好就好在后面作者给出了一定的数学解释,现在看数学原理:
假定数据x和标签y,并且这两者具有联合分布P(x,y) (当然这个联合分布函数是未知的), 模型函数用f表示,loss函数用l表示,则经验风险为
通常情况下我们的训练集{x,y}可以用狄拉克函数来表示,假定训练集足够,可以模拟真实情况,那么上述的P可以用狄拉克函数近似,如下
那么上述表达式带入第一个式子,可得
到此为止就是在正常的未经增广的训练数据集下的ERM表达式,那么先前已经提到VRM来做图像增广的思想,那么回到这个式子上P就不应该是一个狄拉克函数的表示,而是服从邻域分布v的一种表达,P的表达式可由上述第二个式子退化为:
这里的v是邻域分布函数,同样的上述第三个式子可以退化为:
注意,由于数据发生了增广,因而这里的数据量由最开始的n变为m。
而这篇文章提出的mixup 方法实际上就是提出了一种上述的v式子,即一种线性表达来代替上述第4个式子中的v
到这里便是mixup的数学解释。
从模型训练定性的角度来说,mixup相当于让模型在不同类别之间学会一种线性的过度,这样会导致模型在预测过程中不容易在某些类别之间发送震荡,这一点从文章实验的权重稳定性可以看得出
从我本人实验结果的角度来说,确实可以按照上述定性解释这样理解;不过这实际上给我们提供了一种思路,就是说在分类任务中的数据增广的实质有可能是打通孤立数据样本之间的联系,这种联系有可能是一种线性关系,也有可能是另一种非线性关系,模型所要做的是学会如何在已有这些联系的基础上的判别能力,这样可以保证模型不发生过拟合,也就是文章中提到的震荡。