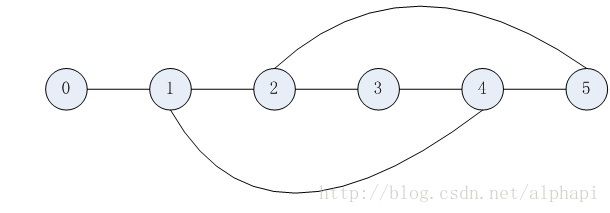
计算无向无权图中两点间所有的最短路径

 

一、例子

如上图，节点0到节点5的最短路径长度为3，有两条最短路径：

路径1：0 — 1 — 4— 5

路径2：0 — 1 — 2— 5

二、相关名称

tempLadder：             存储当前正在计算的路径
canditStack：              存储备选结点的栈
shortestLength：        最短路径长度
startNode：                开始节点
endNode：                 终止节点
allShortestPath：    存储startNod与endNode之间的所有的最短路径。

三、约束条件：
1、如果节点node_a在路径tempLadder中，从startNode起，node_a之前的各节点与node_a的距离分别是i,i-1,i-2....1，node_a与终结点的距离为shortestLength-i。

2、遍历与node_a相邻的各个节点，如果结点node_i已经在当前路径tempLadder或者在canditStack中，或者与endNode的距离大于node_a与endNode的距离，则应该过滤掉node_i。

四：算法过程：
step1、使用floyd计算结点间的最短距离

step2、输入起点和终点的结点序号

step3、计算起点到终点间的所有最短距离

step3.1
 将startNode加入到tempLadder中，再将所有与startNode距离为1，与终结点距离为shortestLength-1的结点加入canditStack中，然后进入step3.2。

step3.2
当canditStack为空时，进入step4。

当canditStack不为空时，从canditStack中取出栈顶元素node，然后进入step3.3。

 

step3.3

如果node满足条件1，则加入到tempLadder中，如果node与endNode距离为1，则同时将tempLadder加入到allShortestPath，tempLadder进行出栈，然后进入step3.4。

如果node不满足条件1，tempLadder出栈，直到node满足条件1为止，然后将node压入tempLadder中，然后进入step3.4。

 

step3.4

遍历与node距离为1的节点，如果满足条件2，则过滤掉，否则，加入到canditStack中，进入step3.2。

 

step4

算法终止。

 

五、程序

////////////////////////allshortpath.h////////////////////////////////
#ifndef H_FLOYD
#define H_FLOYD


#include 


using namespace std;


#define MAX 1000
#define NODECOUNT 6  //结点数


typedef char VexType;


struct GraphMatrix
{
int n; //图的顶点个数
VexType *vexs;//顶点信息
int arcs[NODECOUNT][NODECOUNT];//边信息
};


struct ShortPath
{
int a[NODECOUNT][NODECOUNT];
int nextvex[NODECOUNT][NODECOUNT];
};


void floyd(GraphMatrix * pgraph, ShortPath * ppath);


void show_GraphMatirx(GraphMatrix * pgraph, int nodeCount);


void show_path(ShortPath * ppath, int nodeCount);


int shortestPath_2Nodes(int startNode, int endNode, ShortPath *ppath);


//判断结点是否已经存在当前路径中
int inVector(int nodeNum, vector & tempvector, ShortPath *ppath);


int isPostNode(int nodeNum, int endNode, vector & tempvector, ShortPath *ppath);


vector> getAllShortestPath(int startNode, int endNode, ShortPath *ppath, int nodeCount);


#endif

/////////////////////////////////////////allshortpath.cpp//////////////////////////////////////////////
#include 
#include 
#include 
#include 


#include "allshortpath.h"


void floyd(GraphMatrix * pgraph, ShortPath * ppath)
{
int i,j,k;
for ( i=0; in; i++ )
{
for ( j=0; jn; j++ )
{
ppath->a[i][j] = pgraph->arcs[i][j];
}
}


for ( k=0; kn; k++ )
{
for ( i=0; in; i++ )
{
for ( j=0; jn; j++ )
{
if ( (ppath->a[i][k]>=MAX)||(ppath->a[k][j]>=MAX) )
continue;


if ( ppath->a[i][j] > (ppath->a[i][k] + ppath->a[k][j]) )
{
ppath->a[i][j] = ppath->a[i][k] + ppath->a[k][j];
}
}
}
}
}


void show_GraphMatirx(GraphMatrix *pgraph, int nodeCount)
{
int i,j;


for ( i=0; iarcs[i][j]);
}
printf("\n");
}
printf("\n");
}


void show_path(ShortPath *ppath, int nodeCount)
{
int i, j;


for ( i=0; ia[i][j]);
}
printf("\n");
}
printf("\n");
}


int shortestPath_2Nodes(int startNode, int endNode, ShortPath *ppath)
{
int distance = ppath->a[startNode][endNode];
return distance;
}


vector> getAllShortestPath(int startNode, int endNode, ShortPath *ppath, int nodeCount)
{
int nodeNum = 0;
int tempFromStack;
int tempFromLadder;
int shortestLength;


vector canditNodeStack;
vector tempLadder;
vector> resultvector;


if ( startNode == endNode )
{
return resultvector;
}

tempLadder.push_back(startNode);
if ( ppath->a[startNode][endNode] == 1 )
{
tempLadder.push_back(endNode);
resultvector.push_back(tempLadder);
return resultvector;
}

shortestLength = shortestPath_2Nodes(startNode, endNode, ppath);


for ( nodeNum = 0; nodeNum < nodeCount; nodeNum++ )
{
if ( shortestPath_2Nodes(nodeNum, startNode, ppath) == 1 )
{
canditNodeStack.push_back(nodeNum);
}
}


while ( canditNodeStack.size() > 0 )
{
tempFromStack = canditNodeStack.back(); 
canditNodeStack.pop_back();

int d_temp_end = shortestPath_2Nodes(tempFromStack, endNode, ppath);

if ( d_temp_end == 0 && tempLadder.size() == shortestLength )
{
tempLadder.push_back(tempFromStack);
resultvector.push_back(tempLadder);
tempLadder.pop_back();
}
else
{
if ( isPostNode(tempFromStack, endNode, tempLadder, ppath) == 1 )
{
if ( tempLadder.size() <= shortestLength )
{
tempLadder.push_back(tempFromStack);
}
}
else
{
while ( tempLadder.size() > 0 && tempLadder.back() != startNode )
{
tempLadder.pop_back();


if ( isPostNode(tempFromStack, endNode, tempLadder, ppath) == 1 )
{
tempLadder.push_back(tempFromStack);
break;
}


}
}
}


for ( nodeNum = 0; nodeNum < nodeCount; nodeNum++ )
{
int i2 = shortestPath_2Nodes(tempFromStack, nodeNum, ppath); 
int i3 = shortestPath_2Nodes(endNode, nodeNum, ppath);
if ( i2 == 1 && d_temp_end > i3 && !inVector(nodeNum, canditNodeStack, ppath) && !inVector(nodeNum, tempLadder, ppath))
{
canditNodeStack.push_back(nodeNum);
}
}
}


return resultvector;


}


int inVector(int nodeNum, vector & tempvector, ShortPath *ppath)
{
int exist = 0;
vector::iterator it;
for ( it=tempvector.begin(); it!=tempvector.end(); it++ )
{


if(shortestPath_2Nodes(*it, nodeNum, ppath)==0)
{
exist = 1;
break;
}
}


return exist;


}


int isPostNode(int nodeNum, int endNode, vector & tempvector, ShortPath *ppath)
{
if ( nodeNum == tempvector.back() )
{
return 0;
}


int flag = 1;
int d_temp_end = shortestPath_2Nodes(nodeNum, endNode, ppath);
int d_back_end = shortestPath_2Nodes(tempvector.back(), endNode, ppath);


if ( d_temp_end >= d_back_end )
{
return 0;
}


for ( int i = tempvector.size() - 1; i >= 0; i-- )
{
if ( shortestPath_2Nodes(nodeNum, tempvector.at(i), ppath) != (tempvector.size() - i) )
{
flag = 0;
}


}


return flag;


}

////////////////////////main.cpp////////////////////////////////////
#include 
#include 
#include 


#include "allshortpath.h"


using namespace std;


void CalAllShortestPath()
{
int i=0;
int j=0;


GraphMatrix *pgraph = (GraphMatrix *)malloc(sizeof(struct GraphMatrix));
ShortPath   *ppath  = (ShortPath *)malloc(sizeof(struct ShortPath));


if ( pgraph==NULL || ppath==NULL )
{
return;
}


pgraph->n = NODECOUNT;


////////////////////初始化无向无权图的邻接矩阵///////////////////////////
int arcs[NODECOUNT][NODECOUNT]={0,1,MAX,MAX,MAX,MAX,  1,0,1,MAX,1,MAX,  MAX,1,0,1,MAX,1,  MAX,MAX,1,0,1,MAX,  MAX,1,MAX,1,0,1,  MAX,MAX,1,MAX,1,0};
//int arcs[POINTNUM][POINTNUM]={0,1,1,MAX,1,MAX,MAX,MAX,  1,0,1,1,MAX,MAX,MAX,MAX,  1,1,0,1,MAX,MAX,MAX,MAX,  MAX,1,1,0,MAX,1,MAX,MAX,  1,MAX,MAX,MAX,0,MAX,1,1,  MAX,MAX,MAX,1,MAX,0,1,1, MAX,MAX,MAX,MAX,1,1,0,1, MAX,MAX,MAX,MAX,1,1,1,0};

for ( i = 0; i < NODECOUNT; i++ )
{
for ( j = 0; j < NODECOUNT; j++ )
{
pgraph->arcs[i][j] = arcs[i][j];
}
}


show_GraphMatirx(pgraph, NODECOUNT);


floyd(pgraph, ppath);


show_path(ppath, NODECOUNT);
int startNode = 5;
int endNod = 0;
vector> result = getAllShortestPath(startNode, endNod, ppath, NODECOUNT);
vector eachone;
vector::iterator eachI;
set::iterator it;
vector>::iterator resultIt;


for ( resultIt=result.begin(); resultIt!=result.end(); resultIt++ )
{
eachone = *resultIt;


for ( eachI=eachone.begin(); eachI!=eachone.end(); eachI++ )
{
cout<<*eachI<<" ";
}


cout<