线性回归理论与sklearn使用回归例子

简单线性回归

算法理论

• 数据集：$(x_i,y_i，i=1,2,3,4...,n)$
• 线性模型：$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_{2}x+...$
• 模型估计：$h_{\theta }(x_i)={\theta }_0+{\theta }_1{x}_i+{\theta }_2{x}_i$
• 参数：${\theta }_i,i=0,1,2,3,4...$

模型评估

• 均方误差
  最小化误差的平方和 ，步骤如下：

1. 计算所有样本误差的平均（代价函数）,也叫均方误差（MSE）
   $$MSE=\frac{1}{m}{\sum }_{i=1}^m(\hat{y}-y{)}^2$$
2. 使用最优化方法寻找数据的最佳函数匹配

• 代价函数
  $$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

其为一个凸函数，其最低点为代价函数最小值，即参数的最优解，使性能最好。

模型参数求解

极大似然估计法

最小二乘法来源极大似然估计，是一种理论性的参数估计方法。一般步骤为：

1. 写出似然函数：所有样本误差概率相乘
2. 对似然函数取对数，并整理；将公式连乘变为连加
3. 求导数；针对θ值进行求导操作
4. 解似然方程：求出θ的最优解
   $$P\left(y_i|x_i;\theta \right)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left({\theta }^T{x}_i-y_i\right)}^2}{2{\sigma }^2}\right)$$
   $$L(\theta )=\prod _{i=1}^{m}P\left(y_i|x_i;\theta \right)$$
   $$L(\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left({\theta }^T{x}_i-y_i\right)}^2}{2{\sigma }^2}\right)$$
   $\begin{array}{rl}l(\theta )=\log L(\theta )& =\log \prod [\sum _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left({\theta }^T{x}_i-y_i\right)}^2}{2{\sigma }^2}\right)\\ & =\sum _{i=1}^m\log \left[\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left({\theta }^T{x}_i-y_i\right)}^2}{2{\sigma }^2}\right)\right]\\ & =m\log \frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{{\sigma }^2}\cdot \frac{1}{2}\sum _{i=1}^m{\left({\theta }^T{x}_i-y_i\right)}^2\end{array}$

• σ为已知值，上式极大值，而被减数是定值，所以被减数越小，整体公式数值越大
  $$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

梯度下降法

梯度下降：是一个用来求函数最小值的算法，将使用梯度下降法来求出代价函数$J({\theta }_0.{\theta }_1)$的最小值。

• 思想是：开始时随机选择一个参数组合，计算代价函数，然后寻找下一个能让代价函数值下降最多的参数组合。
• 原理：每一次都同时让所有的参数减去步长\alpha乘以代价函数的导数：

$${\theta }_j={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)$$

• 学习率（超参数）$\alpha$调参：不宜太大，不宜太小

梯度下降python实现

'''
步骤：
1、确定步长，theta的初始值
2、计算代价函数值
3、计算代价函数导数
4、更新theta参数值
'''
def GD():
    # 随机一个初始值
    init_theta = random.randint(-10, 10)
    x = init_theta
    #随机一个学习率
    alpha = (random.randint(1,999)) / 10000
    #设置迭代最大次数
    m_iter = 10
    #求解过程
    X = []  #记录生成的theta值
    Y = []  #记录代价函数值
    y = f(x)
    X.append(x)
    Y.append(y)
    y_change = 1
    i = 0
    while y_change > 1e-10 and i < m_iter:
        x -= alpha * g(x)
        pre_y,y = y,f(x)
        y_change = np.abs(pre_y - y)
        i += 1
        X.append(x)
        Y.append(y)

    min_x,max_x = np.min(X),np.max(X)
    dist = np.max([np.abs(min_x - x),np.abs(max_x - x)]) + 0.1
    min_x = x - dist
    max_x = x + dist
    X2 = np.arange(min_x,max_x,0.05)
    Y2 = list(map(lambda t:f(t),X2))
    plt.plot(X2,Y2)
    plt.plot(X,Y,'bo--')
    plt.show()

'''
3D效果显示
'''
import numpy as np
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def GD_3D():
    init_theta1 = random.randint(-10,10)
    init_theta2 = random.randint(-10,10)
    x1 = init_theta1
    x2 = init_theta2
    alpha = (random.randint(1,999)) / 10000
    max_iter = 100
    X1 = []
    X2 = []
    Y = []
    i = 0
    y = f1(x1,x2)
    X1.append(x1)
    X2.append(x2)
    Y.append(y)
    error = 1
    while error > 1e-10 and i < max_iter:
        x1 -= alpha * g_x1(x1)
        x2 -= alpha * g_x2(x2)
        pre_y,y = y,f1(x1,x2)
        error = np.abs(pre_y - y)
        i += 1
        X1.append(x1)
        X2.append(x2)
        Y.append(y)

    max_x1 = np.max(np.abs(X1))
    max_x2 = np.max(np.abs(X2))
    X12 = np.arange(-max_x1,max_x1,0.05)
    X22 = np.arange(-max_x2,max_x2,0.05)
    X12,X22 = np.meshgrid(X12,X22)
    Y2 = np.array(list(map(lambda  t:f1(t[0],t[1]),zip(X12.flatten(),X22.flatten())))).reshape(X12.shape)

    fig = plt.figure()
    ax = Axes3D(fig)
    ax.plot_surface(X12,X22,Y2,rstride=1,cstride=1,cmap='rainbow')
    ax.plot(X1,X2,Y,'ro--')
    plt.show()

多项式回归

• 线性回归的局限性是只能应用于存在线性关系的数据中，但是在实际生活中，很多数据之间是 非线性关系，也可以用线性回归拟合非线性回归，但效果很差，此时就需要对线性回归模型进 行改进，使之能够拟合非线性数据。
• 目标：将数据进行升维处理，可以更好的适应模型
  $$h_{\theta }={\theta }_0+{\theta }_1{x}_1+{\theta }_3{x}_1^{2+...}$$

正则化

• 结构风险最小化可以理解为：最小化目标函数（代价函数+正则化项）
  $$\mathrm{Obj}(w)=\frac{1}{2N}\sum _{i=1}^N{\left(w\cdot x-y_i\right)}^2+\lambda R(w)$$

正则化方法

• L1正则化 ：使用L1正则化的代价函数的回归是Lasso回归
  • 权值向量w中各个元素的绝对值之和： $$R(w)=\Vert w{\Vert }_1=\left|w_1\right|+\left|w_2\right|$$
• L2正则化 ：使用L2正则化的代价函数的回归是岭回归（Ridge回归）
  • 权值向量w中各个元素的平方和：$$R(w)=\frac{1}{2}\Vert w{\Vert }_2^2=\frac{1}{2}\left(w_1^2+w_2^2\right)$$
• L1正则化 VS L2正则化
  • L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
  • L2正则化可以防止模型过拟合（overfitting）
• 同时使用L1正则和L2正则的线性回归模型就称为Elasitc Net算法(弹性网络算法)
  $$\mathrm{Obj}(w)=\frac{1}{2N}\sum _{i=1}^N{\left(w\cdot x-y_i\right)}^2+\lambda (\mathrm{p}\mathrm{L}1+(1-\mathrm{p})\mathrm{L}2)$$

思考

为什么 L1 正则可以产生稀疏模型（很多参数=0），而 L2 正则不会出现很多参数为0的情况？

• 加入正则化项后：$Obj(w)=\frac{1}{2N}{\sum }_{i=1}^N{\left(w\cdot x-y_i\right)}^2+\lambda R(w)$
• 要让函数达到最小，通过${\min }_w\mathrm{Obj}(w)={\min }_w\frac{1}{2N}{\sum }_{i=1}^m{\left(w\cdot x-y_i\right)}^2+\lambda R(w)$，反解参数w
• ${\min }_w\frac{1}{2N}{\sum }_{i=1}^N{\left(w\cdot x-y_i\right)}^2$
  s.t. $R(w)\le t$
  
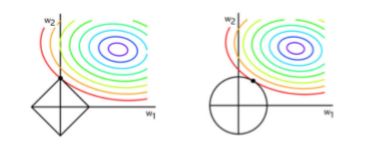
  如图： 这就把 w 的解限制在黑色区域内，同时使得经验风险尽可能小，因此取交点就是最优 解，从图可以看出，因为L1正则黑色区域是有棱角的，所以更容易在棱角取得交点， 从而导致出现参数为0的情况

回归简单例子

import numpy as np
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

def poly_reg():
    x = np.random.uniform(-3,3,size=100)
    X = x.reshape(-1,1)
    y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)
    plt.scatter(x,y)
    plt.show()
    #线性回归结果及展示
    lin_reg = LinearRegression()
    lin_reg.fit(X,y)
    y_predict = lin_reg.predict(X)
    plt.scatter(x,y)
    plt.plot(x,y_predict,color='r')
    plt.show()
    #多项式回归结果及展示
    x2 = np.hstack([X,X**2])
    lin_reg2 = LinearRegression()
    lin_reg2.fit(x2,y)
    y_predict2 = lin_reg2.predict(x2)
    plt.scatter(x, y)
    x1,y_predict2 = np.sort(x),y_predict2[np.argsort(x)]
    plt.plot(x1,y_predict2,color='r')
    plt.show()
    #使用sklearn的preprocessing进行特征扩展
    poly = PolynomialFeatures(degree=2,include_bias=False)
    poly.fit(X)
    x3 = poly.transform(X)
    lin_reg3 = LinearRegression()
    lin_reg3.fit(x3, y)
    y_predict3 = lin_reg3.predict(x3)
    plt.scatter(x, y)
    x2, y_predict3 = np.sort(x), y_predict3[np.argsort(x)]
    plt.plot(x2, y_predict3, color='r')
    plt.show()
    #输出权重，截距
    print(lin_reg3.coef_,lin_reg3.intercept_)

管道机制

• 管道机制在机器学习算法中得以应用的根源在于，参数集在新数据集（比如测试集）上的重复 使用。
• 管道机制实现了对全部步骤的流式化封装和管理。
• 管道机制不是算法，是一种编程方式
• 管道使用技巧：sklearn.pipeline.Pipeline([(模型名称1，模型1)，(模型名称2，模型2)，。。。])

import numpy as np
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def pipeline_study():
    x = np.random.uniform(-3,3,size=100)
    X = x.reshape(-1,1)
    y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)
    degree = 2
    poly_reg = Pipeline(
        ['poly',PolynomialFeatures(degree=degree)],
        ['std_scaler',StandardScaler()],
        ['lin_reg',LinearRegression()]
    )
    poly_reg.fit(X,y)
    y_predict = poly_reg.predict(X)
    plt.scatter(x,y)
    x1,y_predict2 = np.sort(x),y_predict[np.argsort(x)]
    plt.plot(x1,y_predict2,color='r')
    plt.show()