线性模型-局部加权线性回归 机器学习实战
局部加权线性回归
线性回归的一个问题是有可能出现欠拟合,因为它求的是具有最小均方误差的无偏估计,显然模型欠拟合将无法做出很好的回归预测,所以有些方法允许在估计中引入一些偏差,从而降低预测的均方误差。局部线性加权的思想是对待预测点附近的每个点赋予一个权重,然后在带权的样本上基于最小均方误差来进行回归.
普通线性回归:
局部加权线性回归:
这里唯一的区别是加入了权重θ,采用之前的最小二乘法求解权数w:
![]()
求偏导数:
令导数为0:
![]()
![]()
加权形式
其中加权的θ是一个矩阵,用来给每个数据点赋予权重,LWLR(Locally Weighted Linear Regression)使用‘核’来对数据点赋予权重,核的类型可以自由选择,但一般是与距离成反比的函数,常见的是高斯核:
这样就构造了一个只含对角元素的权重矩阵w,并且点xi与x越接近,θ(i,i)的值越大,当xi与x非常接近时,θ(i,i)的值趋于1,我们再回头看之前的优化式:
对于一个数据点,与其靠近的点,权重大,与其相距较远的点,权重小,从而优化问题会有所偏倚,靠近的点对该数据点的回归拟合起较大作用,而相距较远的点由于权数很小,造成的影响基本可以忽略不计,这样就等同于每个点的回归都是基于与其相距较近的点为基础,而忽略了较远的点,这也就是局部加权线性回归局部的由来,因为它着重考虑目标点局部的数据点为回归基础.
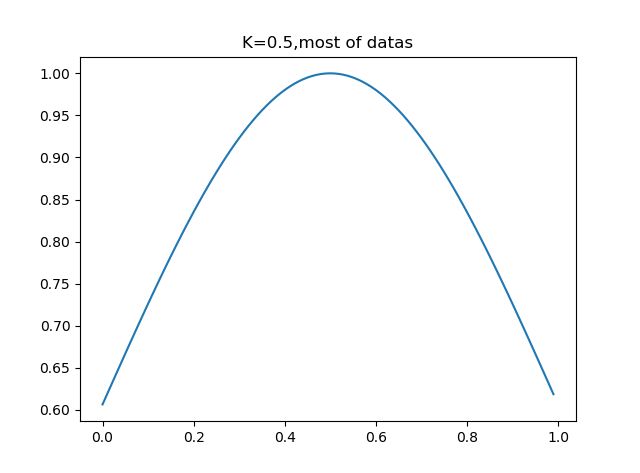
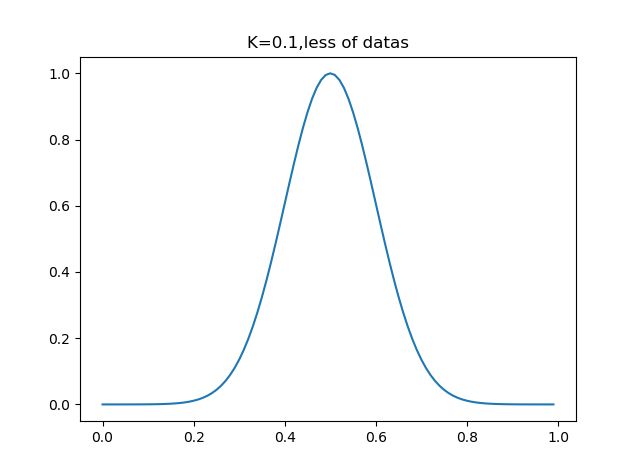
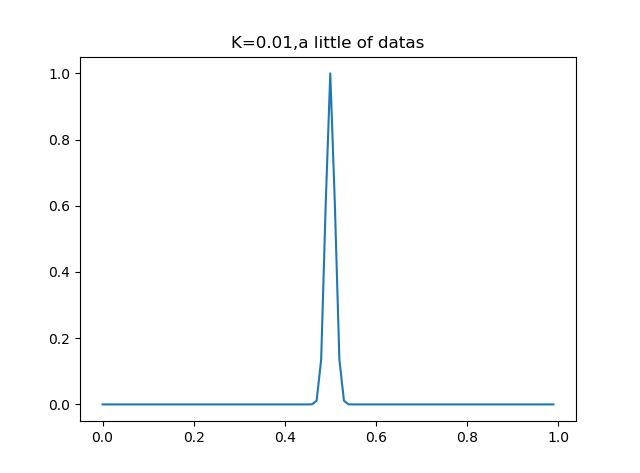
可以看到,加权函数只有一个系数,那就是分母上的K,当K取很小时,exp得到的很多值均趋于0,此时只有很少一部分样本用于训练,而当K取很大时,exp的值不会很快趋于0,从而会有一大部分点用于训练,我们可以通过调整K的值,决定这个‘局部’的大小究竟是多大.
动手看一下K对数据划分的影响:
#画出权数的因素k
def plot_w(k,t_p=0.5):
x = arange(0,1,0.01)
y = exp((x-t_p)**2/(-2*k**2))
plt.plot(x,y)
plt.show()可以看到,k=0.5时,大部分数据用于回归模型,而当k=0.01时,只有非常靠近数据点的数据才会被回归模型所采用.
局部加权回归实现
1)读取数据
from numpy import *
import matplotlib.pyplot as plt
#普通线性回归
#读取数据
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat2)根据加权样本计算权数W
#局部加权线性回归
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = mat(xArr); yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye((m)))#初始化一个单位矩阵
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))#计算数据点周围数据的权数
xTx = xMat.T * (weights * xMat)
if linalg.det(xTx) == 0.0:#判断是否可逆
print ("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * (weights * yMat))#根据公式求出权数W
return testPoint * ws3)得到所有样本的回归预测
#对所有点计算回归值
def lwlrTest(testArr,xArr,yArr,k=1.0): #计算所有数据点的预测回归值,默认k=1,即完全线性回归
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat4)回归可视化
#画出回归方程
def plot_w_figure(xArr,yArr,k=1):
yHat = lwlrTest(xArr,xArr,yArr,k)
xMat = mat(xArr)
srtInd = xMat[:,1].argsort(0)#将输入值x从大到小排序并返回索引
xSort = xMat[srtInd][:,0,:]
# print(xSort.shape)
# print(xSort)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1],yHat[srtInd])#绘制预测点
ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0],s=2,c='red')#绘制初始数据点
plt.show()5)主函数
#主函数
if __name__ == '__main__':
xArr,yArr=loadDataSet('ex0.txt')
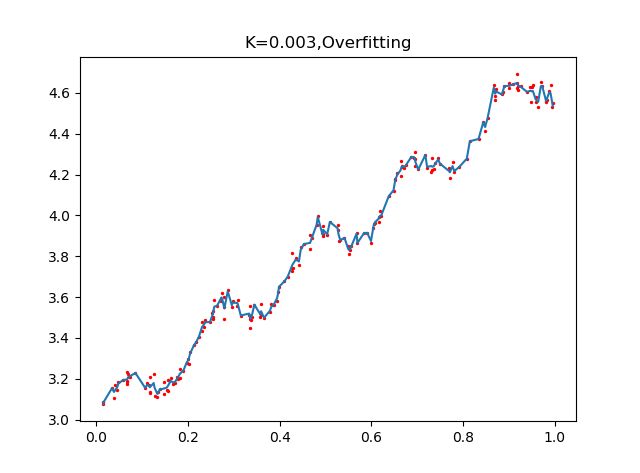
plot_w_figure(xArr,yArr,k=0.01)通过设置不同的k值,看看回归的效果:
可以看到,K=1.0时,加权对样本基本没有影响,结果类似于之前的普通线性回归,k=0.01时,该模型挖掘出数据的潜在规律,而K=0.003时,参数太小导致模型考虑太多的噪声,从而过拟合,虽然对样本数据预测正确率很高,但对于回归预测而言,泛化错误率会非常大.
总结
可以看到,局部加权回归在选择到合适的k时,回归拟合的效果比普通线性回归好很多,但是有一点需要注意,就是局部线性加权回归的计算量很大,因为对于每个数据点,都需要计算与其他数据点的距离矩阵θ,即遍历整个数据集,因此我们还需要探索更加高效简介的算法,减小时间空间开销.