【2019CSP-J 普及组题解】数字游戏(number),公交换乘(transfer),纪念品(souvenir),加工领奖(work) & CSP普及游记
文章目录
- T1:数字游戏
- 题目
- CODE
- T2:公交换乘
- 题目
- CODE
- T3:纪念品
- 题目
- 题解
- CODE
- T4:加工领奖
- 题目
- 题解
- CODE
- 关于普及组的想法&游记
T1:数字游戏
题目
小 K 同学向小 P 同学发送了一个长度为 8 的 01 字符串来玩数字游戏,小 P 同学想 要知道字符串中究竟有多少个 1。
注意:01 字符串为每一个字符是 0 或者 1 的字符串,如“101”(不含双引号)为一 个长度为 3 的 01 字符串。
输入描述:
输入文件只有一行,一个长度为 8 的 01 字符串 s。
输出描述:
输出文件只有一行,包含一个整数,即 01 字符串中字符 1 的个数。
示例1
输入
00010100
输出
2
说明
该 01 字符串中有 2 个字符 1
示例2
输入
11111111
输出
8
说明
该 01 字符串中有 8 个字符 1。
示例3
输入
复制
01010101
输出
复制
4
备注:
对于 20% 的数据,保证输入的字符全部为 0。
对于 100% 的数据,输入只可能包含字符 0 和字符 1,字符串长度固定为 8

CODE
有很多方法,一边输入一边统计,或者存在char/string里面扫一遍即可,C++语言打卡题
#include T2:公交换乘
题目
著名旅游城市 B 市为了鼓励大家采用公共交通方式出行,推出了一种地铁换乘公交 车的优惠方案:
在搭乘一次地铁后可以获得一张优惠票,有效期为 45 分钟,在有效期内可以 消耗这张优惠票,免费搭乘一次票价不超过地铁票价的公交车。在有效期内指 开始乘公交车的时间与开始乘地铁的时间之差小于等于 45 分钟,即: t b u s − t s u b w a y ≤ 45 t_{bus} −t_{subway} ≤ 45 tbus−tsubway≤45
搭乘地铁获得的优惠票可以累积,即可以连续搭乘若干次地铁后再连续使用优惠票搭乘公交车。
搭乘公交车时,如果可以使用优惠票一定会使用优惠票;如果有多张优惠票满 足条件,则优先消耗获得最早的优惠票。
现在你得到了小轩最近的公共交通出行记录,你能帮他算算他的花费吗?
输入描述:
输入文件的第一行包含一个正整数 ,代表乘车记录的数量。
接下来的 行,每行包含 3 个整数,相邻两数之间以一个空格分隔。第 行的 第 1 个整数代表第 条记录乘坐的交通工具,0 代表地铁,1 代表公交车;第 2 个 整数代表第 条记录乘车的票价 p r i c e i price_i pricei;第三个整数代表第 条记录开始乘车的时 间 t i t_i ti(距 0 时刻的分钟数)。
我们保证出行记录是按照开始乘车的时间顺序给出的,且不会有两次乘车记录出现 在同一分钟
输出描述:
输出文件有一行,包含一个正整数,代表小轩出行的总花费
示例1
输入
6
0 10 3
1 5 46
0 12 50
1 3 96
0 5 110
1 6 135
输出
36
说明
第一条记录,在第 3 分钟花费 10 元乘坐地铁。
第二条记录,在第 46 分钟乘坐公交车,可以使用第一条记录中乘坐地铁获得的优 惠票,因此没有花费。
第三条记录,在第 50 分种花费 12 元乘坐地铁。
第四条记录,在第 96 分钟乘坐公交车,由于距离第三条记录中乘坐地铁已超过 45 分钟,所以优惠票已失效,花费 3 元乘坐公交车。
第五条记录,在第 110 分钟花费 5 元乘坐地铁。
第六条记录,在第 135 分钟乘坐公交车,由于此时手中只有第五条记录中乘坐地铁 获得的优惠票有效,而本次公交车的票价为 6 元,高于第五条记录中地铁的票价 5 元, 所以不能使用优惠票,花费 6 元乘坐公交车。
总共花费 36 元。
示例2
输入
6
0 5 1
0 20 16
0 7 23
1 18 31
1 4 38
1 7 68
输出
32
说明
第一条记录,在第 1 分钟花费 5 元乘坐地铁。
第二条记录,在第 16 分钟花费 20 元乘坐地铁。
第三条记录,在第 23 分钟花费 7 元乘坐地铁。
第四条记录,在第 31 分钟乘坐公交车,此时只有第二条记录中乘坐的地铁票价高 于本次公交车票价,所以使用第二条记录中乘坐地铁获得的优惠票。
第五条记录,在第 38 分钟乘坐公交车,此时第一条和第三条记录中乘坐地铁获得 的优惠票都可以使用,使用获得最早的优惠票,即第一条记录中乘坐地铁获得的优惠票。
第六条记录,在第 68 分钟乘坐公交车,使用第三条记录中乘坐地铁获得的优惠票。 总共花费 32 元。
备注:
对于 30% 的数据, n ≤ 1 , 000 , t i ≤ 1 0 6 n≤1,000,t_i\leq 10^6 n≤1,000,ti≤106
另有 15% 的数据, t i ≤ 1 0 7 t_i \leq 10^7 ti≤107, p r i c e i price_i pricei都相等。
另有 15% 的数据, t i ≤ 1 0 9 t_i\leq 10^9 ti≤109, p r i c e i price_i pricei都相等。
对于 100% 的数据, n ≤ 1 0 5 n \leq 10^5 n≤105n, t i ≤ 1 0 9 t_i≤ 10^9 ti≤109, 1 ≤ p r i c e i ≤ 1 , 000 1 ≤ price_i ≤ 1,000 1≤pricei≤1,000
CODE
普及组前面两道题都是C++语言的打卡题,实在不知道如何错(别打我)
这个就是根据题意呗,然后找最前面一个满足要求的优惠票,最暴力的就是输入一个选择,就在之前的选择中去遍历寻找符合要求的答案, O ( n 2 ) O(n^2) O(n2)显然TLE
用一个队列或者手打队列进行维护就是 O ( n ) O(n) O(n)的复杂度了,保证队列里面的优惠卷都是控制在时间差之内的,然后队列的头就是最小的了,作为一个答案选择,弹出。。。

#include T3:纪念品
题目
小伟突然获得一种超能力,他知道未来 T 天 N 种纪念品每天的价格。某个纪念品 的价格是指购买一个该纪念品所需的金币数量,以及卖出一个该纪念品换回的金币数量。
每天,小伟可以进行以下两种交易无限次:
任选一个纪念品,若手上有足够金币,以当日价格购买该纪念品;
卖出持有的任意一个纪念品,以当日价格换回金币。
每天卖出纪念品换回的金币可以立即用于购买纪念品,当日购买的纪念品也可以当日卖出换回金币。当然,一直持有纪念品也是可以的。
T 天之后,小伟的超能力消失。因此他一定会在第 T 天卖出所有纪念品换回金币。
小伟现在有 M 枚金币,他想要在超能力消失后拥有尽可能多的金币。
输入描述:
第一行包含三个正整数 T,N,M,相邻两数之间以一个空格分开,分别代表未来天数 T,纪念品数量 N,小伟现在拥有的金币数量 M。
接下来 T 行,每行包含 N 个正整数,相邻两数之间以一个空格分隔。第 行的 N 个正整数分别为 P i , 1 P_{i,1} Pi,1, P i , 2 P_{i,2} Pi,2, … … … … , P i , n \dots\dots…… ,P_{i,n} …………,Pi,n
表示第 天第 种纪念品的价格
输出描述:
输出仅一行,包含一个正整数,表示小伟在超能力消失后最多能拥有的金币数量
示例1
输入
6 1 100
50
20
25
20
25
50
输出
305
说明
最佳策略是:
第二天花光所有 100 枚金币买入 5 个纪念品 1;
第三天卖出 5 个纪念品 1,获得金币 125 枚;
第四天买入 6 个纪念品 1,剩余 5 枚金币;
第六天必须卖出所有纪念品换回 300 枚金币,第四天剩余 5 枚金币,共 305 枚金币。
超能力消失后,小伟最多拥有 305 枚金币
示例2
输入
3 3 100
10 20 15
15 17 13
15 25 16
输出
217
说明
最佳策略是:
第一天花光所有金币买入 10 个纪念品 1;
第二天卖出全部纪念品 1 得到 150 枚金币并买入 8 个纪念品 2 和 1 个纪念品 3,剩 余 1 枚金币;
第三天必须卖出所有纪念品换回216 枚金币,第二天剩余1枚金币,共 217 枚金币。
超能力消失后,小伟最多拥有 217 枚金币
备注:
对于 10% 的数据, T = 1 T=1 T=1。
对于 30% 的数据, T ≤ 4 , N ≤ 4 , M ≤ 100 T≤4,N≤4,M≤100 T≤4,N≤4,M≤100,所有价格 10 ≤ P i , j ≤ 100 10≤P_{i,j}≤100 10≤Pi,j≤100。
另有 15% 的数据, T ≤ 100 , N = 1 T≤100,N=1 T≤100,N=1。
另有 15% 的数据, T = 2 , N ≤ 100 T=2,N≤100 T=2,N≤100。
对于 100% 的数据, T ≤ 100 , N ≤ 100 , M ≤ 1 0 3 T≤100,N≤100,M≤10^3 T≤100,N≤100,M≤103,所有价格 1 ≤ P i , j ≤ 1 0 4 1 ≤ P_{i,j} ≤ 10^4 1≤Pi,j≤104,数据保证任意时刻,小明手上的金币数不可能超过 1 0 4 10^4 104
题解
首先对于10pots,直接输出m,让你不至于报零,真良心
我们直接进入正解:

首先的贪心思想大家都能想到的就是:如果第i天的第j种商品在i天买进,第i+1天卖出去能产生收益,即 p [ i + 1 ] [ j ] − p [ i ] [ j ] > 0 p[i+1][j]-p[i][j]>0 p[i+1][j]−p[i][j]>0,就应该购入并在下一天卖出,这样产生的收益一定是最大的
因此问题演变为今天买入哪些商品能在下一天获取最大利益
再分析一下:今天的钱数m,商品价格 p [ i ] [ j ] p[i][j] p[i][j],商品利益 p [ i + 1 ] [ j ] − p [ i ] [ j ] p[i+1][j]-p[i][j] p[i+1][j]−p[i][j],
如何用m钱买入若干种商品获取最大利益,显然是背包问题
又因为数据保证任意时刻,小明手上的金币数不可能超过 1 0 4 10^4 104,可以笃定背包不会超时
故在每一天都重新用一次背包转移出用手上所拥有的钱数能产生多少利益
设 d p [ k ] dp[k] dp[k]表示用 k k k枚金币能产生的最大利益,则 d p [ m ] dp[m] dp[m]就是当天所赚的利益
转移方程式如下,如果不能理解的欢迎评论或者自行学习背包
d p [ k ] = m a x ( d p [ k ] , d p [ k − p [ i ] [ j ] ] + p [ i + 1 ] [ j ] − p [ i ] [ j ] ) dp[k]=max(dp[k],dp[k-p[i][j]]+p[i+1][j]-p[i][j]) dp[k]=max(dp[k],dp[k−p[i][j]]+p[i+1][j]−p[i][j])

CODE
#include T4:加工领奖
题目
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 n 位工人,工人们从 1 ∼ n 1 \sim n 1∼n 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 x 号工人想生产一个被加工到第 L ( L > 1 ) (L \gt 1) (L>1)阶段的零件,则所有与 x 号工人有传送带直接相连的工人,都需要生产一个被加工到第 L - 1 阶段的零件(但 x 号工人自己无需生产第 L - 1 阶段的零件)。
如果 x 号工人想生产一个被加工到第 1 阶段的零件,则所有与 x 号工人有传送带直接相连的工人,都需要为 x 号工人提供一个原材料。
轩轩是 1 号工人。现在给出 q 张工单,第 i 张工单表示编号为 a i a_i ai的工人想生产一个第 L i L_i Li阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
输入格式
第一行三个正整数 n,m 和 q,分别表示工人的数目、传送带的数目和工单的数目。
接下来 m 行,每行两个正整数 u 和 v,表示编号为 u 和 v 的工人之间存在一条零件传输带。保证 u ≠ v u \neq v u=v
接下来 q 行,每行两个正整数 a 和 L,表示编号为 a 的工人想生产一个第 L 阶段的零件。
输出格式
共 q 行,每行一个字符串 Yes 或者 No。如果按照第 i 张工单生产,需要编号为 1 的轩轩提供原材料,则在第 i 行输出 Yes;否则在第 i 行输出 No。注意输出不含引号。
输入输出样例
输入
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2
输出
No
Yes
No
Yes
No
Yes
输入
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5
输出
No
Yes
No
Yes
Yes
说明/提示
【输入输出样例 1 说明】

编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
【输入输出样例 2 说明】
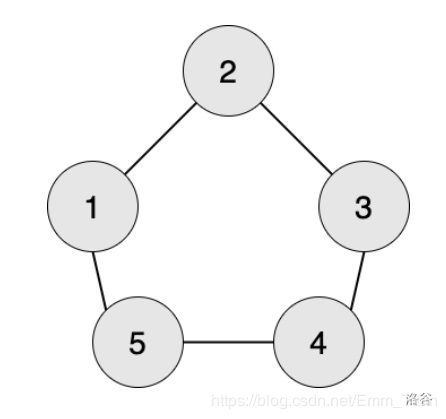
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为 1,3,4 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为 1,3,4 的工人生产第 1 阶段的零件,需要编号为 2,3,4,5 的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为 1,3,4 的工人生产第 2 阶段的零件,需要编号为 2,3,4,5 的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为 1,3,4 的工人生产第 3 阶段的零件,需要编号为 2,3,4,5 的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料。
【数据规模与约定】
共 20 个测试点。
1 ≤ u , v , a ≤ n 1 \leq u, v, a \leq n 1≤u,v,a≤n
测试点 1~4, 1 ≤ n , m ≤ 1000 1 \leq n, m \leq 1000 1≤n,m≤1000, q = 3 q=3 q=3, L = 1 L = 1 L=1
测试点 5~8, 1 ≤ n , m ≤ 1000 1 \leq n, m \leq 1000 1≤n,m≤1000, q = 3 q = 3 q=3, 1 ≤ L ≤ 10 1 \leq L \leq 10 1≤L≤10
测试点 9~12, 1 ≤ n , m , L ≤ 1000 1 \leq n, m, L \leq 1000 1≤n,m,L≤1000, 1 ≤ q ≤ 100 1 \leq q \leq 100 1≤q≤100
测试点 13~16, 1 ≤ n , m , L ≤ 1000 1 \leq n, m, L \leq 1000 1≤n,m,L≤1000, 1 ≤ q ≤ 1 0 5 1 \leq q \leq 10^5 1≤q≤105
测试点 17~20, 1 ≤ n , m , q ≤ 1 0 5 1 \leq n, m, q \leq 10^5 1≤n,m,q≤105 , 1 ≤ L ≤ 1 0 9 1 \leq L \leq 10^9 1≤L≤109
题解
首先我们要提取出题目描述中所隐含的想法,举个栗子:假设1,2号工人之间有生产线,那么如果1号想生产第3阶段的零件,那么2号工人就要生产第2阶段零件,此时的1号工人必须生产第1阶段零件,原材料则由2号工人提供,所以这个过程就是两点之间不停的来回跑,
在此基础上,我们提出了一个想法如果v号工人距离1号工人的距离为 x x x,那么要生产 L L L阶段的零件,1号工人就要生产 L − x , L − x − 2 , L − x − 4... L-x,L-x-2,L-x-4... L−x,L−x−2,L−x−4...阶段的零件,而与1号工人相邻的生产线就要生产 L − x + 1 , L − x − 1 , L − x − 3... L-x+1,L-x-1,L-x-3... L−x+1,L−x−1,L−x−3...阶段的零件,当工人需要生产0阶段的零件时意味着他就是需要提供原材料的
于是发现我们只需要判断是否出现 L − x − y = 0 ( y L-x-y=0(y L−x−y=0(y% 2 = = 0 ) 2==0) 2==0)的情况即可,存在为零的情况吗?

只需要满足 L L L与 x x x必须同奇同偶,才可能有出现为0的情况
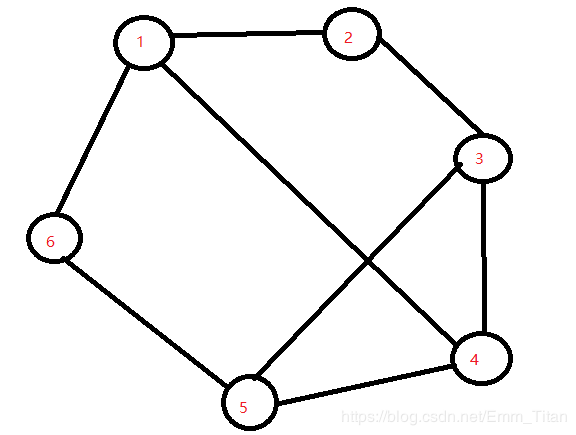
但是图可能是有环的,所以对于一个工人而言,他与1号工人的距离是可能有奇数距离也可能有偶数的距离,而且距离可能存在多条,为了在要求生产零件的阶段一样时,能让该号工人尽可能波及到1号工人,让1号工人有产生原材料的可能,(如果距离不够,1号工人与该工人要生产的零件一点关系都扯不上, 这也解释了上面加粗的可能二字)
所以我们要去寻找到最小奇距离,最小偶距离,简单的一个bfs就可以搜出来
具体的代码解释在CODE里面
CODE
#include 好了,讲解完毕,接下来不愿看的可以跳过了
接下来就是bb普及组的问题以及常规套路
关于普及组的想法&游记
对于第1题,近两年都是输入一行字符串,进行一个简单的 i f − e l s e if-else if−else判断,数字的个数?小写字母的个数?大写字母的个数…所以我猜下一次多半也是这样,毕竟打卡题只能这么考了
对于第2题,也是在一个大的 f o r for for循环下面进行一些简单的判断操作,去年的龙虎斗,今年的公交换乘,都会把时间控制在 O ( n l o g n ) O(nlogn) O(nlogn)之内,并且不涉及高端操作或者高级算法,毕竟是个普及 ,唯独可能会卡一卡 l o n g long long l o n g long long,分析好就可以了
对于第3题,亘古不变都是 d p dp dp,而且是背包问题的变式,因为 d p dp dp对于以后学习的高级算法是很有关系的,所以出题人会考察学生是否掌握 d p dp dp,今年的纪念品比去年的摆渡车要简单很多,但是 d p dp dp是很考验人的思维的,如何转化极其重要,反正我最差的就是dp
对于第4题,既不能上升到提高组的难度,又不能比前面的简单,那能考的就剩下简单的数据结构或者图论,最短路?最小生成树?lca?线段树?…但是如果考的是比较模板的题目,就会把它隐藏起来,需要我们去挖掘出来,今年的加工领奖亦是如此,只要挖掘出了是最小奇距离和最小偶距离,简单的最短路甚至都不需要,一个bfs就搞定了。。。我明明考场上就是这么想的,也是这么打的,但是没去推同奇同偶,所以答案输出处理出错,就GG了,幸好打了前面的暴力分,保住了一点小命
让我们剑指2020CSP普及,不见不散