哈希表的实现（闭散列法和拉链法）

哈希表

哈希表(Hash Table)也叫散列表，是根据关键码值（Key Value）而直接进行访问的数据结构。它通过把关键码值映射到哈希表中的一个位置来访问记录，以加快查找的速度。这个映射函数就做散列函数，存放记录的数组叫做散列表。

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。
如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素。

例如：数据集合{180，750，600，430，541，900，460

用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快

哈希冲突

按照上述哈希方式，向集合中插入元素43，会出现什么问题？

&nbps; 对于两个数据元素的关键字 i 和 j （i != j），有 i！= j ，但有： HashFun(i) == HashFun(j)
即不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。

哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。

哈希函数设计原则：
    - 哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值域
必须在0到m-1之间
    - 哈希函数计算出来的地址能均匀分布在整个空间中
    - 哈希函数应该比较简单  

【常见哈希函数】

1)直接定址法

**取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B**  
优点：简单、均匀  
缺点：需要事先知道关键字的分布情况,适合查找比较小且连续的情况  
面试题：找出一个字符串中第一个只出现一次的字符，要求：时间复杂度O(N)，空间复杂度O(1)  

2）除留余数法

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：
Hash(key) = key% p(p<=m),将关键码转换成哈希地址 

3）平方取中法

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；  
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址  
**平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况** 

4）折叠法

折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这几部分叠加
求和，并按散列表表长，取后几位作为散列地址  折叠法适合事先不需要知道关键字的分布，适合关键
字位数比较多的情况

5）随机数法

选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中random
为随机数函数  
通常应用于关键字长度不等时采用此法

处理哈希冲突

---

解决哈希冲突两种常见的方法是：闭散列和开散列

闭散列

闭散列：也叫开放地址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到表中“下一个” 空位中去 。
那如何寻找下一个空位？

1.线性探测

设关键码集合为{37, 25, 14, 36, 49, 68, 57, 11}，散列表为HT[12]，表的大小m = 12，假设哈希函数为：
Hash(x) = x %p（p = 11，是最接近m的质数），就有： 
Hash(37) = 4  
Hash(25) = 3  
Hash(14) = 3  
Hash(36) = 3  
Hash(49) = 5  
Hash(68) = 2  
Hash(57) = 2  
Hash(11) = 0  
其中25，14，36以及68，57发生哈希冲突，一旦冲突必须要找出下一个空余位置  
线性探测找的处理为：从发生冲突的位置开始，依次继续向后探测，直到找到空位置为止 
【插入】  
1. 使用哈希函数找到待插入元素在哈希表中的位置  
2. 如果该位置中没有元素则直接插入新元素；如果该位置中有元素且和待插入元素相同，则不用插入；如果
该位置中有元素但不是待插入元素则发生哈希冲突，使用线性探测找到下一个空位置，插入新元素；

下面是闭散列哈希表的实现参考代码：

哈希表的数据结构：

typedef int KeyType;
typedef int ValueType;

typedef enum Status
{
    EMPTY,
    EXITS,
    DELETED,
}Status;

typedef struct HashNode
{
    KeyType _key;
    ValueType _value;
    Status _status;
}HashNode;

#pragma once

#include 
#include 

typedef int KeyType;
typedef int ValueType;

typedef enum Status
{
    EMPTY,
    EXITS,
    DELETED,
}Status;

typedef struct HashNode
{
    KeyType _key;
    ValueType _value;
    Status _status;
}HashNode;

typedef struct HashTable
{
    HashNode* _tables;
    size_t _size;
    size_t _N;
}HashTable;

void HashTableInit(HashTable* ht);
int HashTableInsert(HashTable* ht, KeyType key, ValueType value);
HashNode* HashTableFind(HashTable* ht, KeyType key);
int HashTableRemove(HashTable* ht, KeyType key);
int HashTableDestory(HashTable* ht);



size_t GetNextPrimeSize(size_t num)
{
    // 使用素数表对齐做哈希表的容量，降低哈希冲突
    const int PrimeSize = 28;
    static const unsigned long PrimeList[] =
    {
        53ul, 97ul, 193ul, 389ul, 769ul,
        1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
        49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
        1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
        50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
        1610612741ul, 3221225473ul, 4294967291ul
    };
    for (size_t i = 0; i < PrimeSize; i++)
    {
        if (num * 10 / PrimeList[i] <= 7)
            return PrimeList[i];
    }
    return PrimeList[PrimeSize - 1];        //最大返回容量约4G
}

//初始化哈希表
void HashTableInit(HashTable* ht,size_t N)
{
    assert(ht);

    ht->_size = 0;
    ht->_N = N;
    ht->_tables = (HashNode* )malloc(ht->_N * sizeof(HashNode));
    assert(ht->_tables);
    for (int i = 0; i < ht->_N; i++)
    {
        ht->_tables[i]._status = EMPTY;
    }
}

size_t HashFunc(KeyType key,size_t N)
{
    return key % N;
}

//插入
int HashTableInsert(HashTable* ht,KeyType key,ValueType value)
{
    assert(ht);
    if (ht->_size*10 / ht->_N > 7)      //增容
    {
        HashTable NewTables;
        HashTableInit(&NewTables,GetNextPrimeSize(ht->_size));

        for (size_t i = 0; i < ht->_N; i++)
        {
            if (ht->_tables[i]._status == EXITS)
                HashTableInsert(&NewTables, ht->_tables[i]._key, 0);
            else
                NewTables._tables[i]._status = ht->_tables[i]._status;
        }   
        free(ht->_tables);
        ht->_tables = NewTables._tables;
        ht->_N = NewTables._N;

    }

    size_t index = HashFunc(key,ht->_N);
    while ((ht->_tables[index])._status == EXITS)
    {
        if (index == ht->_N)
        {
            index = 0;
            continue;
        }
        index++;
    }
    ht->_tables[index]._key = key;
    ht->_tables[index]._value = value;
    ht->_tables[index]._status = EXITS;
    ht->_size++;
    return 1;
}

//打印哈希表
void HashTablePrint(HashTable* ht)
{
    for (size_t i = 0; i < ht->_N; i++)
    {
        if (ht->_tables[i]._status == EXITS)
            printf("[%d]:%d  ",i,ht->_tables[i]._key);
        else if (ht->_tables[i]._status == DELETED)
            printf("[%d]:D  ", i);
        else
            printf("[%d]:E  ", i);
    }
}
//查找，成功返回结点地址，失败返回NULL
HashNode* HashTableFind(HashTable* ht, KeyType key)
{
    assert(ht);
    size_t index = HashFunc(key,ht->_N);
    while (ht->_tables[index]._status == EXITS)
    {
        if (ht->_tables[index]._key == key)
            return &(ht->_tables[index]);
        index++;
    }
    return NULL;
}

//删除，成功返回1，失败返回0
int HashTableRemove(HashTable* ht, KeyType key)
{

    HashNode* tmp = HashTableFind(ht,key);
    if (tmp == NULL)
        return 0;
    else
    {
        tmp->_status = DELETED;
        return 1;
    }   
}

int HashTableDestory(HashTable* ht)
{
    free(ht->_tables);
    ht->_tables = NULL;
    ht->_size = 0;
    ht->_N = 0;
    return 0;
}

void TestHashTable()
{
    HashTable ht;
    HashTableInit(&ht, GetNextPrimeSize(0));
    //HashTableInsert(&ht, 53, 0);
    //HashTableInsert(&ht, 106, 0);
    ////HashTableInsert(&ht, 54, 0);
    //HashTableInsert(&ht, 55, 0);
    //HashTableInsert(&ht, 59, 0);
    //HashTableInsert(&ht, 66, 0);

    for (size_t i = 0; i < 440; i++)
        HashTableInsert(&ht, i, 0);

    HashTableInsert(&ht, 43, 0);

    HashTablePrint(&ht);
    if (HashTableFind(&ht, 54) != NULL)
        printf("在哈希表中找到了54\n");
    else
        printf("在哈希表中没找到54\n");

}

开散列

开散列法又叫链地址法(开链法)。
开散列法：首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

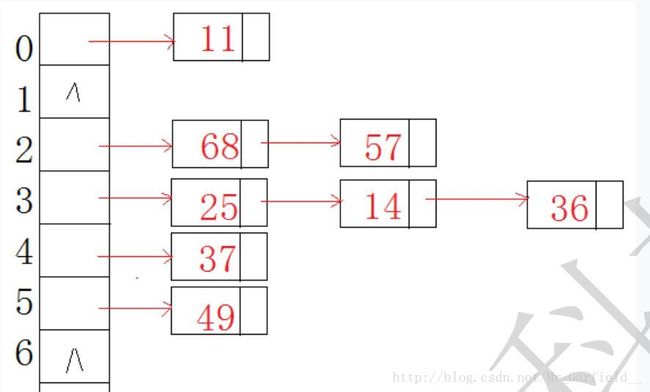
    设元素的关键码为37, 25, 14, 36, 49, 68, 57, 11, 散列表为HT[12]，表的大小为12，散列函数为
    Hash(x) = x % 11  
        Hash(37)=4  
        Hash(25)=3  
        Hash(14)=3  
        Hash(36)=3  
        Hash(49)=5  
        Hash(68)=2  
        Hash(57)=2  
        Hash(11)=0  

使用哈希函数计算出每个元素所在的桶号，同一个桶的链表中存放哈希冲突的元素。

哈希表拉链法参考代码：

#pragma once

typedef int KeyType;
typedef int ValueType;

#include 
#include 
#include 
#include 

typedef struct HashNode
{
    KeyType _key;
    ValueType _value;

    struct HashNode* _next;
}HashNode;

typedef struct HashTable
{
    HashNode** _tables;
    size_t _size;
    size_t _N;
}HashTable;

HashNode* BuyHashNode(KeyType key, ValueType value);
void HashTableInit(HashTable* ht, size_t N);
int HashTableInsert(HashTable* ht, KeyType key, ValueType value);
HashNode* HashTableFind(HashTable* ht, KeyType key);
int HashTableRemove(HashTable* ht, KeyType key);
int HashTableDestroy(HashTable* ht);

HashNode* BuyHashNode(KeyType key, ValueType value)
{
    HashNode* ht = (HashNode*)malloc(sizeof(HashNode));
    ht->_key = key;
    ht->_value = value;
    ht->_next = NULL;
    return ht;
}

size_t GetNextPrimeSize(size_t num)
{
    // 使用素数表对齐做哈希表的容量，降低哈希冲突
    const int PrimeSize = 28;
    static const unsigned long PrimeList[] =
    {
        53ul, 97ul, 193ul, 389ul, 769ul,
        1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
        49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
        1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
        50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
        1610612741ul, 3221225473ul, 4294967291ul
    };
    for (size_t i = 0; i < PrimeSize; i++)
    {
        if (num * 10 / PrimeList[i] <= 7)
            return PrimeList[i];
    }
    return PrimeList[PrimeSize - 1];        //最大返回容量约4G
}

void HashTableInit(HashTable* ht, size_t N)
{
    assert(ht);
    ht->_size = 0;
    ht->_N = N;
    ht->_tables = (HashNode** )malloc(ht->_N*sizeof(HashNode *));
    assert(ht->_tables);
    memset(ht->_tables, NULL, ht->_N*sizeof(HashNode *));
}

size_t HashFunc(KeyType key,size_t N)
{
    return key % N;
}

int HashTableInsert(HashTable* ht, KeyType key, ValueType value)
{
    assert(ht);
    //if (ht->_size == ht->_N)//扩容
    //{
    //}
    size_t index = HashFunc(key, ht->_N);

    HashNode *node = BuyHashNode(key, value);
    node->_next = ht->_tables[index];
    ht->_tables[index] = node;
    ht->_size++;
    return 0;
}

HashNode* HashTableFind(HashTable* ht, KeyType key)
{
    assert(ht);
    size_t index = HashFunc(key, ht->_N);
    HashNode* cur = ht->_tables[index];
    while (cur)
    {
        if (cur->_key == key)
            return cur;
        cur = cur->_next;
    }
    return NULL;
}

int HashTableRemove(HashTable* ht,KeyType key)
{
    assert(ht);
    HashNode* cur = HashTableFind(ht,key);
    if (cur == NULL)
        return 0;
    else
    {
        size_t index = HashFunc(key, ht->_N);
        if (key == ht->_tables[index])
        {
            ht->_tables[index] = ht->_tables[index]->_next;
            free(cur);
        }
        else
        {
            ht->_tables[index]->_next = cur->_next;
            free(cur);
        }

    }
}

void HashTablePrint(HashTable* ht)
{
    assert(ht);
    for (size_t i = 0; i < ht->_N; i++)
    {
        printf("[%d]->", i);
        HashNode* cur = ht->_tables[i];
        while (cur)
        {
            printf("%d->",cur->_key);
            cur = cur->_next;
        }
        printf("NULL\n");
    }
}

void TestHashTable()
{
    HashTable ht;
    HashTableInit(&ht, GetNextPrimeSize(0));
    for (size_t i = 0; i < 88; i++)
    {
        HashTableInsert(&ht,i,0); 
    }
    HashTableInsert(&ht,22,0);
    HashTablePrint(&ht);

    if (HashTableFind(&ht,88) != NULL)
        printf("88在哈希表中");
    else
        printf("88不在哈希表中");
}