Redis面试题系列:跳跃表
简介
跳跃表(skiplist)是一种有序数据结构,它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。在大部分情况下,跳跃表的效率可以和平衡树相媲美,而且实现比平衡树更加简单。
Redis 使用跳跃表作为有序集合的底层实现之一,如果一个有序集合包含的元素较多,或者有序集合中的元素是较长的字符串时,Redis 就会使用跳跃表来维护数据。
接下来一起看下跳跃表的原理和基于C++的实现代码。

基本原理
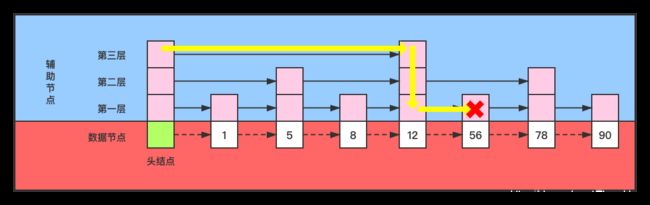
跳跃表本质上是个有序的链表,其通过在节点上随机的添加辅助连接使得查找的时间复杂度从O(N)变为平均O(logN),最坏O(N)。

如上图所示,每个节点都有添加了辅助连接。我们可以通过辅助节点来加快搜索过程:在顶层的链表进行扫描,直到 遇到一个含有较小关键字且指向一个含有较大关键字节点的节点,或者到达这一层的最后一个节点,然后下降到下一层辅助节点继续查找,直到确认目标值不存在或者找到了目标值所在节点。举个例子,在上图中跳跃表寻找 58 的过程如下:
- 初始时,位于头指针的第三层辅助节点。
- 通过当前辅助节点的next指针发现下一个节点的值为 12。
因为12比目标值小,所以直接移动到 12 的第三层辅助节点。 - 因为 12 是最后一个第三层辅助节点,所以下降到第二层。
- 通过当前节点的next指针发现下一个节点为 78。
因为 78 比目标值大,所以继续下降到第一层辅助节点。 - 通过当前节点的next指针发现下一个节点为 56。
因为 56 比目标值小,所以向后移动到 56 的第一层辅助节点。 - 因为当前节点的数据比目标值小,且下一个节点的值(78)比目标值大,且此时已位于最低一层辅助节点,所以判定目标值不存在于该跳跃表中。查找结束。
Q:查找过程中为何没有用到数据节点自身的next指针呢?
A: 因为第一层的辅助节点等价于数据节点自身的next。其实在跳跃表中,数据节点只有数据,辅助节点中只有next指针。
Q: 当数据节点变多时,三层辅助节点好像不太够用?
A: 当跳跃表的数据节点变多时,我们可以加入更多层的辅助节点来保证足够快的查找速度。
跳跃表的初始化
为了初始化跳跃表,我们需要一个头结点,它含有M层辅助节点,每个辅助节点都指向NULL。M是整个跳跃表中辅助节点的层数上限。SkipList 类的定义如下,我们在构造函数中对头结点进行初始化。
// SkipList 的定义
template<typename DataType>
class SkipList {
enum {
MAX_LEVEL = 32, // 允许的最大层数
};
struct Node {
std::vector<Node*> next; //存储辅助信息的 next
DataType data; // 数据
};
private:
uint8_t max_level; //真正指定的最大层数
Node head_node; //头结点
int randomLevelNumber() const; //以概率 1/2^j 返回 j, j ∈ [1, max_level];
public:
SkipList(uint8_t ml = MAX_LEVEL) : max_level(ml) {
if(max_level > MAX_LEVEL || max_level <= 2) {
max_level = MAX_LEVEL;
}
head_node.next.resize(max_level); // 初始化头结点的 next 数组,全部指向 nullptr;
}
bool isExist(const DataType &) const; // 判断目标元素是否存在
bool erase(const DataType &); // 删除元素
bool insert(const DataType &); // 插入元素
typedef function<bool(const DataType&)> HandlerType;
void walk(HandlerType &) const; // 暴露一个遍历接口
};
插入
当我们向跳跃表插入一个新节点时,需要解决的第一个问题就是新增节点要有多少层next指针。如果每 t 个节点中就有一个节点至少具备两层 next 指针,则我们在第二层可以一次跳跃 t 个节点,以此类推,每 t^j 个节点中,就有一个节点至少具备j+1层next指针。
为使节点具有上述性质,我们需要一个以概率 1/t^j 返回 j+1 的 随机函数。
// 随机函数的定义
// FIXME
// 这里有点问题,i 为 max_level 和 max_level-1 的概率是相同的,
template<typename DataType>
int SkipList<DataType>::randomLevelNumber() const {
int i, j, t = rand();
for(i = 1, j = 2; i < max_level; i++, j *= 2) {
if(t > RAND_MAX/j) {
break;
}
}
return i;
}
// 插入函数
template<typename DataType>
bool SkipList<DataType>::insert(const DataType &data) {
if(isExist(data)) {
return false;
}
int level = randomLevelNumber();
Node *new_node = new Node();
new_node->data = data;
new_node->next.resize(level);
int cur_level = max_level - 1; // 因为 level 是从 0 开始的。
Node *cur_node = &head_node;
while(cur_level >= 0) {
while(cur_node->next[cur_level] != nullptr
&& cur_node->next[cur_level]->data < data) {
cur_node = cur_node->next[cur_level];
}
if(new_node->next.size() > cur_level) {
new_node->next[cur_level] = cur_node->next[cur_level];
cur_node->next[cur_level] = new_node;
}
-- cur_level;
}
return true;
}
调用了 1666112 次,得到的层数基本还是符合预期的,具体的分布如下:
| 层数 | 数量 | 比率 |
|---|---|---|
| 23 | 1 | 6.002e-07 |
| 22 | 1 | 6.002e-07 |
| 20 | 1 | 6.002e-07 |
| 19 | 3 | 1.8006e-06 |
| 18 | 7 | 4.2014e-06 |
| 17 | 15 | 9.003e-06 |
| 16 | 38 | 2.28076e-05 |
| 15 | 66 | 3.96132e-05 |
| 14 | 105 | 6.3021e-05 |
| 13 | 214 | 0.000128443 |
| 12 | 367 | 0.000220273 |
| 11 | 813 | 0.000487962 |
| 10 | 1598 | 0.000959119 |
| 9 | 3265 | 0.00195965 |
| 8 | 6385 | 0.00383228 |
| 7 | 13078 | 0.00784941 |
| 6 | 25849 | 0.0155146 |
| 5 | 52201 | 0.031331 |
| 4 | 103711 | 0.0622473 |
| 3 | 207830 | 0.12474 |
| 2 | 417042 | 0.250309 |
| 1 | 833522 | 0.50028 |
这个随机函数保证:
- 平均每 1 个节点中就有一个至少具备 1 层辅助连接的节点。
- 平均每 2 个节点中就有一个至少具备 2 层辅助连接的节点。
- 平均每 4 个节点中就有一个至少具备 3 层辅助连接的节点。
- 平均每 8 个节点中就有一个至少具备 4 层辅助连接的节点。
- 以此类推。。。
- 平均每 2^i 个节点中就有个一个至少具备 i-1 层辅助连接的节点。
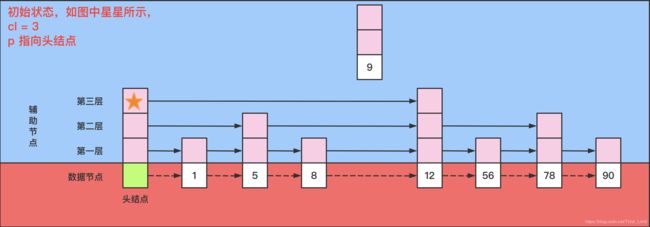
插入的步骤
插入的步骤和搜索的套路类似,只是需要在插入过程中更新对应层的 next 指针,具体的流程如下:
- 首先判断待插入数据 x 是否已经存在于跳表中,如果存在则插入失败。
- 其次和链表的插入类似,需要先 new 一个结点 q 用于存储数据。
- 插入开始前,设指针 p 位于头结点的最高层,设当前层数为 cl。
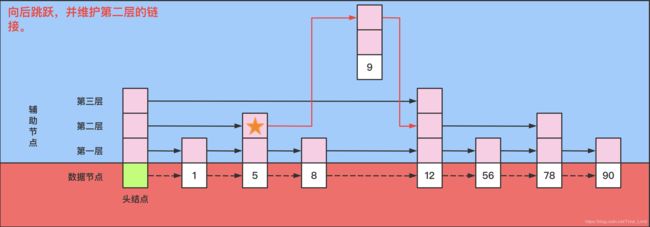
- 移动 p,直到 p->next[cl] 为空或者 p->data 小于 p->next[cl]->data。
- 如果q在当前有指针,那么更新指针:
- q->next[cl] = p->next[cl]->next[cl]
- p->next[cl] = q
- 如果此时已位于最后一层,则插入结束。否则下降一层,即 cl -= 1,然后跳转步骤 4。
删除
删除和插入过程类似,只是从建立链接变成了删除链接,寻找目标节点的流程是一样的,就不再赘述了。
template<typename DataType>
bool SkipList<DataType>::erase(const DataType &data) {
int cur_level = max_level - 1;
Node *cur_node = &head_node;
while(cur_level >= 0) {
while(cur_node->next[cur_level] != nullptr
&& cur_node->next[cur_level]->data < data) {
cur_node = cur_node->next[cur_level];
}
if(cur_node->next[cur_level] != nullptr
&& !(data < cur_node->next[cur_level]->data)) {
auto remove_node = cur_node->next[cur_level];
cur_node->next[cur_level] = cur_node->next[cur_level]->next[cur_level];
remove_node->next[cur_level] = nullptr;
if(cur_level == 0) {
delete(remove_node);
}
}
--cur_level;
}
return 0;
}
总结
- 相比单向链表,查找的时间复杂度从O(n) 降为 O(logN)。
- 相比数组,删除插入的时间复杂度从O(n) 降为 O(logN),且无需扩容/缩容操作。
- 相比平衡树/红黑树,各种操作的效率差不多,但是跳表不稳定。而且跳表的空间开销相比于后者有所增加。
- 另外,可存储重复键值的跳表该如何实现呢?每个节点变为链表以解决冲突?
全部代码
#include