AVL树(一种二叉平衡搜索树)

普通的二叉搜索树,深度不一定为为O(logn),那么则是不平衡的

如果不进行删除操作或进行极少的删除操作(可利用懒惰删除),提出一种解决方案,即AVL Tree,任意节点左右子树的高度差绝对值不超过1,规定空树的高度为-1,即一个单独节点的高度为0

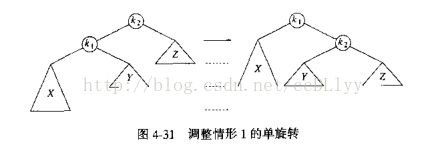
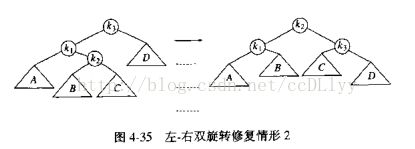
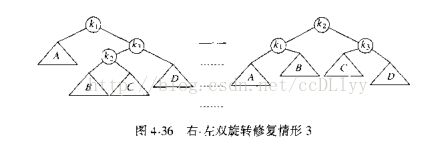
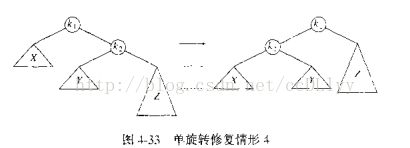
当进行插入操作,插入过程同二叉搜索树,插入后,插入路径上节点的平衡可能遭到破坏,从插入点到根结点的路径上(即自下而上)找到第一个失去平衡的节点,调平衡,由调平衡的过程和图分析可以证明,该点调完平衡,该路径上的点已经平衡,即AVL树已经恢复平衡

调平衡的方式为旋转,分为单旋(LL和RR)双旋(LR和RL)

代码：

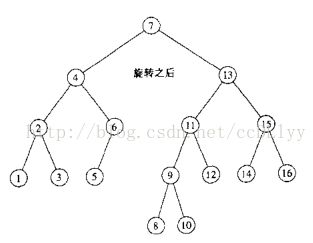
以往空树中依次插入3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9为例

插入结束后,得到：

中序遍历的结果：

基于指针实现（未封装）

#include 
#include 
#include 
#include 
using namespace std;
struct node{
	int data;
	struct node* left;
	struct node* right;
	int height;
};
void InOrderTrversal(struct node* tree){
	if(tree==NULL)
		return;
	InOrderTrversal(tree->left);
	printf(" %d",tree->data);
	InOrderTrversal(tree->right);
}
int GetHeight(struct node* tree){
	if(tree==NULL)
		return -1;
	else
		return tree->height;
}
struct node* SingleRotateWithLeft(struct node* k1){
	struct node* k2=k1->left;
	k1->left=k2->right;
	k2->right=k1;
	k1->height=max(GetHeight(k1->left),GetHeight(k1->right))+1;
	k2->height=max(GetHeight(k2->left),GetHeight(k2->right))+1;
	return k2;
}
struct node* SingleRotateWithRight(struct node* k1){
	struct node* k2=k1->right;
	k1->right=k2->left;
	k2->left=k1;
	k1->height=max(GetHeight(k1->left),GetHeight(k1->right))+1;
	k2->height=max(GetHeight(k2->left),GetHeight(k2->right))+1;
	return k2;
}
struct node* DoubleRotateWithLeft(struct node* k1){//LR双旋相当于左儿子先RR单旋,自己再LL单旋
	k1->left=SingleRotateWithRight(k1->left);
	k1=SingleRotateWithLeft(k1);
	return k1;
}
struct node* DoubleRotateWithRight(struct node* k1){//RL双旋相当于右儿子先LL单旋,自己再RR单旋
	k1->right=SingleRotateWithLeft(k1->left);
	k1=SingleRotateWithRight(k1);
	return k1;
}
struct node* Insert(struct node* tree,int x){
	if(tree==NULL){
		tree=(struct node*)malloc(sizeof(struct node));
		tree->left=tree->right=NULL;
		tree->data=x;
		tree->height=0;
		return tree;
	}
	else if(xdata){
		tree->left=Insert(tree->left,x);
		if(GetHeight(tree->left)-GetHeight(tree->right)==2){
			if(xleft->data)
				tree=SingleRotateWithLeft(tree);
			else
				tree=DoubleRotateWithLeft(tree);
		}
	}
	else if(x>tree->data){
		tree->right=Insert(tree->right,x);
		if(GetHeight(tree->right)-GetHeight(tree->left)==2){
			if(x>tree->right->data)
				tree=SingleRotateWithRight(tree);
			else
				tree=DoubleRotateWithRight(tree);
		}
	}
	return tree;
}
int main(){
	struct node* AVLTree=NULL;
	int num[16]={3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
	for(int i=0;i<16;i++){
		AVLTree=Insert(AVLTree,num[i]);
	}
	InOrderTrversal(AVLTree);
	return 0;
}

AVL树也有删除操作，按照二叉搜索树的删除方法即可，同时删除路径上要维护AVL树的性质，代码暂时略

AVL树也可以基于数组实现（封装或者不封装），代码略