蓝桥杯 格子刷油漆
你可以从任意一个格子刷起,刷完一格,可以移动到和它相邻的格子(对角相邻也算数),但不能移动到较远的格子(因为油漆未干不能踩!)
比如:a d b c e f 就是合格的刷漆顺序。
c e f d a b 是另一种合适的方案。
当已知 N 时,求总的方案数。当N较大时,结果会迅速增大,请把结果对 1000000007 (十亿零七) 取模。
这一题卡了我半天,于是在查了资料和看了一些大神的代码后终于通过,然后来分享一些这题解法
首先解题思路是进行模拟,从一个格子开始向其他格子刷并且计算各种情况
开始的格子一共有两种情况,一是从四角落格子开始刷,二是从中间开始刷
第一种情况如下图的起点
遍历的可能情况有三种
一是从当前格子出发返回纵向相邻的格子【如a出发返回b,e出发返回f】
下图为一个例子【内含两种路线,acefdb,acfedb】
在这种情况里比如以a为起点可以走的横向相邻的格子有两种可能即c或d,假如选择走c那么想要最后回到b需要遍历完其他格子然后回到d才可以【则可以设总列数为n,n-1个格子时从一个角落出发可以返回到纵向相邻格子的可能为b[n-1],则n个格子时从一个角落出发可以返回到纵向相邻格子的可能为2*b[n-1](易看出形成了一个递归,可以把遍历存起来,b[1]=1,这一个容易看出,如b[n]都可以求出)】
二是从当前格子出发先到纵向相邻的格子,然后遍历其他格子
下图为一个例子【内含两种路线,abdfec,abdcef】
在这种情况下比如以a为起点则必然先走纵向的格子b然后可能走得格子有c或d,然后可以余下格子为cdef,又是从c或d开始走可以看成n-1个列格子,然后从角落开始走【则可以设总列数为n,n-1个格子时从一个角落出发的总可能是a[n-1],则n个格子时从一个角落出发先到纵向相邻的格子,然后遍历其他格子的可能是2*a[n-1](2*a[n-1]的原因是可以去两个点c或d,因此乘以2)(易看出也形成了一个递归,可以把遍历存起来各个a[n],a[1]=1,a[2]=6,这两个数据需要手动数)】
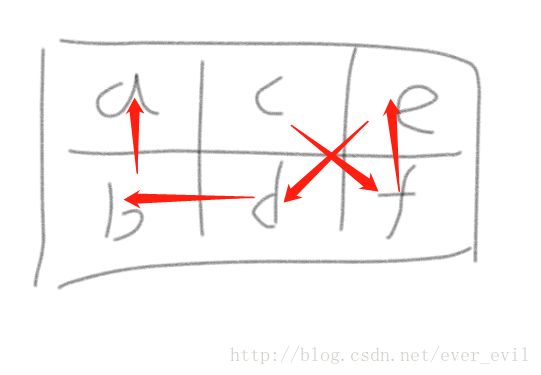
三为从当前格子出发然后到横向相邻的格子,然后返回初始格子的纵向相邻格子
下图为一个例子【acbdef因为这个图比较复杂画两个例子比较难看,因此不列两个例子】
这种情况下假如有n列,以a为起点可以选择走c或者d先,然后回到b再走另一个d或者c,则余下的点只剩n-2列并且起点为e或者f,可以看成n-2个列格子,然后从角落开始走【则可以设总列数为n,n-2个格子时从一个角落出发的总可能是a[n-2],则n个格子时从一个角落出发然后到横向相邻的格子,然后返回初始格子的纵向相邻格子,然后遍历其他格子的可能是4*a[n-2](4*a[n-1]的原因是一开始可以去两个点c或d,然后可以选择两个点e或者f,因此乘以2)(易看出也形成了一个递归,可以把遍历存起来各个a[n],a[1]=1,a[2]=6,这两个数据需要手动数)】
第二种情况如下图的起点
这种情况下一共有两种
一是先走左边然后再走右边遍历
如下图
这种情况下左边可能走的种数可以看作在左边的列数的情况下再以一个角落为起点然后需要返回自己纵向相邻的点的可能乘以2【因为可以走的有上下两个起点,如例子中的a,b】,然后再走右边的路,右边的格子可以看作在右边列数的情况下再以角落为起点的总可能数乘2【同上,因为可能的起点有两个,e或f】
【用上面例子中的数据可以知道,这种情况下计算的种数为,b[左边列数]*2+a[右边列数]*2】
二是先走右边再走左边
如下图
同上只是这种情况下计算数为【用上面例子中的数据可以知道,这种情况下计算的种数为,a[左边列数]*2+b[右边列数]*2】
最后也就是求n列时的总种数为,a[n]*4【四个角落开始的情况】+除去最左最右两个角落列外,每一个格子为起点的情况相加
具体代码如下
#include
using namespace std;
int main(){
int i,n;
long long int a[1001],b[1001],sum;
cin>>n;
a[1]=1;
b[1]=1;
a[2]=6;
b[2]=2;
for(i=3;i<=n;i++){
b[i]=(b[i-1]*2)%1000000007;
a[i]=(a[i-1]*2+b[i]+a[i-2]*2*2)%1000000007;
}
sum=a[n]*4;
for(i=2;i<=n-1;i++)
{
sum+=((b[n-i]*2*(a[i-1]*2))*2%1000000007+(b[i-1]*2*(a[n-i]*2)*2)%1000000007)%1000000007;
sum%=1000000007;
}
if(n==1)
sum=2;
cout< 值得注意的是
if(n==1)
sum=2;
这里是因为在只有一列的情况下是,没有四个角落,只有两个角落因此sum=a[n]*4;这一句代码会引起结果错误【不过在蓝桥杯测试里并没有测这一个数据】
还有一个值得注意的是这一段【画重点】
sum+=((b[n-i]*2*(a[i-1]*2))*2%1000000007+(b[i-1]*2*(a[n-i]*2)*2)%1000000007)%1000000007;
sum%=1000000007;
这一个取模是重点
最开始我的运算是
sum=(sum+(b[n-i]*2*(a[i-1]*2))*2+(b[i-1]*2*(a[n-i]*2)*2))%1000000007;
这样的然后小数据范围内是正确的,但是在大数据时一直是错误的
【这样的代码在蓝桥杯只能拿60分,过三组测试数据】
原因是在数据规模很大时,无论是进行加法还是乘法都可能超过数据范围,因此导致会出错
所以需要每一次运算都进行求余
在网络上有一些代码没有进行求余,因此是只能过部分测试数据的
这两个重点参加http://blog.csdn.net/u010126535/article/details/20651999此博客得出