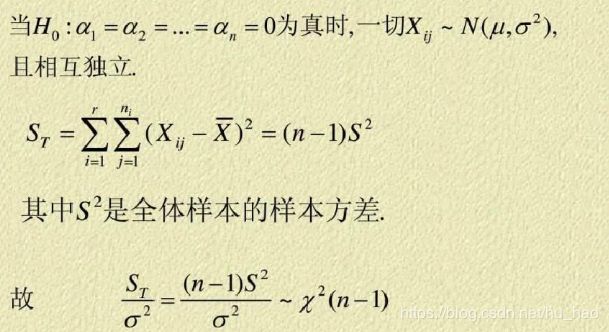概率统计方差分析-task04
概率统计方差分析
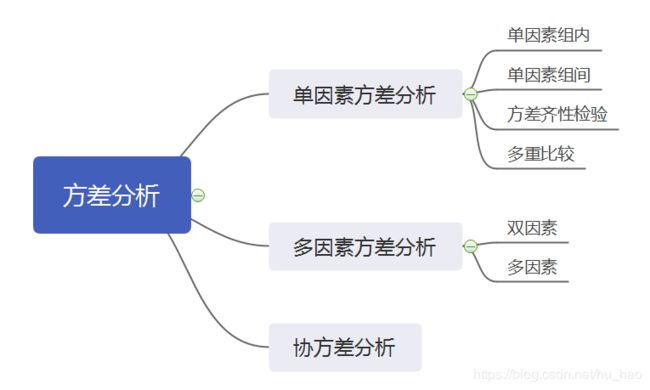
- 1.什么是方差分析
- 2 检验方法
- 2.1 基本原理
- 2.2 检验统计量
- 2.3 方差分析表
- 3.python实现
- 3.1 statsmodels方差分析
- 3.2 statsmodels 函数拟合
- 参考
1.什么是方差分析
一个指标有多个可能影响因素，每个因素有多个水平（为类别水平，非连续性数值），检验因素的水平不同对指标是否有影响时，称其为方差分析。这里如果因素的水平为连续值的话，可能就是回归分析了。
- 总结：指标为连续型变量，影响因素变化类型为类别变量，检验因数不同水平对指标是否有显著影响的方法，成为方差分析。
注意，方差分析方法是假设检验组内方差与组间方差是否有区别，方法存在原备假设及检验统计量。
方差分析可如下划分：
协方差分析
协方差分析将那些人为很难控制的控制因素作为协变量，并在排除协变量对观测变量影响的条件下，分析控制变量（可控）对观测变量的作用，从而更加准确地对控制因素进行评价。
方差分析中的原假设是：协变量对观测变量的线性影响是不显著的；在协变量影响扣除的条件下，控制变量各水平下观测变量的总体均值无显著差异，控制变量各水平对观测变量的效应同时为零。检验统计量仍采用F统计量，它们是各均方与随机因素引起的均方比。
2 检验方法
2.1 基本原理
- 方差分析的基本假定：
-
每个总体都应符合正态分布；
-
各个总体的方差σ2必须相同；
-
观测是独立的。
每个水平下指标分布为正态分布，这个好理解，受众多因素影响的量，其分布大多为正态分布。观测是独立的，个人理解是每个样本互不影响。那么方差为什么必须相同呢？
这是因为，我们所使用的统计量分布为F分布，分子分母均为卡方分布，而卡方分布的方差都为2n.
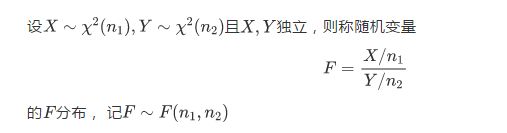
这告诉我们，在进行方差分析前，其实应该先进行方差齐次性检验。
可能有的小伙伴就要问了，老师老师，如果我对比了方差大小，发现各水平方差差异很大，那怎么办呢？
- 老师：这还用问，看看这几个字：方差分析的实质是检验多个水平的均值是否有显著差异，如果各个水平的观察值方差差异太大，只检验均值之间的差异就没有意义了
- 学生：你管这玩意，叫几个字？
是的，进行方差齐次性检验是增强我们对结果的信心，如果不进行，其实也可以，只是把报告交上去之后心里会比较虚。我这个结果可靠么，说服性强么，老板会接受么，会被开除么，花儿为什么是红的，时间会有终点么…
- 方差分析的原假设和备择假设：
设因素有k个水平，每个水平的均值为μ1,μ2,⋯,μk，检验均值是否相等，
H0:μ1=μ2=⋯=μk
H1:μ1,μ2,⋯,μk不全相等
在基本假定的条件下，如果原假设为真，则由4个总体抽取出来的4个样本均值的抽样分布应如图所示：
如果原假设不成立，则4个样本均值的抽样分布为：
2.2 检验统计量
检验统计量的构造通过将总体方差ST分解为组间方差SA，组内方差SE，有时候会多一个交互效应的方差，然后用组间均方差MSA跟组内均方差MSE相除，就得到了F检验统计量。
- 学生：真的假的，这么简单？
- 老师：是的，就是这么简单，不信看下面。
- 学生：你是第一个给我讲方差分析，还讲可赫伦分解定理的老师，ss老师，已经谢了。
- 学生卒，享年十八余六十月。
2.3 方差分析表
没有规矩，不成方圆，做方差分析时需要列出如下表格，是比较规范的做法。
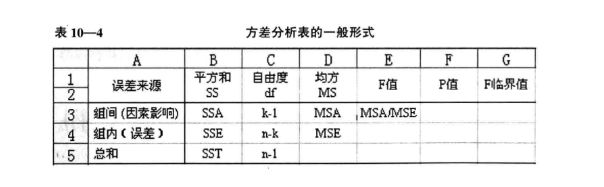
基本要素包括，方差来源列，写名称：因素A,因素B,因素C…。平方和SSA,SSB,SSC…，误差SSE,自由度，均方MSA,MSB,MSE,检验统计量MSA/MSE，MSB/MSE。其余的可能会加临界值和p值。
方差分析表举例2：
| 项目 | S S SS SS | 自由度 | M S MS MS | F F F比 | 显著性 |
|---|---|---|---|---|---|
| A A A | S S A SS_A SSA | k − 1 k-1 k−1 | M S A MS_A MSA | M S A / M S e MS_A / MS_e MSA/MSe | *, **, 或无 |
| B B B | S S B SS_B SSB | l − 1 l-1 l−1 | M S B MS_B MSB | M S B / M S e MS_B / MS_e MSB/MSe | |
| 误差 | S S e SS_e SSe | ( k − 1 ) ( l − 1 ) (k - 1) (l - 1) (k−1)(l−1) | M S e MS_e MSe | ||
| 总和 | S S SS SS | k l − 1 kl-1 kl−1 |
- 老师：你学会了么？
- 学生：哇，有模板！妈妈再也不用担心我的方差分析啦。
- 老师：。。。
3.python实现
3.1 statsmodels方差分析
python方差分析可以使用statsmodels中的stats.anova函数包
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
from statsmodels.graphics.api import interaction_plot, abline_plot
from statsmodels.stats.anova import anova_lm
#先构造数据集，这里我们构造一个两个因素的数据，为双因素组内方差分析
data = pd.DataFrame([[1, 1, 32],
[1, 2, 35],
[1, 3, 35.5],
[1, 4, 38.5],
[2, 1, 33.5],
[2, 2, 36.5],
[2, 3, 38],
[2, 4, 39.5],
[3, 1, 36],
[3, 2, 37.5],
[3, 3, 39.5],
[3, 4, 43]],
columns=['A', 'B', 'value'])
model = ols('value~C(A) + C(B)', data=data[['A', 'B', 'value']]).fit()
anovat = anova_lm(model)
print(model.summary())
print(anovat)
方差分析结果：
这里提示了数据量过小的问题。
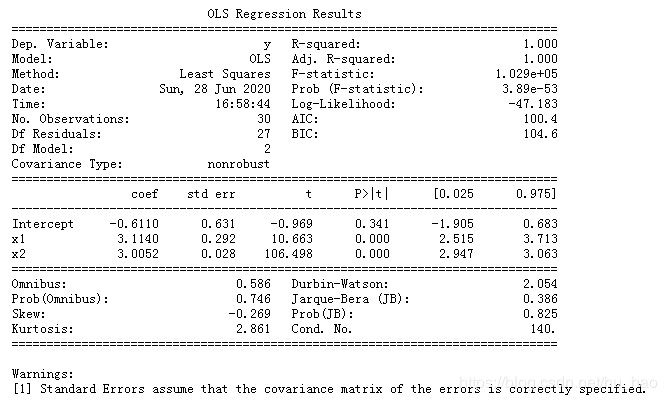
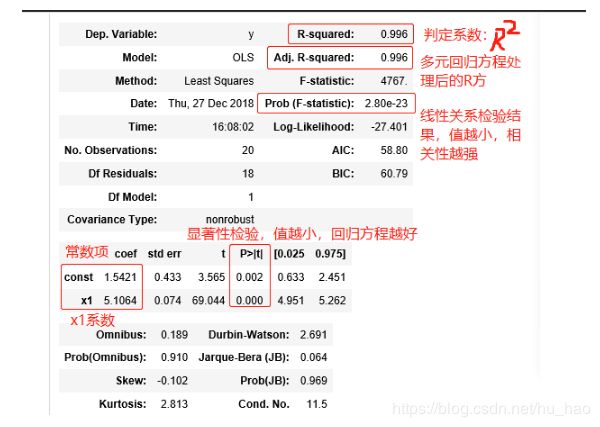
这里看下ols最小二乘模型拟合结果：
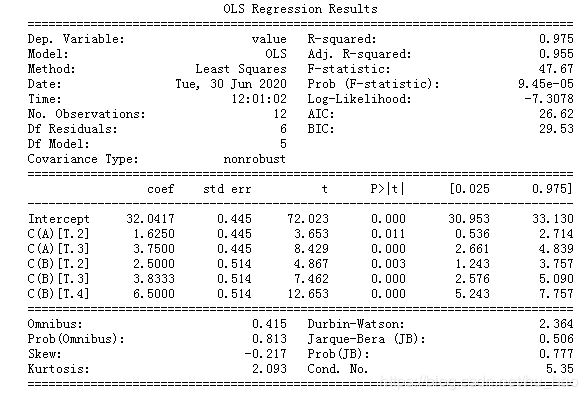
可以看出statsmodels的结果还是很专业美观的。
分析交互效应：
可以看出，上面的A,B主效应影响强烈，两者影响显著（P值均小于0.01）
接下来进行将交互效应添加进去，看交互效应影响结果。
model2 = ols('value~C(A) + C(B)+C(A):C(B)', data=data[['A', 'B', 'value']]).fit()
anova2=anova_lm(model2)
print(anova2)
#交互效应影响看不出来，不知怎么回事，F值都变为0了。
- 学生：为什么会有F=0呢？
- 老师：因为分析交互效应时，数据要求和不考虑交互效应是不一样的，这个数据中，对Ai,Bj水平下的数据只有xij一个，考虑交互效应时，xij需要有多组数据，不然计算SSA*B会有问题。这里只是举例函数用法，交互效应使用A:B表示。
- 学生：这次真的明白了！
3.2 statsmodels 函数拟合
import matplotlib.pyplot as plt
import statsmodels.api as sm
x=np.linspace(0,10,30)
x2=np.square(x)
y=3*x*x+3*x+np.random.normal(0,1,(30,))
df=pd.DataFrame({'y':y,'x1':x})
df['x2']=x2
model_new=ols('y~x1+x2',data=df).fit()
y_pred = model_new.predict(df['x1'])
fig = plt.figure()
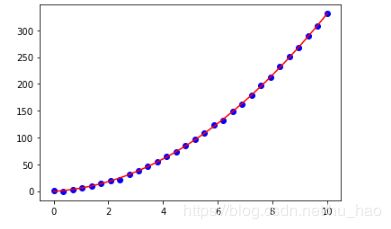
ax = fig.add_subplot(111)
ax.scatter(x, y, c='b')
ax.plot(x, y_pred, c='r')
plt.show()
print(model_new.summary())
拟合效果很棒。
- 评价结果说明
- 博主：码字不易，要求个赞，不过分吧。
- 游客：下次一定，下次一定
参考
1.方差分析
2.如何理解和使用方差分析？