Leetcode——1453. 圆形靶内的最大飞镖数量

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。

请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

示例 1：

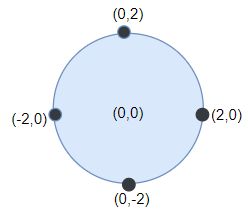
输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0,0) ，半径为 2 ，所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4 。

示例 2：

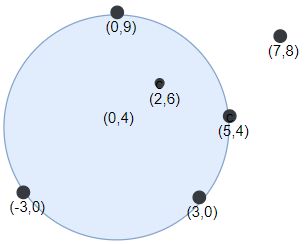
输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0,4) ，半径为 5 ，则除了 (7,8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5 。

示例 3：

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1
示例 4：

输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4

提示：

$1\le points.length\le 100$
$points[i].length==2$
$-10^4\le points[i][0],points[i][1]\le 10^4$
$1\le r\le 5000$

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard

题解

这算是一道几何题吧，首先考虑一个点的时候，这个时候只要点的距离$d<=r$的时候就可以被覆盖。
如果是两个点，那么只要满足$d(p_1,p_2)<=2\times r$就可以被圆覆盖，那么如果点的集合的个数大于2呢。
在原来覆盖两个点的基础上，我们要去覆盖一个新的点，如果我们不想舍弃这两个点，那么最极限的状态是什么呢？

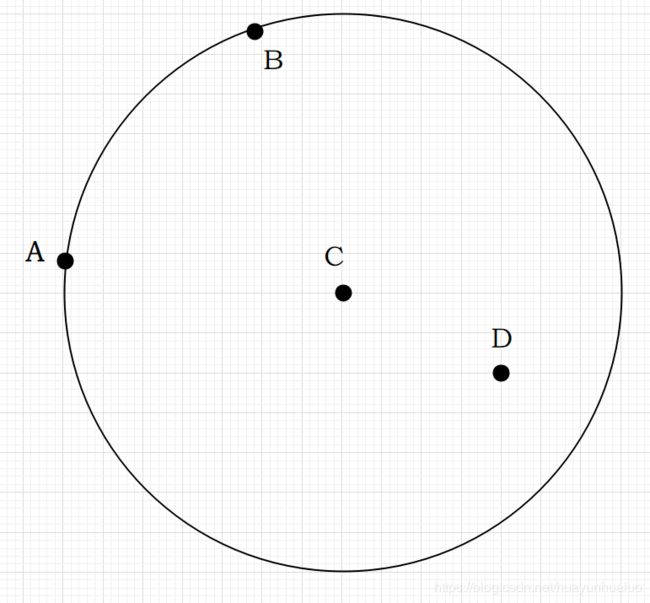
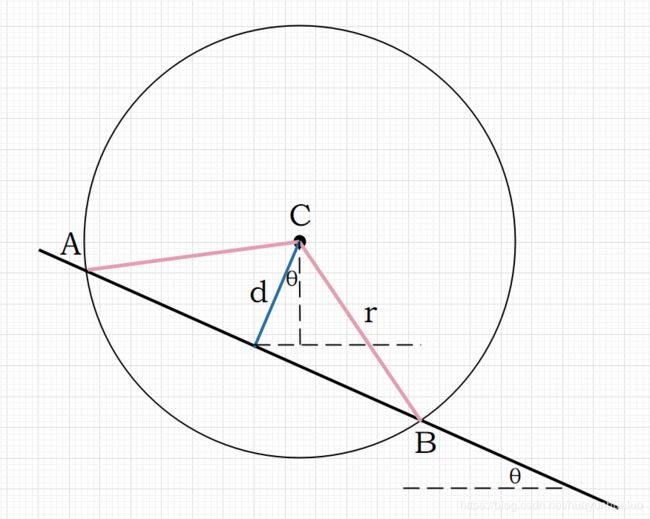
就是当两个点都是边上的时候，就是移动圆心的边界了，再移动就会失去这两个点。基于这个结论，我们可枚举两个点的集合情况，这两个点都是圆上的点，然后根据两个点的坐标推算出圆心的坐标，然后根据得到的圆去计算能够覆盖的点的个数。

那么如果得到圆心的坐标呢？

假设圆上的两个点为$A,B$,作为分别为$(x_a,y_a)$和$(x_b,y_b)$。那么我们可以得到直线AB的斜率，进而得到了$\theta$的值
$$\theta =\arctan (\frac{y_a-y_b}{x_a-x_b})$$

对于$AB$的中点的坐标为
$$mid=(\frac{x_a+x_b}{2},\frac{y_a+y_b}{2})$$
距离$d$表示为
$$d=\sqrt{r^2-distance(B,mid{)}^2}$$

那么对于C点 $x$的坐标为
$$x_c=x_{mid}+d\times sin(\theta )$$

同理可得
$$y_c=y_{mid}+d\times cos(\theta )$$

所以C点的坐标为$(x_{mid}+d\times sin(\theta ),y_{mid}+d\times cos(\theta ))$
然后去计算这个圆能够覆盖多少点就行，最后求最大值就是答案。

#define eps 1e-8

class Solution {
public:
    struct Point {
        double x,y;
        Point(){}
        Point(double tx, double ty) {x=tx; y=ty;}
        
    };
    double dist(Point p1,Point p2)
    {
	    return sqrt(pow(p1.x-p2.x,2)+pow(p1.y-p2.y,2));
    }

    Point GetCircleCenter(Point p1,Point p2,int r)
    {
	    Point mid = Point((p1.x+p2.x)/2,(p1.y+p2.y)/2);
	    double angle = atan2(p1.y-p2.y,p2.x-p1.x);
	    double d = sqrt(r*r-pow(dist(p1,mid),2));
	    return Point(mid.x+d*sin(angle),mid.y+d*cos(angle));
    }

    int max(int a,int b)
    {
	    if(a>b)
		    return a;
	    return b;
    }

    int numPoints(vector<vector<int>>& points, int r) {
        int n = points.size();
        int ans = 1;
        for(int i = 0;i<n;i++) {
            for(int j = i+1;j<n;j++) {
                Point p1 = Point(points[i][0],points[i][1]);
                Point p2 = Point(points[j][0],points[j][1]);
                if(dist(p1,p2) > 2.0*r) continue; 
                Point center = GetCircleCenter(p1,p2,r);
                int cnt = 0;
                for(int k =0;k<n;k++) {
                    Point pk = Point(points[k][0],points[k][1]);
                    if(dist(center,pk) < 1.0*r+eps) cnt++;
                }
                ans = max(ans,cnt);
            }
        }
        return ans;
    }
};