【SLAM】VINS-MONO解析——IMU预积分
4.IMU预积分
IMU预积分主要干了2件事,第一个是IMU预积分获得α、β、γ值,另一个是误差传递函数的获取。本部分的流程图如下图所示。

各个部分的讲解如下链接:
【SLAM】VINS-MONO解析——综述
【SLAM】VINS-MONO解析——feature_tracker
【SLAM】VINS-MONO解析——IMU预积分
【SLAM】VINS-MONO解析——vins_estimator
【SLAM】VINS-MONO解析——初始化(理论部分)
【SLAM】VINS-MONO解析——初始化(代码部分)
【SLAM】VINS-MONO解析——后端优化(理论部分)
【SLAM】VINS-MONO解析——后端优化(代码部分)
【SLAM】VINS-MONO解析——sliding window
【SLAM】VINS-MONO解析——回环检测
【SLAM】VINS-Fusion解析——流程
【SLAM】VINS-MONO解析——对vins-mono的修改使流程逻辑更清晰
【SLAM】VINS-MONO解析——基于vins-mono的slam系统开发
4.1 IMU预积分
这部分内容主要出现在vins_estimator/src/factor/integration_base.h中。
4.1.1 连续形式
第一个问题,为什么要IMU积分?
IMU获取的是加速度和角速度,通过对IMU测量量的积分操作,能够获得机器人的位姿信息。
IMU测量值包括加速度计得到的线加速度和陀螺仪得到的角速度。

其中 t下标表示在IMU坐标系下,并受到加速度偏置ba、陀螺仪偏置bw和附加噪声na、nw的影响。线加速度是重力加速度和物体加速度的合矢量,上标^代表是IMU的测量量,没有上标的值代表的是真实的量。
附加噪声是满足高斯噪声的。
![]()
加速度计偏置和陀螺仪偏置被定义为为随机游走并随着时间变化的,它的导数满足高斯分布。
![]()
对于图像帧k和k+1,体坐标系对应为bk和bk+1,位置、速度和方向状态值PVQ可以根据[tk,tk+1]时间间隔内的IMU测量值,在世界坐标系下进行传递的。

![]()
等号右边的三个量是IMU积分需要求的量,分别是bk+1时刻下,IMU坐标原点在世界坐标系上的坐标,速度和旋转角度,它们都是由bk时刻对应的值加上从bk到bk+1的变化量求得的,而这个变化量是由IMU积分获得的。
第二个问题,为什么要IMU“预”积分?
IMU的采样频率是高于图像帧的发布频率的,所以相邻两个图像帧之间的IMU信息需要积分从而与视觉信息对齐。
Rw<-t,也就是qw<-t,是需要被优化的量,而这个优化的量,是在IMU积分符号内部的,在后续的优化过程中,这个值是在不断的变化,所以需要一遍遍的重新IMU积分才能获得真正精确的PVQ值。为了减少IMU积分次数,就希望这个被优化的量不要出现在积分符号里,所以就采用IMU预积分的方式。把上面三个等式,全部等号两边乘以Rbk<-w,这样积分里面的内容只跟IMU的测量量有关,而与被优化的状态量无关,这就是IMU预积分。
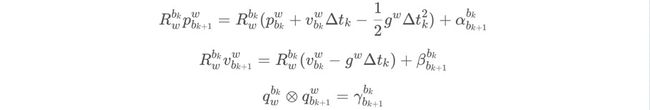
上式中,等号左边是要求的值,等号右边括号里的值是不需要积分的,也是能直接算出来的,α、β、γ是需要积分的量,也就是IMU预积分主要操作的值。
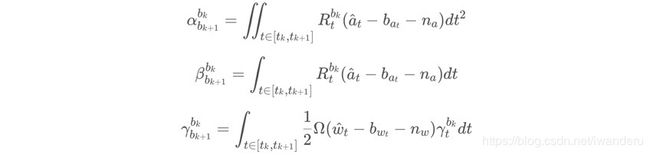
此时的积分结果α、β、γ可以理解为bk+1对bk的相对运动量,分别对应量纲为位移,速度和四元数。这里的α、β、γ可以用一阶泰勒展开来获取它们的近似值。
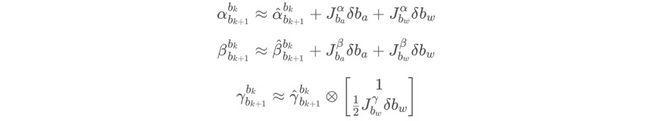
其中,带有^的量是由IMU测量量直接计算得到的。dba和dbw是bias的变化量,J是它们与α、β、γ对应的Jacobian。所以说要想求α、β、γ,我们需要首先分别求出它们由IMU测量量直接计算得到的标量值,然后再用bias进行修正获取真实值。
这一部分代码,见src/vins_estimator/estimator_node.cpp的evaluate()函数。
Eigen::Matrix<double, 15, 1> evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{//get IMU residuals Qi transform coordinate from i to w; Vi volosity at time i in w coordinate
Eigen::Matrix<double, 15, 1> residuals;
// O_P = 0,O_R = 3, O_V = 6, O_BA = 9, O_BG = 12
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);//0,9
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);//0,12
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);//3,12
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);//6,9
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);//6,12
Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;
//cuihuakun p6-(6) // IMU预积分的结果,消除掉acc bias和gyro bias的影响, 对应IMU model中的\hat{\alpha},\hat{\beta},\hat{\gamma}
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;
//ppt ch3-p69 // IMU项residual计算,输入参数是状态的估计值, 上面correct_delta_*是预积分值, 二者求'diff'得到residual.
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
return residuals;
}
4.1.2 离散形式

这一部分的目的是时刻求出从bk到bk+1时刻α尖,β尖、γ尖的值。从而α、β、γ提供一个初始值,等待后续被bias和相应的J进行修正。
如上图所示,IMU的采样频率要比feature_tracker_node的图像帧发布频率要高得多,分别对应着上图的红线和绿线。假设相邻的两根红线对应着i和i+1时刻,那么某一个delta_ti时间范围内,它的平均加速度,平均角速度分别是:
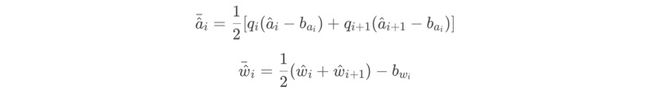
那么i+1时刻的PVQ分别是,
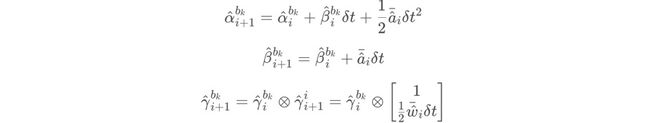
这个公式很明显可以用程序迭代的方式来计算,从第bk到bk+1时刻的值都能用这种方式递推获取。这部分代码在VINS里出现过多次。
第一次出现,见src/vins_estimator/estimator_node.cpp的pridict()函数。
void predict(const sensor_msgs::ImuConstPtr &imu_msg)
{ //获取当前时间
double t = imu_msg->header.stamp.toSec();
//首帧判断
if (init_imu)
{latest_time = t;init_imu = 0;return;}
//获取dt并传递时间
double dt = t - latest_time;
latest_time = t;
//获取当前时刻的IMU采样数据
double dx = imu_msg->linear_acceleration.x;
double dy = imu_msg->linear_acceleration.y;
double dz = imu_msg->linear_acceleration.z;
Eigen::Vector3d linear_acceleration{dx, dy, dz};
double rx = imu_msg->angular_velocity.x;
double ry = imu_msg->angular_velocity.y;
double rz = imu_msg->angular_velocity.z;
Eigen::Vector3d angular_velocity{rx, ry, rz};
//注意,以下数据都是世界坐标系下的
Eigen::Vector3d un_acc_0 = tmp_Q * (acc_0 - tmp_Ba) - estimator.g;
Eigen::Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - tmp_Bg;
tmp_Q = tmp_Q * Utility::deltaQ(un_gyr * dt);
Eigen::Vector3d un_acc_1 = tmp_Q * (linear_acceleration - tmp_Ba) - estimator.g;
Eigen::Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
tmp_P = tmp_P + dt * tmp_V + 0.5 * dt * dt * un_acc;
tmp_V = tmp_V + dt * un_acc;
//信息传递
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
第二次出现,见src/vins_estimator/estimator.cpp的processIMU()函数,分析见5.1.2-2。
第三次出现,见vins_estimator/src/factor/integration_base.h的midPointIntegration()的前半段。
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,const Eigen::Vector3d &_acc_1,
const Eigen::Vector3d &_gyr_1,const Eigen::Vector3d &delta_p,const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v, Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
{
Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);//after dt:qi+1
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);//average mid
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;//alpha(i+1)
result_delta_v = delta_v + un_acc * _dt;//beta(i+1)
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
}
4.2 误差传递矩阵
为什么要求误差传递函数?主要有2个目的,第一个是在求α、β、γ的值的时候给不同bias提供相应的Jacobian;第二个目的是给后端优化部分中IMU部分提供信息矩阵。
实际上讲,IMU在每一个时刻的测量都是有误差的,而且这个误差是满足的高斯分布的。在IMU预积分的递推过程中,由于下一时刻的值是由上一时刻的值再加上当前的测量值获得的,所以每一时刻的PVQ的计算值所对应的方差也是在不断累积。因此,求出对应的误差传递函数十分重要。
所以,根据误差传递函数的定义,我们可以建立一个下面这个形式的误差传递线性模型,它描述了下一时刻和当前时刻误差的关系:
![]()
dzk+1和dzk分别是下一时刻的误差和上一时刻的误差,上面这个等式对应的向量/矩阵表达式如下式所示:
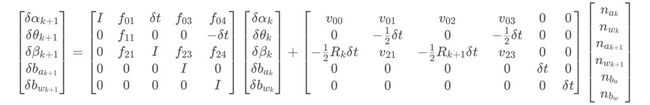
至于每一项的推导过程,请见参考文献中提供的链接。
Jacobian的迭代公式为:
![]()
这个J有了之后,带入4.1.1最后那个公式中去,就能得到真正的α、β、γ。注意的是,VINS里面出现过多次J的计算,一个是在这,另三个是在后端优化里出现,注意不要混淆。
协方差迭代公式为:
![]()
这个协方差矩阵,可以用于计算后端优化中IMU部分的信息矩阵。
噪声项的对角协方差矩阵Q为:
![]()
这一部分代码对应在midPointIntegration()的后半段,如下:
if(update_jacobian)
{ //这些量都是给F的填充作辅助
Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
Vector3d a_0_x = _acc_0 - linearized_ba;
Vector3d a_1_x = _acc_1 - linearized_ba;
Matrix3d R_w_x, R_a_0_x, R_a_1_x;
R_w_x<<0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;
R_a_0_x<<0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;
R_a_1_x<<0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;
//构造F矩阵
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
jacobian = F * jacobian;//used for cuihuakun p6-(6)
covariance = F * covariance * F.transpose() + V * noise * V.transpose();
4.3 IntegrationBase类的解读
这部分内容主要出现在vins_estimator/src/factor/integration_base.h中。
4.3.1 构造函数的定义
IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0, const Eigen::Vector3d &_linearized_ba,const Eigen::Vector3d &_linearized_bg)
: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
jacobian{Eigen::Matrix<double, 15, 15>::Identity()}, covariance{Eigen::Matrix<double, 15, 15>::Zero()},
sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}
{
noise = Eigen::Matrix<double, 18, 18>::Zero();//cuihuakun p9
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
}
这个构造函数读取了4个i时刻的初始值(共12个变量),
用_acc_0初始化acc_0和linearized_acc(分别是i时刻和bk时刻),
用_gyr_0初始化gyr_0和linearized_gyr(分别是i时刻和bk时刻),
用1515的单位矩阵初始化J,
用1515的0矩阵初始化协方差传递矩阵。
用yaml文件里读取的IMU噪声参数初始化18*18的噪声矩阵。
4.3.2 传播与重新传播
对应的函数分别是propagate()和repropagate()。
对于propagate()而言,它的使用次数更多,针对的是bk和bk+1内部的i时刻到i+1时刻的PVQ传播和误差传递。
void propagate(double _dt, const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1)
{
dt = _dt;
acc_1 = _acc_1; //a at time t=t+dt
gyr_1 = _gyr_1; //w at time t=t+dt
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
delta_p = result_delta_p; //alpha_i+1
delta_q = result_delta_q; //gama_i+1 from i+1 coordinate to bk
delta_v = result_delta_v; //beta_i+1
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
sum_dt += dt; //time for bk to bk+1
acc_0 = acc_1;//a_i+1 at bi+1 coordinate
gyr_0 = gyr_1;//w_i+1
}
对于repropagate()而言,它的使用次数较少,针对的是从bk到bk+1的PVQ传播矫正和误差传递矫正。
void repropagate(const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
{
sum_dt = 0.0;//the gap between IMU plot
acc_0 = linearized_acc;//a at bk in bk coordinate
gyr_0 = linearized_gyr;//w at bk in bk coordinate
delta_p.setZero();//alpha
delta_q.setIdentity();//gama trans bi to bk
delta_v.setZero();//beta
linearized_ba = _linearized_ba;
linearized_bg = _linearized_bg;
jacobian.setIdentity();
covariance.setZero();
for (int i = 0; i < static_cast<int>(dt_buf.size()); i++)
propagate(dt_buf[i], acc_buf[i], gyr_buf[i]);
}