poj-2184 Cow Exhibition 01背包变形-负数的处理(可扩展到dp处理负数问题?)
题目链接
poj-2184 Cow Exhibition
题目
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 15086 | Accepted: 6127 |
Description
fun..."
- Cows with Guns by Dana Lyons
The cows want to prove to the public that they are both smart and fun. In order to do this, Bessie has organized an exhibition that will be put on by the cows. She has given each of the N (1 <= N <= 100) cows a thorough interview and determined two values for each cow: the smartness Si (-1000 <= Si <= 1000) of the cow and the funness Fi (-1000 <= Fi <= 1000) of the cow.
Bessie must choose which cows she wants to bring to her exhibition. She believes that the total smartness TS of the group is the sum of the Si's and, likewise, the total funness TF of the group is the sum of the Fi's. Bessie wants to maximize the sum of TS and TF, but she also wants both of these values to be non-negative (since she must also show that the cows are well-rounded; a negative TS or TF would ruin this). Help Bessie maximize the sum of TS and TF without letting either of these values become negative.
Input
* Lines 2..N+1: Two space-separated integers Si and Fi, respectively the smartness and funness for each cow.
Output
Sample Input
5 -5 7 8 -6 6 -3 2 1 -8 -5
Sample Output
8
Hint
Bessie chooses cows 1, 3, and 4, giving values of TS = -5+6+2 = 3 and TF
= 7-3+1 = 5, so 3+5 = 8. Note that adding cow 2 would improve the value
of TS+TF to 10, but the new value of TF would be negative, so it is not
allowed.
Source
题意
牛分为2个属性,智力的搞笑力,值的范围都是[-1000,1000],牛的魅力值是该牛的智力和搞笑力的和,现在需要选N头牛参加比赛,要求分别求出智力和搞笑力的总值,以及魅力值,答案要求得到魅力值最大的情况值是多少。同时,在得到最大魅力值的情况下,智力总和和搞笑力总和都不能为负数。
题解
这个题其实第一眼看下去是能转化成01背包的模型的,主要的难点在负数的处理。关于01背包其实很好解决,2个值,把智力当做“背包空间”,搞笑力当做“价值”即可解决问题。如果不存在负数的情况下能够直接A题。
可是现在有负数呀,所以这个题博主也是墨迹了很长时间才看懂别人的博客(very vegetable),这里勉强分析一波:
首先考虑范围和负数的处理。如果我们想要将负数当做下标,最简单的方法就是扩大值的范围。例如:[-1000,1000],我们在储存的时候可以改成[0,2000],这样,[0,999]就是实际上的负数范围,1000就是0,[1001,2000]就是正数范围。所以,我们也可以分析出值的上限:100*1000*2,牛最多100头,每头牛最大值1000,负数部分转化。
然后数组就可以写出来了。现在考虑一下转化为01背包的模型。将智力ts[i](第i头牛的智力)当做“背包空间”,将搞笑力tf[i](第i头牛的搞笑力)当做“价值”。根据我们常用的01背包的状态转移方程,可以得到:
for(int j = M-1;j >= ts[i];j--){
dp[j] = Max(dp[j],dp[j - ts[i]] + tf[i]);
}M就是2*100*1000,。其实上面的方程就是我们不考虑正数的时候的状态转移方程。当然这个是滚动数组的优化版,如果看不懂就先看看简单的01背包是如何将二维数组优化成一维数组吧,安利一下“背包九讲”。
上面的转移方程可以看出,所谓的“价值”单单只考虑了搞笑力,但是题目要求魅力值是搞笑力和智力的总和。这里不用担心,最后遍历dp数组,将下标(智力)和值(搞笑力)相加就行了,判断下最大值而已。
上面分析的是正数,现在考虑一下负数。首先上代码:
for(int j = 0;j < M+ts[i];j++){
dp[j] = Max(dp[j],dp[j - ts[i]] + tf[i]);
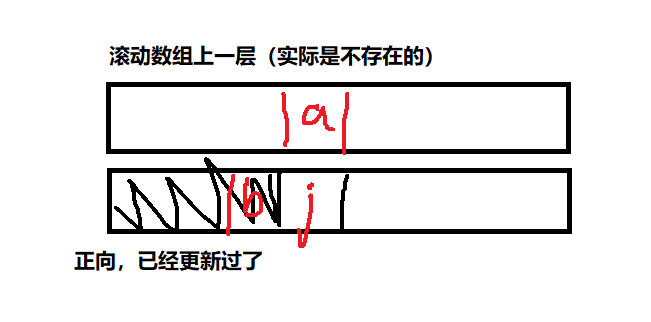
}可以看出循环是正向的,而不是负向!这里博主理解了好长时间啊!不过搞懂以后对01背包二维降一维的理解也更深刻了点。我们降到一维,最主要的原因就是dp[j]实际上是上一个状态的dp[j],我们状态转移方程就是将上一次状态转成当前状态。所以正数的时候我们要逆向,因为这样能确保遍历到dp[j]的时候我们获取的是上一个状态。负数亦然,j - ts[i],当ts[i]是正数,j - ts[i] < j,这样,如果我们正向推,得到的是下面这个图:
可以看出,a、b就是Max函数里面的两个变量,正向推的时候,b已经被更新了,不是上一个值,反向画逆序的图如下:
完美解决问题对吧,从而我们也能够理解负数的问题了。j - ts[i],由于ts[i]是负数,所以:j - ts[i] >j,所以状态转移时需要的2个值,不是一个上一个左,而是一个上一个右,所以我们只能这样操作:
所以就是要正向遍历了。
负数的问题解决后,整个dp数组都解决了。现在考虑的就是最大值问题。首先要求智力和搞笑力分别总和都不能是负数。也就是说,下标不为负,值不为负。所以智力的问题就很好解决了,下标 < 100*1000的全部不考虑,因为全是负数。值直接加个if语句判断一下喽,dp[i] < 0的全部不考虑。那么dp[i]的魅力值就是:dp[i] + i - 100*1000。注意,以为为了存负数,所以我们整体是加了100000的,实际上要减去这个值。遍历dp数组求答案即可。
C++ 258ms AC
#include
#include
#include
#include
#include
#include 一个小优化
上面分析的时候,主要代码都正确,但是在写状态转移方程的时候加了一个小小的优化,当值是-INF的时候说明是不考虑这个数的,所以直接跳过。不过实测优化不了多长时间,290ms降到260ms。。。。大家忽略吧。