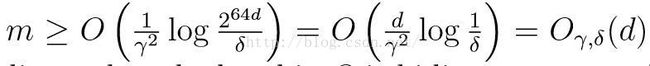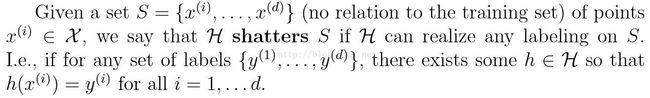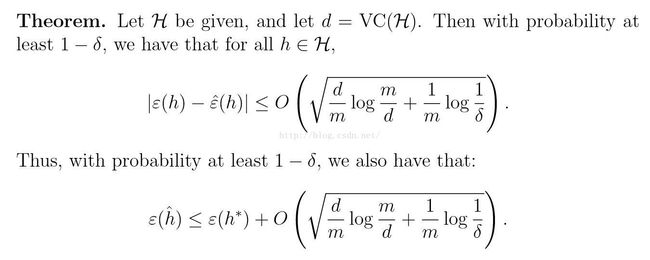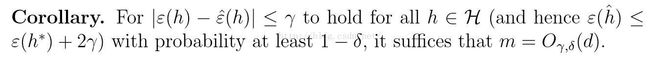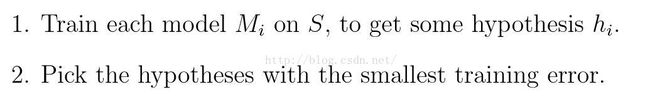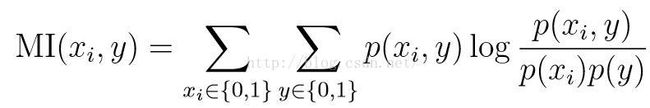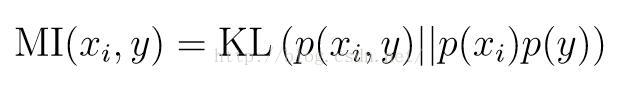【十】特征选择

无限假设集问题 The Case of Infinite H

在上一讲中我们讲解了有限假设集的情况，在这一讲中我们将把它扩展到无限假设集的情况上。

我们先思考一种直观的思路。假设我们有一个无限假设集，它被d个参数描述。当我们将其存在计算机中时，如果以双精度浮点格式存储，则存储一个数需要64 bit的空间，所以存储假设集中的一种假设就需要64d bit这么大的空间。由于计算机中一位只表示0和1，因此我们的“无限”假设集最多包含k=2^(64d)个假设。之所以由无限变为了有限，是因为计算机在存储过程中采用了一定的近似，相当于将连续值离散化了，并且表示的数的范围也是有限的。但我们提出这种思路只是为了更好的理解无限假设集如何将上一讲中得出的结论应用下来。将K带入上一讲最后的公式中，在保证准确率高于1-δ的情况下，我们有

由这一公式可以看出，我们所需要的训练样本数近似与参数个数成正比。上述这一模型比较特殊的两点在于：1）一个无限假设集不一定可以通过k=2^64d来表示；2）我们对参数没有一个严格的限制，即我们可以改变参数的个数实现同样的效果。为了克服上面的问题，我们先介绍下一定义。

给定集合S={x1,...,xd}，当假设集的假设可以处理S的任何一种标记情况时，我们称假设集H可以分离S，即对于任何标记{y1,...,yd}，一定存在假设集中的假设h可对所有i=1,...,d，使h(xi)=yi。即

在上述定义下，我们定义假设集的VC维（Vapnik-Chervonenkis Dimension）为假设集可分离的最大集合的规模，写为VC(H)。如何假设集H可分离任意大的集合，则称其VC(H)=∞。

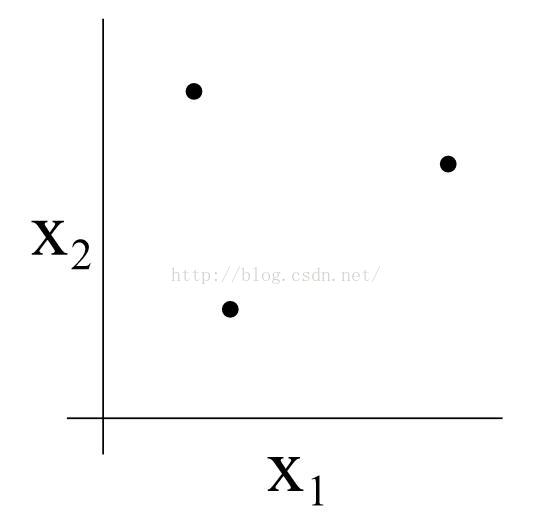
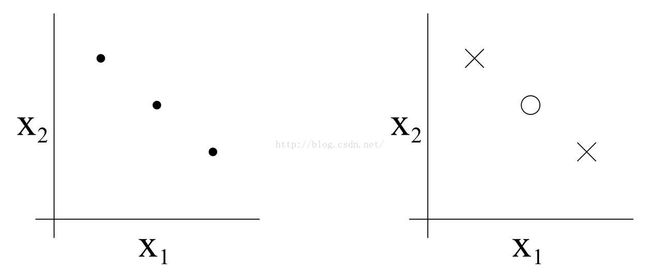
我们以一个有三个点的集合为例，如下图

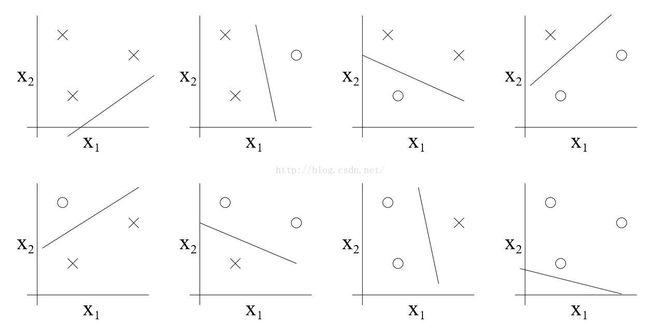
我们设定一个二维的线性分类假设集H。这一假设集能否将上述集合分类？答案是可以的，我们将证明如下。对于下列八种三个点的标记情况，我们都可在假设集中选择适当的假设，实现“零训练误差”。

但显然，二维的线性分类假设集无法分离任意四个点的集合，所以VC(H)=3。同时也应注意到，H并不是可分类任意一种三个点的集合，见下图。

所以如果我们想证明VC(H)至少为d，则我们只要给出一个可以被分类的d个样本的集合即可。

以上述结论为基础，我们将给出以下公式，这些公式可以认为是学习理论最重要的公式之一。

换句话说，如果一个假设具有有限的VC维，则只要样本数m足够大，一定会出现一致收敛。因此我们将给出一个上界。

所以，无限假设集所需的样本数与假设集的VC维成正比。总之，训练所需样本数与假设集参数个数成正比。

交叉验证法 Cross Validation

当我们选择参数时，我们会考虑选择几阶的函数来拟合（如logistic分类），或选择合适的惩罚因子达到较好的效果（l1正则的SVM）。我么们将如何自动的选择参数呢？

首先假设我们将从模型集合M={m1,...,md}中选择合适的模型。假设我们有训练集S，应用ERM算法，我们可以得到如下模型选择算法

显然这一算法基本无效，因为它追求最小的训练误差，必定会选择最复杂的模型。而最复杂的模型一定会带来很大的泛化误差。因此我们提出保留交叉验证算法Hold-out Cross Validation（也称为简单交叉验证算法Simple Cross Validation），算法的执行过程如下。

通过在训练集未使用过的集合Scv上测试，我们可以得到假设hi真实的泛化误差。一般而言，我们需要保留1/4-1/3的数据作为测试集，而30%是一个常见的选择。上述算法的第三步可以通过选择使ε_hatScv(hi)最小的模型i解得Mi，并在全部集合中训练Mi。保留交叉验证算法的缺点在于其“浪费”了将近30%的数据资源。为了不使数据浪费，我们可以使用k折叠交叉验证算法（K-fold Cross Validation），这一算法的过程如下

我们常常选择k=10，此时每一次训练只“浪费”了1/k这么大的数据，但我们需要对模型训练k次。当数据量很小时，我们采用去一交叉验证算法（Leave-one-out Cross Validation），此时k=m。

尽管我们介绍了上述多种版本的交叉验证算法，他们只能用于检验一些简单的模型。

特征选择 Feature Selection

另一个重要的模型选择算法称为特征选择算法。回忆我们之前介绍的文本分类算法，当我们选用字典作为向量时，其中有一些词对结果的影响很大，有一些对结果基本没有影响（如and、or等），我们需要找出哪些参数是对结果有重要影响的。下面将介绍一种搜索算法称为前向搜索Forward Search

上述这一算法称为封装模型特征选择Wrapper Model Feature Selection，因为它把我们选择出来的特征封装在一个集合里。与前向搜索方法相对应的，我们有反向搜索算法Backward Search。与前向搜索方法向集合中添加特征不同，反向搜索从原始特征集合中删除不需要的特征。

另一种特征选择方法称为过滤特征选择Filter Feature Selection，这一算法通过计算特征与结果的互信息量Mutual Information

选择其中符合要求的作为选取的特征。

//这里是分割线~
//顺便给自己的公众号打个广告，希望大家多多关注~
//关注我的公众号可以看到更多有意思的东西哦~