最短路径算法

问题描述：

最短路径问题是图论研究中的一个经典算法问题， 旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

所谓单源最短路径问题是指：已知图G=（V，E），我们希望找出从某给定的源结点S∈V到V中的每个结点的最短路径。
首先，我们可以发现有这样一个事实：如果P是G中从vs到vj的最短路，vi是P中的一个点，那么，从vs沿P到vi的路是从vs到vi的最短路。

最常用的路径算法有：Dijkstra算法、A*算法、SPFA算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法

以上是参考百度百科，以下分别论述闭包最短通路长度、Dijkstra算法和Floyd算法。

1.闭包最短通路长度

        定理：设G是带有相对于顶点顺序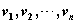的邻接矩阵A的图。从到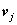的长度为r的不同通路的数目等于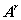的第（i,j）项，其中r为正整数。

其证明参考离散数学第六版，9.4.6。要理解这个过程也不难，可以从矩阵乘法原理去理解，从公式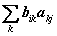上理解就是（i,j）=（i,k）*（k,j），如果是通路，它自然不为0了，相当于计数了。从这个定理可以看出，我们在计算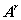时，如果（i,j）的值由0变成非0，此时就是两顶点之间通路长度，即需要至少分几段才能连接两点。最典型的应用是换乘次数最少的路径。

2.Dijkstra算法

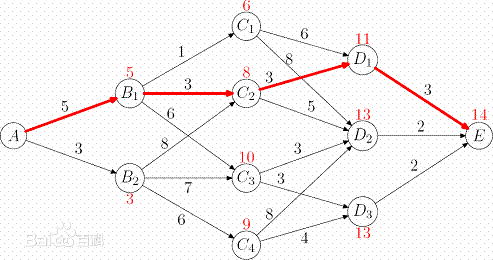
         Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

        算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

        算法步骤：
        a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则w正常有权值，若u不是v的出边邻接点，则w权值为∞。同时设每个顶点的最优值在L(u)中，L(vi)=无穷，L(起始点)=0;
       b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。
       c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。即L(v)=min(L(v),L(u)+w(u,v))
       d.重复步骤b和c直到所有顶点都包含在S中。

       理解起来也不是很难，就是从起始点开始，向周边找到最短距离，并记录到每个点，然后找到最短的路重新向周边找且记录。不过对于已经选择的最优点就不要重新计算了。

       为什么这么做，就能找出最优解呢，这里可以先看我的另一篇博文《动态规划-钢条切割》。里面提到，如果一个路径是最优到，那路径中的每一个点到终点也是最优的。同样，我们反过来走也是一样的。但这里和那里面又有点不一样，那里面是，一层一层地求最优解，即相隔1,2,3....点这样求，但实际上这没有广泛的适合性，当网络连接相当复杂时，你无法知道一点到另外一点的最优值，即使是相邻，如果你真的已经求出来了，恭喜你，你明白Dijkstra算法的精髓了。

        正因为我们时常不能很严格地将图分为一层一层的，所以要找到每一个点的最优解时，理解起来比较困难。那么我们怎么找到一个点的最优解呢，怎么样在不知道其它点的最优值时，求出这个点的最优解呢？其实我们人生也是如此，我们想每个选择都最优，其实很难做到。其实，只要大致方向上是对的，踏踏实实里往前走，时刻调整人生的方向，就能走上人生巅峰，迎娶白富美。这里有三个关键，一是大致方向上是对的，不能南辕北辙，二是踏踏实实，三是时刻调整。对，做到这三点很难做到吧，这个算法就教你怎么做到的。

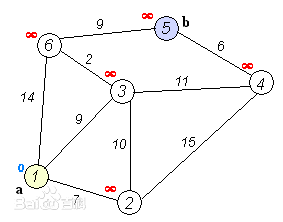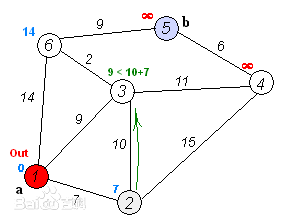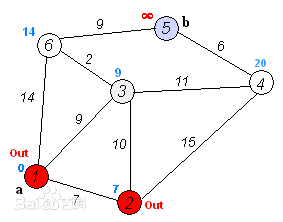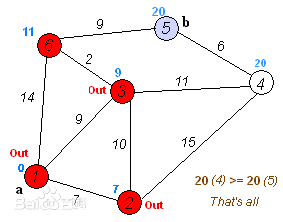
        首先，在起始点找到局部最优解（当然每个相邻点都要计算，你不尝试你怎么知道谁好谁坏呢？所以人生贵在敢于尝试，而且永远都不会忘记这种感觉，因为后面还要用到的），然后定位在那个点，这不难吧。图中标号为2就是，然后以这个点又找到局部最优解，点3。我们就会惊讶发现，原来从点2出发后，转了一圈发现点3又是最优的，说明点2的最优解的探索过程完了，7就是点2的最优解。既然找到了点2的最优解，自然以后就不管它喽，这就是算法中的集合S和U的作用。是吧，在外面转了一图，发现还是点3好，跟谈恋爱一样，虽说初恋不一定很优秀，但是最想念的哈。那我们继续从点3出发找最优解，发现点6是最优的，不过点6已经不是以前的点6了，因为它改了。既然点3不是最优的，说明点3的命运到头了，因为它不能继续保持领先地位，自然要让给下一位，同时点3也完成了自己最优解的使命了。

         这样，一步步地就把每个点的最优解求出来了，同时也不需要计算出每个点的所有情况再作比较，只需要证明它周边有比它更优秀的，来说明它不是所要找的最优路径中的点。同时也发现，它再怎么继续转悠，也不可能找到比它现在还小的数。有人就要问，这不是还没更新么，等之前的点更新之后，再反过来找此点，说不定能找到更小的。这看起来挺有道理的，其实不然，在局部的最优解中，其它的点即使是更新了最优值，同样要比此值要小，为什么呢，无论怎么更新，它始终要从它到初始点的最路径，加上某个值才使它进一步小，话说回来，它顶多是从别的点折返回来，就如点6还得从1-3，3-6给折回去，这样一来，怎么可能有1-2直接最优呢。所以呢，当转悠了一圈后，发现周边还有比我们强的，说明我们自己已经是最优的了，不需要去再去折腾了。这个时候，要么把棒子交给下一个人，要自己继续学习，使自己比以前的自己更强大才行，这就是我们平时说的，当才华不能支撑起野心时，是时候安静下来好好学习了。

         这里，还说一句，为什么这个算法不适合有负数的权值的呢？很简单，因为它依靠的是最优子序列所推测出来的，所以当存在负数时，这就不适用了。不然好不容易把了个最优的，发现下一个权值是负数，这说明上一个找的不是最优的，这不矛盾吗，是不是哈。

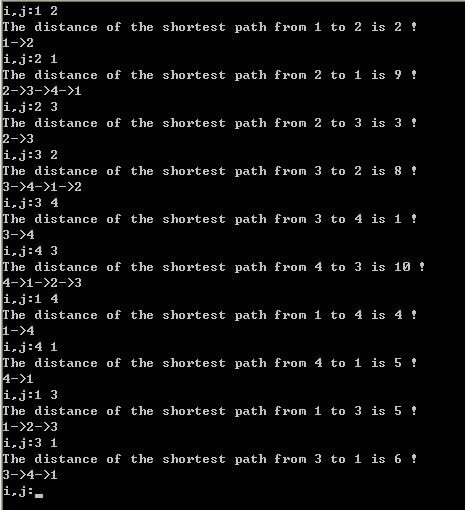
        那路径怎么确定呢？L(v)=min(L(v),L(u)+w(u,v))，每一次求每个顶点的最优值，都会产生一个u，即最优点的前一个点，如果这个顶点的值如果后面一直不变，那么它的前驱始终为u，但有改变，则它也改变，所以只要跟踪每一个点的前驱，按图索骥，就可以找到最优路径。

         说到这里，大家应该明白为什么要搞集合S和U了吧，下面就是C程序代码：

//path的每个值初始化为-1，后面打印时用的
int dijkstra(int **w,int *path,int n,int begin,int end)
{
	begin-=1;end-=1;
	int i;
	bool *S=new bool[n];//S,L与文章中的意义一样，这里没有U，因为U是S的余集
	int *L=new int[n];
	for(i=0;i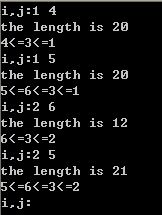
 
  
3.Floyd算法
 
  
 
     
         正如大多数教材中所讲到的，求单源点无负边最短路径用Dijkstra，而求所有点最短路径用Floyd。确实，我们将用到Floyd算法，但是，并不是说所有情况下Floyd都是最佳选择。     对于没有学过Floyd的人来说，在掌握了Dijkstra之后遇到All-Pairs最短路径问题的第一反应可能会是：计算所有点的单源点最短路径，不就可以得到所有点的最短路径了吗。简单得描述一下算法就是执行n次Dijkstra算法。 
         Floyd可以说是Warshall算法的扩展了，三个for循环便可以解决一个复杂的问题，应该说是十分经典的。从它的三层循环可以看出，它的复杂度是n3，除了在第二层for中加点判断可以略微提高效率，几乎没有其他办法再减少它的复杂度。 
         比较两种算法，不难得出以下的结论：对于稀疏的图，采用n次Dijkstra比较出色，对于茂密的图，可以使用Floyd算法。另外，Floyd可以处理带负边的图。   
   
 
        
   下面对Floyd算法进行介绍： 
     
   
 
           
    Floyd算法的基本思想：     可以将问题分解，先找出最短的距离，然后在考虑如何找出对应的行进路线。如何找出最短路径呢，这里还是用到动态规划的知识，对于任何一个城市而言，i到j的最短距离不外乎存在经过i与j之间的k和不经过k两种可能，所以可以令k=1，2，3，...，n(n是城市的数目)，在检查d(ij)与d(ik)+d(kj)的值；在此d(ik)与d(kj)分别是目前为止所知道的i到k与k到j的最短距离，因此d(ik)+d(kj)就是i到j经过k的最短距离。所以，若有d(ij)>d(ik)+d(kj)，就表示从i出发经过k再到j的距离要比原来的i到j距离短，自然把i到j的d(ij)重写为d(ik)+d(kj)，每当一个k查完了，d(ij)就是目前的i到j的最短距离。重复这一过程，最后当查完所有的k时，d(ij)里面存放的就是i到j之间的最短距离了。这样我们就可以用3个for循环就可以完成了。 
   
 
  
 
  
 
    
   
for ( int i = 0; i < 节点个数; ++i )
{
    for ( int j = 0; j < 节点个数; ++j )
    {
        for ( int k = 0; k < 节点个数; ++k )
        {
            if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
            {
                // 找到更短路径
                Dis[i][j] = Dis[i][k] + Dis[k][j];
            }
        }
    }
}
 
  
 
  
 
       但是这里我们要注意循环的嵌套顺序，如果把检查所有节点X放在最内层，那么结果将是不正确的，为什么呢？因为这样便过早的把i到j的最短路径确定下来了，而当后面存在更短的路径时，已经不再会更新了。具体来讲，这就是固定两端i,j，还是固定中间k的选择问题。这两个有什么区别呢。如果是固定两端，当k遍历完时，ij之间的最短距离就算完了，这对吗？很显然此时每个结点的最优值都还不确定呢，那结果就不一定对的，特别是算的越早的越不准。但如果我们把k固定，固定变化i,j，那么每一次都会把所有点经过k的点的最短距离算出来，当k算完，所有点的结果就算完了。这就是所有点对一个点的最小距离算完后，每个点都刷新一次，而前一种，每个点的刷新次数不一样，这公平吗？哈哈！
     接下来就要看一看如何找出最短路径所行经的城市了，这里要用到另一个矩阵P，它的定义是这样的：p(ij)的值如果为p，就表示i到j的最短行经为i->p...->j，也就是说p是i到j的最短行径中的j之前的第一个城市。P矩阵的初值为p(ij)=j。有了这个矩阵之后，要找最短路径就轻而易举了。对于i到j而言找出p(ij)，令为q，就知道了路径i->q->...->j；再去找p(qj)，再去找p(qj)，如果值为r，i到q的最短路径为q->r...->j；所以一再反复，到了某个p(tj)的值为j时，就表示t到j的最短路径为t->j，就会的到答案了，i到j的最短行径为i->q->r...->t->j。
      但是，如何动态的回填P矩阵的值呢？回想一下，当d(ij)>d(ik)+d(kj)时，就要让i到j的最短路径改为走i->...->k->...->j这一条路，但是d(kj)的值是已知的，换句话说，就是k->...->j这条路是已知的，所以k->...->j这条路上j的上一个城市(即p(kj))也是已知的，当然，因为要改走i->...->k->...->j这一条路，j的上一个城市正好是p(kj)。所以一旦发现d(ij)>d(ik)+d(kj)，就把p(kj)存入p(ij)。 
  
 
  
 
        可以这么想当d(ij)>d(ik)+d(kj)时，也就是说i->...->k->...->j,那么k应该在什么位置呢？我们知道path(i,j)一定由原先的值变化而来的，而且是由上一个path变化而来的，如果每一次变化都会造成i->k->...->j或i->...->k->j，这样的话，我们就可以递推得到我们所想要路径。那么如何才能这样，而不是i->...->k->...->j中间的任何一个呢？path(i,j)=path(?,?)呢？是path(i,k),还是path(k,j)？我们可以这么想，如果发生了d(ij)>d(ik)+d(kj)这么一个东西，抛开是不是最短的路径，但i,j,k之定通路，不仅是通路，而且，每次变化的路径是有一定的继承性的，因为它至少是经过第k点的最优路径。当k+1时，如果值没发生变化，则变化的是k~j而不是i~j，如果发生了变化了，说明上一个不是最佳的，需要调整。所以每次变化的一定是i->k->...->j或i->...->k->j。下面有一个例子说明：
 
  
 
  
 
   
 
  
 
  
 
         现在分析2~1之间的最短路径。k=1，2时，2到1之间的路径依然是无穷，因为是它们本身的节点，但此时别其它点已经计算到1，2暂时的最佳路径，比如3~1。当k=3时，2~3的路径计算出来，同时3~1的之前就计算出来了，所以些Path(2,1)=3。当k=4的时候，3~1的最佳路径发生变化，但与2~1的最佳无关，除非能够计算出来2~4~1的路径更短。如果你仔细思考的话，会发现如果path(i,j)只变化一次的话，那它的路径就是i~k~j,至于k~j是多少，那个是后续的事，如果变化了多次，它依然是i~k~j,因为些算法只计算2个长度的路径，所以每次的k一定会挨着i。会不会发生i~k,和k~j同时发生呢，会！但如果i~k发生了变化，那么k~j原先就会失效，得重新寻找更新了，所以从不变的角度来讲，i~k这个过程始终不会发生变化，这样我们可以通过寻找i~k~j,k~v~j,....找到我们所需要的路径。所以只需要将path(i,j)=path(i,k)这样赋值就可以了，如果是path(i,j)=path(k,j),这就和刚才分析是反过来了，同时初值做一次翻转。 
  
 
  
 
         上面解决了，那么path如何赋初值呢？那就看k=1是啥情况喽，很明显，Path(i,1)=1，因为i~1~1嘛，所以有path(i,j)=j。这样我们就得到其C语言程序了，如下： 
  
 
  
 
    
   
#define MAXLEN 10000
void initPath(int **path,int n)//初始化path
{
	for(int i=0;i";//打印原点
	int v=path[begin][end];//获得第一个路径顶点下标
	while(v!=end)//如果路径顶点下标不是终点
	{
		cout<";//打印路径顶点
		v=path[v][end];//获得下一个路径顶点下标
	}
	cout<
 
  
 
  
 
   
 
  
 
  
 
   
以上皆用到
 
   
 
    #define MAXLEN 10000
 
   
 
   
4.参考资料：
 
  
 
  
 
   http://developer.51cto.com/art/201403/433874.htm
 
  
 
  
 
   http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
 
  
 
  
 
   http://www.cnblogs.com/twjcnblog/archive/2011/09/07/2170306.html