ML实验：k-近邻概率密度估计方法

一 实验题目

二 算法分析

代码：

2.1

 
load('data3.mat')
 n=size(w,1);
 px=zeros(n,1);
 s=150;
 cen=zeros(s,1);
for i=1:s
    cen(i)=i*0.01;
end
 k=1;
 for j = 1:s
        for i = 1:n
 
        d(i) = abs(cen(j) - w(i));
        end
        t = sort(d);         % 对于距离排序
        m = find(d <= t(k)); % 找到满足要求的编号
        v=max(d(m));
        v=v^(-1);          
        p=k*0.1*v;         %计算概率密度函数   
        px(j)=p;
%         disp(px(j));
 end
   subplot(3,1,1);
   plot(cen,px ,'r-');
 
 
    k=3;
 for j = 1:s
        for i = 1:n
%             if i==j
%              d(i)=100;
%             else
        d(i) = norm(cen(j) - w(i));
%             end
        end
        t = sort(d); 
        m = find(d <= t(k));
        v=max(d(m));
        v=v^(-1);
        p=k*0.1*v;
        px(j)=p;
%         disp(px(j));
 end
   subplot(3,1,2);
   plot(cen ,px ,'g-');
      
 
    k=5;
 for j = 1:s
        for i = 1:n
%             if i==j
%              d(i)=100;
%             else
        d(i) = norm(cen(j) - w(i));
%             end
        end
        t = sort(d); 
        m = find(d <= t(k)); 
        v=max(d(m));
        v=v^(-1);
        p=k*0.1*v;
        px(j)=p;
%         disp(px(j));
 end
   subplot(3,1,3);
   plot(cen,px ,'y-');

2.2
 
load('data4.mat')
 n=size(w,1);
 px=zeros(n,1); 
  x=[-2:0.1:2];
  y=[-2:0.1:2];
   s=size(x,2);
   z=zeros(s,s);
 k=1;
 for j = 1:s
    for h=1:s
        for i = 1:n
        d(i) = sqrt((x(1,h) - w(i,1))^2+(y(1,j) - w(i,1))^2);
        end
        t = sort(d);          % 对于距离排序
        m = find(d <= t(k));  % 找到满足要求的编号
        v=max(d(m));
        v=(pi*v^2)^(-1);
        p=k*0.1*v;            %计算概率密度函数  
         z(h,j)=p;
    end
 end
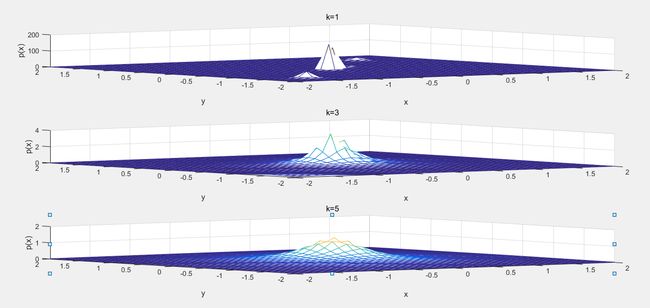
   subplot(3,1,1);
     mesh(x,y,z);
 
k=3;
 for j = 1:s
    for h=1:s
        
        for i = 1:n
        d(i) = sqrt((x(1,h) - w(i,1))^2+(y(1,j) - w(i,1))^2);
        end
        t = sort(d);
        m = find(d <= t(k)); 
        v=max(d(m));
        v=(pi*v^2)^(-1);
        p=k*0.1*v;
         z(h,j)=p;
    end
 end
   subplot(3,1,2);
     mesh(x,y,z);
     
     
     
     k=5;
 for j = 1:s
    for h=1:s
        for i = 1:n
        d(i) = sqrt((x(1,h) - w(i,1))^2+(y(1,j) - w(i,1))^2);
        end
        t = sort(d); 
        m = find(d <= t(k));
        v=max(d(m));
        v=(pi*v^2)^(-1);
        p=k*0.1*v;
         z(h,j)=p;
    end
 end
   subplot(3,1,3);
     mesh(x,y,z);
     
2.3

% function p = knn3(w,k,cen)
load('data2.mat')
[n yn]=size(w);
k=4;
for i=1:10
    w1(i,1)=w(i,1);
     w1(i,2)=w(i,2);
end 
 for i=11:20
    w2(i-10,1)=w(i,1);
     w2(i-10,2)=w(i,2);
 end 
for i=21:30
    w3(i-20,1)=w(i,1);
     w3(i-20,2)=w(i,2);
end 
 
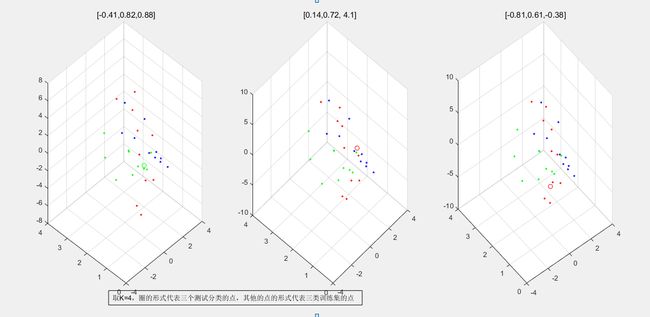
 cen = [-0.41,0.82,0.88];
        for i = 1:n
        d(i) = norm(cen(1,:) - w(i,:));
        end
        t = sort(d);          % 对于距离排序
        m = find(d <= t(k));  % 找到满足要求的编号
        v=max(d(m));
        v=((4/3)*pi*v^3)^(-1);
        p=k*0.3*v;             %计算概率密度函数 
        disp('[-0.41,0.82,0.88]的概率密度');
        disp(p);
        sum1 = length(find(m>0 & m<11));
        sum2 = length(find(m>10 & m<21));
        sum3 = length(find(m>20 & m<31));
        subplot(1,3,1);
 if (sum1 > sum2) || (sum1 > sum3)
    plot3(cen(1,1),cen(1,2),cen(1,3), 'ro');
     hold on;
    disp('该点属于第一类');
elseif (sum2 > sum1) || (sum2 > sum3)
  plot3(cen(1,1),cen(1,2),cen(1,3), 'go');
   hold on;
    disp('该点属于第二类');
elseif (sum3 > sum1) || (sum3 > sum2)
     plot3(cen(1,1),cen(1,2),cen(1,3), 'bo');
      hold on;
    disp('该点属于第三类');
else
    disp('无分类结果');
 end
% disp(w1(:,1));
        plot3(w1(:,1),w1(:,2),w1(:,3), 'r.');
        grid on;
        plot3(w2(:,1),w2(:,2),w2(:,3), 'g.');
        plot3(w3(:,1),w3(:,2),w3(:,3), 'b.');
       
        
     cen = [0.14,0.72, 4.1];
        for i = 1:n
        d(i) = norm(cen(1,:) - w(i,:));
        end
        t = sort(d); 
        m = find(d <= t(k)); 
        v=max(d(m));
        v=((4/3)*pi*v^3)^(-1);
        p=k*0.3*v;
        disp(' [0.14,0.72, 4.1]的概率密度');
        disp(p);
        
        sum1 = length(find(m>0 & m<11));
        sum2 = length(find(m>10 & m<21));
        sum3 = length(find(m>20 & m<31));
        subplot(1,3,2);
 if (sum1 > sum2) || (sum1 > sum3)
    plot3(cen(1,1),cen(1,2),cen(1,3), 'ro');
     hold on;
    disp('该点属于第一类');
elseif (sum2 > sum1) || (sum2 > sum3)
  plot3(cen(1,1),cen(1,2),cen(1,3), 'go');
   hold on;
    disp('该点属于第二类');
elseif (sum3 > sum1) || (sum3 > sum2)
     plot3(cen(1,1),cen(1,2),cen(1,3), 'bo');
      hold on;
    disp('该点属于第三类');
else
    disp('无分类结果');
 end
% disp(w1(:,1));
        plot3(w1(:,1),w1(:,2),w1(:,3), 'r.');
        grid on;
        plot3(w2(:,1),w2(:,2),w2(:,3), 'g.');
        plot3(w3(:,1),w3(:,2),w3(:,3), 'b.');
       
 
 
 cen = [-0.81,0.61,-0.38];
        for i = 1:n
        d(i) = norm(cen(1,:) - w(i,:));
        end
        t = sort(d); 
        m = find(d <= t(k)); 
        v=max(d(m));
        v=((4/3)*pi*v^3)^(-1);
        p=k*0.3*v;
        disp('[-0.81,0.61,-0.38]的概率密度');
        disp(p);
        
        sum1 = length(find(m>0 & m<11));
        sum2 = length(find(m>10 & m<21));
        sum3 = length(find(m>20 & m<31));
        subplot(1,3,3);
 if (sum1 > sum2) || (sum1 > sum3)
    plot3(cen(1,1),cen(1,2),cen(1,3), 'ro');
     hold on;
    disp('该点属于第一类');
elseif (sum2 > sum1) || (sum2 > sum3)
  plot3(cen(1,1),cen(1,2),cen(1,3), 'go');
   hold on;
    disp('该点属于第二类');
elseif (sum3 > sum1) || (sum3 > sum2)
     plot3(cen(1,1),cen(1,2),cen(1,3), 'bo');
      hold on;
    disp('该点属于第三类');
else
    disp('无分类结果');
 end
% disp(w1(:,1));
        plot3(w1(:,1),w1(:,2),w1(:,3), 'r.');
        grid on;
        plot3(w2(:,1),w2(:,2),w2(:,3), 'g.');
        plot3(w3(:,1),w3(:,2),w3(:,3), 'b.');
       

运行结果：

可以把每种情况的图单独画出来，我给的直接就是三种画到一起的。