组合优化中的P问题，NP问题，NP-complete问题和NP-hard问题

组合优化问题

组合优化是通过数学方法的研究去寻找离散事件的最优编排、分组、排序和筛选等，是运筹学中一个经典且重要的分支。对于一个极小化问题，问题描述如下式：
$$\begin{gathered} minf(x) \\ s.t.g(x)\ge 0 \\ x\in D \end{gathered}$$
f(x)是目标函数， g(x)是约束函数， x是可行解，D是包含有限个或无限个解的离散集合。所谓组合优化是指在离散的有限数学结构中寻找一个（或一组）满足给定约束条件并使目标函数值达到最小的解。因为现实生活里的大量优化问题是从有限个状态中选取最好的，所以大量的实际优化问题是组合优化问题。

计算复杂性

分析上面的定义，我们可以发现如果D是有限集合， 理论上只要遍历所有解空间，就能找到最优解。然而随着问题规模的扩大，D中解的个数会迅速增大，想要遍历所有整个解空间，几乎是不可能的。一般来说，组合优化问题通常带有大量局部极值点，往往是不可微、不可导、不连续、多维、多约束、高度非线性的NP问题。以旅行商问题为例：对于有n个城市的旅行商问题，所有可行路径有$\frac{(n-1)!}{2}$，若以路径比较为基本操作，则需要$\frac{(n-1)!}{2}-1$次基本操作才能保证找到最优解。对于每秒执行一百万次操作的计算机，当n=20时，需要1929年才能找到最优解。鉴于许多问题的求解复杂性远远大于旅行商问题，所以我们必须对计算复杂性理论有所了解，这也是最优化的理论基础。

算法或问题的复杂性一般表示为问题规模n的函数，时间复杂性记为T(n)， 空间复杂性记为S(n)。在算法分析和设计中，沿用实用性的复杂性概念，即把求解问题的关键操作（加减乘，比较等运算）指定为基本操作，而把算法执行基本操作的次数定义为算法的时间复杂性，算法执行期间占用的存储单元则定义为算法的空间复杂性。在分析复杂度时，可求出算法的复杂性函数p(n)，也可以用复杂性函数主要项的阶O(p(n))来表示。若算法A的时间复杂性为T(n)=O(p(n))，且p(n)为n的多项式函数，则称A为多项式算法，而把时间复杂度大于多项式时间的算法统统称为指数时间算法。

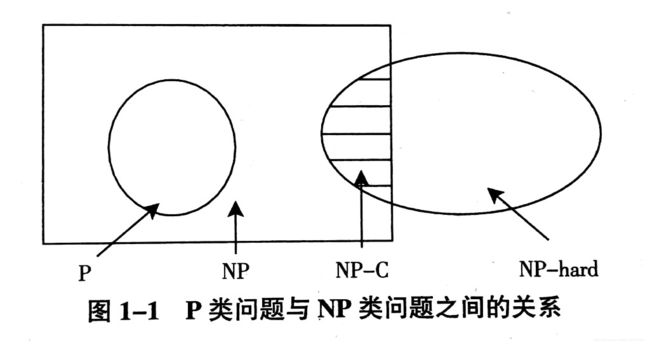
P类问题是具有多项式时间求解算法的问题类。但是迄今为止，许多优化问题没有找到求最优解的多项式时间算法。通常称比P类问题更广泛的问题为不确定多项式（Non-determinstic Polynomial, NP）问题，即NP问题。NP的概念可以由判定问题引入。

定义1：实例是问题的特殊表现，所谓实例就是确定了描述问题特性所有参数的问题，其中参数值称为数据，这些数据占用计算机的空间称为示例的输入长度。

定义2： 若一个问题的每个实例只有“是”与“否”两种答案，则称该问题为判定问题，并称肯定回答的实例为“是”实例，否定回答的实例为“否”实例。

定义3：若存在一个多项式函数p(x)和一个验证算法H, 对一类判定问题A的任何一个“是”的判定实例I都存在一个字符串S，S是I的“是”回答，满足其输入长度L(s)不超过p(L(I))，其中L(I)是I的输入长度，且验证算法验证S为I的“是”回答的计算时间不超过p(L(I))，则称判定问题A为NP问题。
【假使你得到了问题的解，我要验证你的解是否正确，我验证所花的时间是多项式，至于求解本身所花的时间是否是多项式我不管，可能有多项式算法，可能没有，也可能是不知道，这样的问题称为NP】

由此可见，判定问题是否输入NP的关键是对“是”的判定实例是否存在满足上述条件的一个字符串和算法，其中字符串可以理解为问题的一个解，而定义中没有强调字符串和算法是如何得到的。有上述定义可见$P\subset NP$, 但是否P=NP依然没有人能证明。归结和转换是描述问题特性的常用方法。如果能够将几类问题归结为一个问题， 一旦解决了一个归结后的问题，其他几类问题也就可以解决了。

定义4：给定问题$A_1$和$A_2$， 称$A_1$可多项式转换为$A_2$， 若存在一个多项式函数p(x)和一个字符串满足以下条件：

1. 对$A_1$的任何一个实例$I_1$，在其输入长度的多项式时间$p(L(I_1))$内构造$A_2$的一个实例$I_2$，使其长度不超过$p(L(I_1))$；
2. 由此构造使得实例$I_1$和$I_2$的解一一对应，且$L_1$为$I_1$的“是”回答的充要条件是$L_1$对应的解是$I_2$的一个“是”回答。

定义5：给定判定问题$A_1$和$A_2$，称$A_1$可多项式归约为$A_2$，若存在多项式函数p1(x)和p2(x)，使得对$A_1$的任何一个实例I。在多项式时间内构造$A_2$的一个实例，其输入长度不超过p1(L(I))， 并对$A_2$的任何一个算法H2， 都存在问题$A_1$的一个算法H1，使得H1调用H2且计算时间$f_{H1}(L(I))\le p2(f_{H2}(p1(L(I)))$.
【注：“问题A可约化为问题B”有一个重要的直观意义：B的时间复杂度高于或者等于A的时间复杂度。也就是说，NP问题不比NPC问题难。例如求解一元一次方程这个问题可以约化为求解一元二次方程，即可以令对应项系数不变，二次项的系数为0，将A的问题的输入参数带入到B问题的求解程序去求解。 另外，约化还具有传递性，A 可以化约为 B，B 可以约化为 C，那么 A 也可以约化为 C。 】

由此可见，若问题$A_2$存在多项式时间算法，则问题$A_1$一定存在多项式时间算法。进一步，我们给出NP-C和NP-hard的概念。

定义6：若$A\in NP$且NP中任何一个问题可以多项式归约为问题A，则判定问题$A\in NP-C(NP-complete)$。只要上述第二个条件成立，称问题A为NP-hard

由此可见，$NP-C\subset NP-hard$两者的区别仅在于NP-C必须判断问题属于NP类。同时，如果我们已知一个问题为NP-C或NP-hard，当遇到一个新问题时，若已知问题可多项式归约为新问题，则新问题为NP-hard，进而若克验证新问题属于NP类，则新问题为NP-C。

参考文献：

• 《物流配送车辆路径问题及其智能优化算法》
• 算法时间复杂度及P、NP、NP-Complete、NP-Hard问题
• NP-Hard问题浅谈