机器学习之使用plt绘制评价指标

 

目录

1绘制点状图

2.绘制某一列数据的分布图

3.绘制柱状图

4.绘制两两特征相关性热力图

5.箱线图

6.绘制AUC或者正确率等曲线

7seaborn中pairplot函数可视化探索数据特征间的关系 

8热力图

9.绘制特征与分类标签之间的分布图

---

1绘制点状图

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
%matplotlib inline
import matplotlib.pyplot as plt  # Matlab-style plotting
import seaborn as sns
color = sns.color_palette()
sns.set_style('darkgrid')
import warnings
def ignore_warn(*args, **kwargs):
    pass
warnings.warn = ignore_warn #ignore annoying warning (from sklearn and seaborn)


from scipy import stats
from scipy.stats import norm, skew #for some statistics


pd.set_option('display.float_format', lambda x: '{:.3f}'.format(x)) #Limiting floats output to 3 decimal points


fig, ax = plt.subplots()
ax.scatter(x = train['GrLivArea'], y = train['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()

2.绘制某一列数据的分布图

sns.distplot(train['SalePrice'] , fit=norm);

# Get the fitted parameters used by the function
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

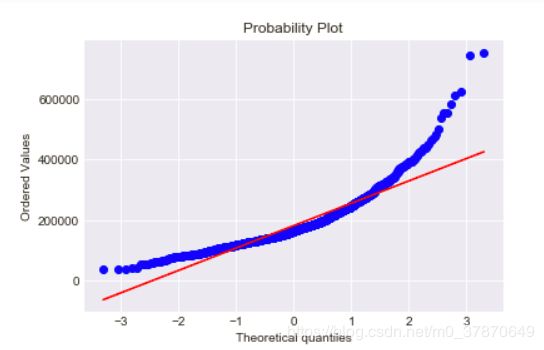
#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

mu = 180932.92 and sigma = 79467.79

 

#We use the numpy fuction log1p which  applies log(1+x) to all elements of the column
train["SalePrice"] = np.log1p(train["SalePrice"])

#Check the new distribution 
sns.distplot(train['SalePrice'] , fit=norm);

# Get the fitted parameters used by the function
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

mu = 12.02 and sigma = 0.40

3.绘制柱状图

f, ax = plt.subplots(figsize=(15, 12))
plt.xticks(rotation='90')
sns.barplot(x=all_data_na.index, y=all_data_na)
plt.xlabel('Features', fontsize=15)
plt.ylabel('Percent of missing values', fontsize=15)
plt.title('Percent missing data by feature', fontsize=15)

4.绘制两两特征相关性热力图

corrmat = train.corr()
plt.subplots(figsize=(12,9))
sns.heatmap(corrmat, vmax=0.9, square=True)

5.箱线图

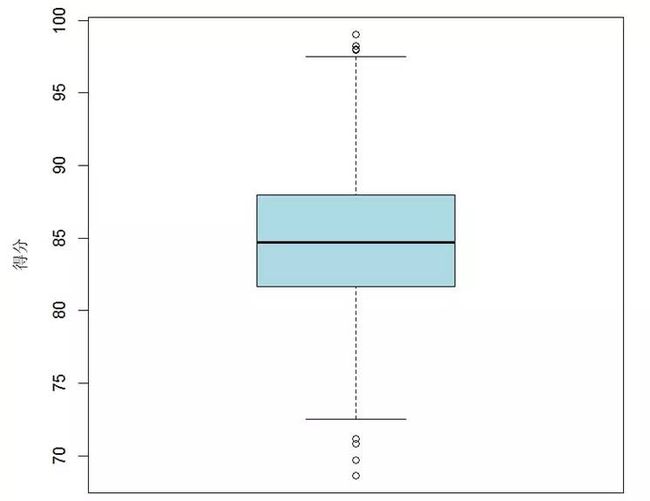
首先看一个长相标致的箱线图。水妈模拟了一个样本数据，是学生期末考试得分，箱线图如图1所示。

图1 学生期末考试成绩箱线图

看图说话，注意以下几个点：

箱子的中间一条线，是数据的中位数，代表了样本数据的平均水平。

箱子的上下限，分别是数据的上四分位数和下四分位数。这意味着箱子包含了50%的数据。因此，箱子的宽度在一定程度上反映了数据的波动程度。

在箱子的上方和下方，又各有一条线。有时候代表着最大最小值，有时候会有一些点“冒出去”。请千万不要纠结，不要纠结，不要纠结（重要的事情说三遍），如果有点冒出去，理解成“异常值”就好。

以上是解读箱线图最基本的三要素。虽然箱线图也能看分布的形态，但人们更习惯从直方图去解读分布的形态，而非箱线图。在了解了箱线图之后，我们今天着重讲两个事情。

第一件事情，不是所有的数据都适合画箱线图，不信，请看学生画的丑图。

图2 丑图示例

这几组箱线图看着不舒服，主要原因是，箱子被压得很扁，甚至只剩下一条线，同时还存在着很多刺眼的异常值。这种情况的出现，有两个常见的原因。第一是，样本数据中，存在特别大或者特别小的异常值，这种离群的表现，导致箱子整体被压缩，反而凸显出来这些异常；第二是，样本数据特别少，数据一少，就有可能出现各种诡异的情况，导致统计图长得对不起观众。

如果你画出的箱线图是这样的，那么有两个解决办法。第一，如果数据取值为正数，那么可以尝试做对数变换。对数变换水妈必须墙裂推荐，称得上画图界的整容神器，专治各种不对称分布、非正态分布和异方差现象等。图3就是整容前后的一组箱线图。你说我不想做变换，那么可以采取第二种解决办法，那就是，不画箱线图。

图3 对数变换前后的箱线图

以上是第一点要说明的，不是所有数据都适合画箱线图。第二点要说明的，更加重要的，那就是箱线图应该怎么用。答案是，配合着定性变量画分组箱线图，作比较！分组箱线图是水妈最喜欢的统计画图工具，没有之一。

如果只有一个定量变量，很少用一个箱线图去展示其分布，而是更多的选择直方图。箱线图更有效的使用方法，是作比较。我们举两个栗子。

第一个例子，我上课经常讲。假设我现在要比较男女教师的教学评估得分，用什么工具最好。答案是箱线图。没有比较就没有伤害，大家看图4能够明显感觉到箱线图是更有效的工具，能够从平均水平（中位数），波动程度（箱子宽度）以及异常值对男女教师的教学评估得分进行比较，而直方图却做不到。

图4 进行比较时，箱线图是更有效的工具

代码：

sns.boxplot(y = target)
Out[8]:

target.skew() #target数据的分布偏差较大

Out[10]:

1.8828757597682129

6.绘制AUC或者正确率等曲线

auc=np.array([0.63,0.65,0.67,0.68,0.70,0.73,0.733])
auc=list(auc)
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(auc, label='pred')
plt.legend()
_ = plt.ylim()
print(auc)

[0.63, 0.65, 0.67, 0.68, 0.7, 0.73, 0.733]

7seaborn中pairplot函数可视化探索数据特征间的关系 

seaborn中pairplot函数可视化探索数据特征间的关系，案例使用数据集为波士顿房价数据集。
 

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
 
# 读取数据
df = pd.read_csv('boston.csv', sep=',')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
              'NOX', 'RM', 'AGE', 'DIS', 'RAD',
              'TAX', 'PTRATIO', 'LSTAT', 'MEDV']
print(df.head())
 
# 利用探索新数据分析工具可视化特征两两间的广西
sns.set(style='whitegrid', context='notebook')
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], size=2.5)
plt.show()
 

 
可视化效果图：

8热力图

数据接7中的数据

# 可视化相关系数矩阵，理论：皮尔逊相关系数
cm = np.corrcoef(df[cols].values.T)
sns.set(font_scale=1.5)
hm = sns.heatmap(cm,
                 cbar=True,
                 annot=True,
                 square=True,
                 fmt='.2f',
                 annot_kws={'size':15},
                 yticklabels=cols,
                 xticklabels=cols)
plt.show()

 

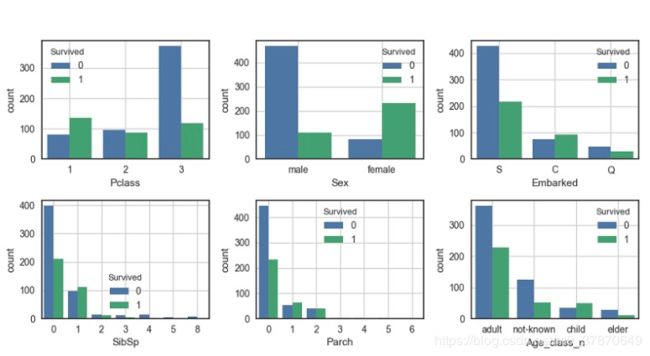
9.绘制特征与分类标签之间的分布图

 

#---------- analysis the mapping feature to result  ----------#
sns.set(style = 'white')
fig = plt.figure()

# Pclass
plt.subplot2grid((3,3),(0,0))
ax = sns.countplot(x = 'Pclass', hue = 'Survived', data = df_train)
# plt.title('Pclass')
# plt.xlabel('Pclass') 
# plt.ylabel('count')
plt.grid(True)
# plt.show()

# Sex
plt.subplot2grid((3,3),(0,1))
ax = sns.countplot(x = 'Sex', hue = 'Survived', data = df_train)
# plt.title('Sex')
# plt.xlabel('Sex') 
# plt.ylabel('count')
plt.grid(True)
# plt.show()

# Embarked
plt.subplot2grid((3,3),(0,2))
ax = sns.countplot(x = 'Embarked', hue = 'Survived', data = df_train)
# plt.title('Embarked')
# plt.xlabel('Embarked') 
# plt.ylabel('count')
plt.grid(True)
# plt.show()

# SibSp
plt.subplot2grid((3,3),(1,0))
ax = sns.countplot(x = 'SibSp', hue = 'Survived', data = df_train)
# plt.title('SibSp')
# plt.xlabel('SibSp') 
# plt.ylabel('count')
plt.grid(True)
# plt.show()

# Parch
plt.subplot2grid((3,3),(1,1))
ax = sns.countplot(x = 'Parch', hue = 'Survived', data = df_train)
# plt.title('Parch')
# plt.xlabel('Parch') 
# plt.ylabel('count')
plt.grid(True)
# plt.show()