RBF网络逼近算法（matlab）——S-Function函数实现

RBF网络原理

RBF网络原理同BP网络类似，具体原理及公式推导下次更新，这里先简单说明。
不同的是RBF网络的激活函数使用的是高斯基函数（其值在输入空间中有限范围
为非零值），而不是Sigmoid函数（其值在输入空间中无限范围为非零值）。

咋们直接上例程

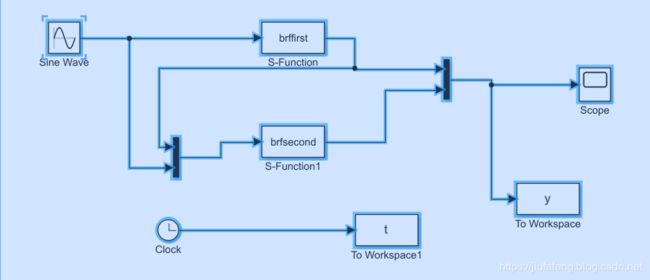
主程序

其中s-function是加入下面的两个主程序，to workspace需要设置变量名称（variable）还有储存形式（save fromat），如下

%%%%rbf逼近部分程序——brffirst.m
%S-function标准开头部分，sys含义下面结合flag变量讨论，x0状态变量的初始值，
str保留参数（没有什么意义，置空就行），ts（1）采样周期-ts（2）偏移量，t则指当
前仿真采样时间，x状态向量，u输入变量，flag状态标志
function [sys,x0,str,ts]=brffirst(t,x,u,flag) 
%判断当前所处状态
switch flag
    case 0
[sys,x0,str,ts]=mdlInitializeSizes;  %flag==0时，参数初始化
    case 1
sys=mdlDerivatives(t,x,u);           %flag==1时，计算其微分
    case 3
sys=mdlOutputs(t,x,u);               %flag==2时，计算其输出
    case{2,4,9}
    sys=[];
    otherwise                        %错误情况处理
    error(['Unhandled flag=',num2str(flag)]);
end

function[sys,x0,str,ts]=mdlInitializeSizes
%这部分需要根据实际输入输出设定
sizes=simsizes;                   	  %设置模块参数结构体
sizes.NumContStates =2;               %模块连续变量个数
sizes.NumDiscStates =0;      		  %模块离散变量个数
sizes.NumOutputs    =1;      		  %模块输出变量个数
sizes.NumInputs     =1;      		  %模块输入变量个数
sizes.DirFeedthrough=0;      		  %模块是否前后贯通，输入是否能直接控制输出
sizes.NumSampleTimes=0;      		  %模块采样时间

sys=simsizes(sizes);      		      %模块设置完成后传递给sys参数
%这部分是根据需要逼近的函数设置初始化变量
x0=[0,0];
str=[];
ts=[];
function sys=mdlDerivatives(t,x,u)
sys(1)=x(2);
sys(2)=-25*x(2)+133*u;
function sys=mdlOutputs(t,x,u)
sys(1)=x(1);

%%%%%rbf网络构建部分程序——brfsecond.m
function [sys,x0,str,ts]=brfsecond(t,x,u,flag)
switch flag
    case 0
[sys,x0,str,ts]=mdlInitializeSizes;
    case 3
sys=mdlOutputs(t,x,u);
    case{2,4,9}
    sys=[];
    otherwise
    error(['Unhandled flag=',num2str(flag)]);
end

function[sys,x0,str,ts]=mdlInitializeSizes
sizes=simsizes;
sizes.NumContStates=0;
sizes.NumDiscStates=0;
sizes.NumOutputs  =1;
sizes.NumInputs    =2;
sizes.DirFeedthrough=1;
sizes.NumSampleTimes=0;
sys=simsizes(sizes);
x0=[];
str=[];
ts=[];

function sys=mdlOutputs(t,x,u)
%这部分是设定高斯核ci，xite学习率，alfa动量因子，b高斯基函数宽度，其实理解了算法推到，这部分就很好理解了。
persistent w w_1 w_2 b ci
alfa=0.05; 
xite=0.5; 
if t==0
    b=1.5;
    ci=[-1 -0.5 0 0.5 1;
        -10 -5 0 5 10];
    w=rands(5,1);
    w_1=w; 
    w_2=w_1;
end
ut=u(1);
yout=u(2);
xi=[ut yout]';
for j=1:1:5
    h(j)=exp(-norm(xi-ci(:,j))^2/(2*b^2));
end
ymout=w'*h';
d_w=0*w;
for j=1:1:5
    d_w(j)=xite*(yout-ymout)*h(j);
end
w=w_1+d_w+alfa*(w_1-w_2);
w_2=w_1;
w_1=w;
sys(1)=ymout;

正确的出图需要simuling图设计正确，我开始连接那个图就出现了蛮多问题的：

1. 把rbf的网络结构和逼近函数搞反，导致各部分输入输出参数不匹配
2. 需要对to workspace模块设置，改为输出array格式，否成按时间输出则是1*1double，绘图时矩阵维度报错。

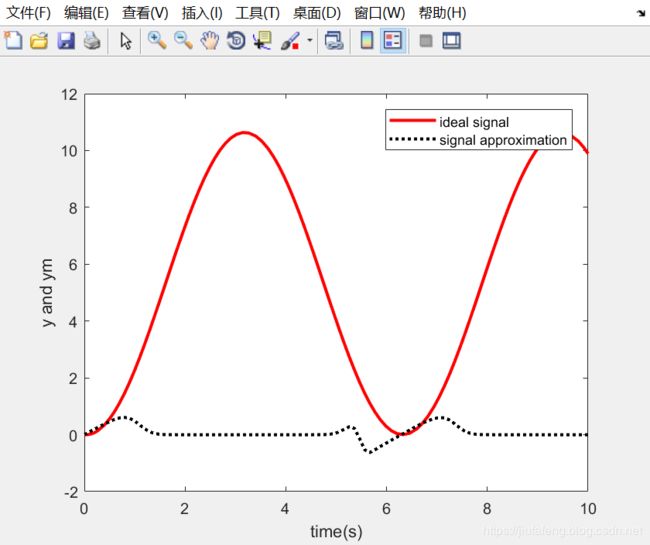
最后新建绘图程序

%%%%绘制逼近的函数曲线及误差
close all;
figure(1);
plot(t,y(:,1),'r',t,y(:,2),'k:','linewidth',2);
xlabel('time(s)');
ylabel('y and ym');
legend('ideal signal','signal approximation');

结果如下