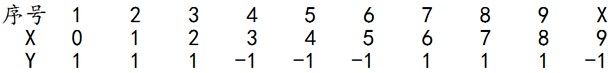AdaBoost 人脸检测介绍(4) : AdaBoost算法举例

　　本系列文章总共有七篇，目录索引如下：
　　AdaBoost 人脸检测介绍(1) : AdaBoost身世之谜
　　AdaBoost 人脸检测介绍(2) : 矩形特征和积分图
　　AdaBoost 人脸检测介绍(3) : AdaBoost算法流程
　　AdaBoost 人脸检测介绍(4) : AdaBoost算法举例
　　AdaBoost 人脸检测介绍(5) : AdaBoost算法的误差界限
　　AdaBoost 人脸检测介绍(6) : 使用OpenCV自带的 AdaBoost程序训练并检测目标
　　AdaBoost 人脸检测介绍(7) : Haar特征CvHaarClassifierCascade等结构分析

4. AdaBoost算法举例

4.1 实例1

　　下面我们举一个简单的例子来看看AdaBoost的实现过程：

　　图中，“+”和“-”分别表示两种类别，在这个过程中，我们使用水平或者垂直的直线作为分类器，来进行分类。
　　第一步：

　　根据分类的正确率，得到一个新的样本分布D_2，一个子分类器h_1。其中划圈的样本表示被分错的。在右边的图中，比较大的“+”表示对该样本做了加权。

　　也许你对上面的ε_1和α_1怎么算的不是很理解。下面我们算一下，只有自己把算法演算一遍，才会真正的懂这个算法的核心。算法最开始给了一个均匀分布 D 。所以h_1里的每个点的值是0.1。当划分后，有三个点划分错了，根据算法误差表达式得到误差为分错了的三个点的值之和，所以ε_1=(0.1+0.1+0.1)=0.3，而α_1根据表达式 的可以算出来为0.42. 然后就根据算法把分错的点权值变大。如此迭代，最终完成AdaBoost算法。

　　第二步：

根据分类的正确率，得到一个新的样本分布 D3 和一个子分类器 h2 。
　　第三步：

　　得到一个子分类器 h3 。
　　最后整合所有子分类器：

　　每个区域是属于哪个属性，由这个区域所在分类器的权值综合决定。比如左下角的区域，属于蓝色分类区的权重为 h1 中的0.42和 h2 中的0.65，其和为1.07；属于淡红色分类区域的权重为 h3 中的0.92；属于淡红色分类区的权重小于属于蓝色分类区的权值，因此左下角属于蓝色分类区。因此可以得到整合的结果如上图所示，从结果图中看，即使是简单的分类器，组合起来也能获得很好的分类效果。

　　Remark：本例中使用的权值更新公式与前面介绍的公式有一点点出入！

4.2 实例2

　　给定下列训练样本，请用AdaBoost算法学习一个强分类器。　　

　　求解过程：初始化训练数据的权值分布，令每个权值 w1i=1/N=0.1 ，其中 N=10,  i=1,2,⋯,N. 然后分别对于 m=1,2,3,⋯ 等值进行迭代。

　　拿到这10个数据的训练样本后，根据 X 和 Y 的对应关系，要把这10个数据分为两类，一类是“1”，一类是“-1”，根据数据的特点发现：“0 1 2”这3个数据对应的类是“1”，“3 4 5”这3个数据对应的类是“-1”，“6 7 8”这3个数据对应的类是“1”，9是比较孤独的，对应类“-1”。抛开孤独的9不讲，“0 1 2”、“3 4 5”、“6 7 8”这是3类不同的数据，分别对应的类是1、-1、1，直观上推测可知，可以找到对应的数据分界点，比如2.5、5.5、8.5 将那几类数据分成两类。当然，这只是主观臆测，下面实际计算下这个具体过程。

　　第一轮迭代：
　　对于 m=1 ，在权值分布为 D1 （10个数据，每个数据的权值皆初始化为0.1）的训练数据上，经过计算可得：
　　● 阈值 θ 取2.5时误差率为 0.3（x < 2.5时取1，x > 2.5时取-1，则6 7 8分错，误差率为0.3）；
　　● 阈值 θ 取5.5时误差率最低为 0.4（x < 5.5时取1，x > 5.5时取-1，则3 4 5 6 7 8皆分错，误差率0.6大于0.5，不可取。故令 x > 5.5 时取 1，x < 5.5时取-1，则0 1 2 9分错，误差率为0.4）；
　　● 阈值 θ 取8.5时误差率为0.3（x < 8.5时取1，x > 8.5时取-1，则3 4 5分错，误差率为0.3）。
可以看到，无论阈值θ取2.5，还是8.5，总得分错3个样本，故可任取其中任意一个如2.5，弄成第一个基本分类器为：

G1(x)={1,       x<2.5−1,    x≥2.5

　　上面说阈值 θ 取2.5时则6 7 8分错，所以误差率为0.3，更加详细的解释是：
　　● 0、1、2对应的类是1，它们本身都小于2.5，所以被 G1(x) 分在了类“1”中，分对了。
　　● 3、4、5对应的类是-1，它们本身都大于2.5，所以被 G1(x) 分在了类“-1”中，分对了。
　　● 但6、7、8本身对应类是1，却因它们本身大于2.5而被 G1(x) 分在了类”-1”中，所以这3个样本被分错了。
　　● 9本身对应的类是-1，因它本身大于2.5，所以被 G1(x) 分在了相应的类“-1”中，分对了。

　　从而得到 G1(x) 在训练数据集上的误差率（被 G1(x) 误分类样本“6、7、8”的权值之和） e1=P(G1(xi)≠yi)=3∗0.1=0.3 。 然后根据误差率 e1 计算 G1 的系数：

α1=12ln(1−e1e1)=0.4236

这个 α1 代表 G1(x) 在最终的分类函数中所占的权重为0.4236。
　　接着就是更新训练数据的权值分布，用于下一轮迭代:　　

Dm+1=(wm+1,1,wm+1,2,⋯,wm+1,i,⋯,wm+1,N)

wm+1,i=wmi/Zm⋅exp(−αmyiGm(xi)),   i=1,2,⋯,N

值得一提的是，由权值更新的公式可知，每个样本的新权值是变大还是变小，取决于它是被分错还是被分正确。即如果某个样本被分错了，则 yiGm(xi) 为负，负负得正，结果使得整个式子变大（样本权值变大），否则变小。

　　第一轮迭代后，最后得到各个数据新的权值分布

D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)

由此可以看出，因为样本中是数据“6、7、8”被 G1(x) 分错了，所以它们的权值由之前的0.1增大到0.1666，反之，其它数据皆被分正确，所以它们的权值皆由之前的0.1减小到0.0715。

　　分类函数 f1(x)=α1G1(x)=0.4236G1(x) 。此时得到的第一个基本分类器 sign(f1(x)) 在训练数据集上有3个误分类点（即6、7、8）。
　　从上述第一轮的整个迭代过程可以看出：被误分类样本的权值之和影响误差率，误差率影响基本分类器在最终分类器中所占的权重。

　　第二轮迭代：
　　对于 m=2 ，在权值分布为

D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)

的训练数据上，经过计算可得：
　　● 阈值 θ 取2.5时误差率为0.1666*3（x < 2.5时取1，x > 2.5时取-1，则6、7、8分错，误差率为0.1666*3）；
　　● 阈值 θ 取5.5时误差率最低为0.0715*4（x > 5.5时取1，x < 5.5时取-1，则0、1、2、9分错，误差率为0.0715*3 + 0.0715）；
　　● 阈值 θ 取8.5时误差率为0.0715*3（x < 8.5时取1，x > 8.5时取-1，则3、4、5分错，误差率为0.0715*3）。
　　所以阈值 θ 取8.5时误差率最低，故第二个基本分类器为：　　

G２(x)={1,       x<８.5−1,    x≥８.5

　面对的还是下述样本：　　

很明显， G2(x) 把样本“3、4、5”分错了，根据 D2 可知它们的权值为0.0715、0.0715、0.0715，所以 G2(x) 在训练数据集上的误差率 e2=P(G2(xi)≠yi)=3∗0.0715=0.2143 。 然后根据误差率 e2 计算 G2 的系数：　

α２=12ln(1−e２e２)=0.6496

　　更新训练数据的权值分布，用于下一轮迭代:

Dm+1=(wm+1,1,wm+1,2,⋯,wm+1,i,⋯,wm+1,N)

wm+1,i=wmi/Zm⋅exp(−αmyiGm(xi)),   i=1,2,⋯,N

由上述公式得到

D3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)

被分错的样本“3、4、5”的权值变大，其它被分对的样本的权值变小。
分类函数 f2(x)=α1G1(x)+α2G2(x)=0.4236G1(x)+0.6496G2(x) 。此时得到的第二个基本分类器 sign(f2(x)) 在训练数据集上有3个误分类点（即3、4、5）。

　　第三轮迭代：
　　对于 m=3 ，在权值分布为

D3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)

的训练数据上，经过计算可得：
　　● 阈值 θ 取2.5时误差率为0.1060*3（x < 2.5时取1，x > 2.5时取-1，则6、7、8分错，误差率为0.1060*3）；
　　● 阈值 θ 取5.5时误差率最低为0.0455*4（x > 5.5时取1，x < 5.5时取-1，则0、1、2、9分错，误差率为0.0455*3 + 0.0715）；
　　● 阈值 θ 取8.5时误差率为0.1667*3（x < 8.5时取1，x > 8.5时取-1，则3 4 5分错，误差率为0.1667*3）。
　　所以阈值 θ 取8.5时误差率最低，故第三个基本分类器为：

G3(x)={1,       x>5.5−1,    x≤5.5

　面对的还是下述样本：　

此时，被误分类的样本是：0、1、2、9，这4个样本所对应的权值皆为0.0455。所以 G3(x) 在训练数据集上的误差率 e3=P(G3(xi)≠yi)=4∗0.0455=0.1820 。 然后根据误差率 e3 计算 G3 的系数：

α3=12ln(1−e3e3)=0.7514

　　更新训练数据的权值分布，用于下一轮迭代:

Dm+1=(wm+1,1,wm+1,2,⋯,wm+1,i,⋯,wm+1,N)

wm+1,i=wmi/Zm⋅exp(−αmyiGm(xi)),   i=1,2,⋯,N

由上述公式得到

D4=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125)

被分错的样本“0、1、2、9”的权值变大，其它被分对的样本的权值变小。
分类函数 f3(x)=α1G1(x)+α2G2(x)+α3G3(x)=0.4236G1(x)+0.6496G2(x)+0.7514G3(x) 。此时得到的第三个基本分类器 sign(f3(x)) 在训练数据集上有0个误分类点。至此，整个训练过程结束！

迭代总结：
现在来总结下三轮迭代下来，各个样本权值和误差率的变化，如下所示（其中，样本权值D中用蓝色表示在上一轮中被分错的样本的新权值）：训练之前，各样本的权值被初始化为

D1=(0.1，0.1,0.1,0.1,0.1,0.1，0.1,0.1,0.1,0.1).

第1轮迭代， 样本“6、7、8”被分错，对应的误差率为 e1=P(G1(xi)≠yi)=3∗0.1=0.3 ，第一个基本分类器在最终的分类器中所占的权重为 α1=0.4236 。样本权值调整为：

D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715);

第2轮迭代， 样本“3、4、5”被分错，对应的误差率为 e2=P(G2(xi)≠yi)=3∗0.0715=0.2143 ，第二个基本分类器在最终的分类器中所占的权重为 α2=0.6496 。样本权值调整为：

D3=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455)；

第3轮迭代， 样本“0、1、2、9”被分错，对应的误差率为 e3=P(G3(xi)≠yi)=4∗0.0455=0.1820 ，第三个基本分类器在最终的分类器中所占的权重为 α3=0.7514 。样本权值调整为：

D4=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125).

从上述过程中可以发现，如果某些个样本被分错，它们在下一轮迭代中的权值将被增大，反之，其它被分对的样本在下一轮迭代中的权值将被减小。就这样，分错样本权值增大，分对样本权值变小，而在下一轮迭代中，总是选取让误差率最低的阈值来设计基本分类器，所以误差率 e （所有被 Gm(x) 误分类样本的权值之和）不断降低。
综上，将上面计算得到的 α1、α2、α3 各值代入 G(x) 中得到最终的分类器为：

G(x)=sign(f3(x))=sign(α1G1(x)+α2G2(x)+α3G3(x))=sign(0.4236G1(x)+0.6496G2(x)+0.7514G3(x))

测试代码

最后的输出结果是：

最后一张图显示第三个基本分类器 sign(f3(x)) 在训练数据集上没有误分类点。

[同步本人网易博客的文章]AdaBoost 人脸检测介绍(4) : AdaBoost算法举例