【技术点】数据结构--二叉树(一)
文章目录
- 前言
- 基本二叉树
- 二叉树定义
- 二叉树遍历
- 满二叉树 & 完全二叉树
- BST - 搜索二叉树
- 搜索
- 新增节点
- 删除
- 线索二叉树
- 霍夫曼树
- 霍夫曼树的构造方式
- 构造霍夫曼树伪代码
- 下一步
前言
二叉树,数据结构的终结者,面试官的最爱。
BST,红黑树,完全二叉树各种概念很容易就傻傻分不清楚。
以前了解的东西都很散,写个文章将这些东西记录清楚。
基本二叉树
二叉树定义
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是一个递归的概念。
二叉树遍历
- 深度优先搜索
- 广度优先搜索
应该说,树这种数据结构都是这两种搜索方式。
树的遍历可以认为是把树这种结构进行序列化的过程。
满二叉树 & 完全二叉树
满二叉树:二叉树中所有非叶子结点的度都是2,且叶子结点都在同一层次上
完全二叉树:如果一个二叉树与满二叉树前m个节点的结构相同,这样的二叉树被称为完全二叉树
也就是说,如果把满二叉树从右至左、从下往上删除一些节点,剩余的结构就构成完全二叉树
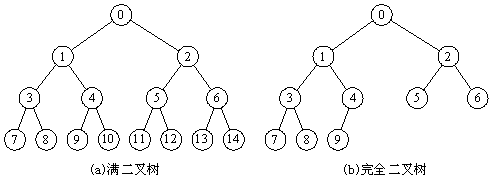
在满二叉树和完全二叉树完全可以用一维线性结构(数组)来存储。
用广度优先搜索来遍历图中(a)的满二叉树时,数组为:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ,13 ,14]。value=0的数组下标为1的话,他的左子树value=1的下标就为2,value=2的下表为3。更一般地:左子树下表与当前节点下表的关系为:2n,右子树为:2n+1
BST - 搜索二叉树
上述的二叉树在搜索性能上是不够好的,在搜索算法中,二分查找是一个很好的算法思路,而二叉树又正好是分成两部分,就是为二分查找量身定做的:这就是BST,搜索二叉树。
- BST的特点:每个节点的值大于其任意左侧子节点的值,小于其任意右节点的值。

任意一个节点,这个节点的键值大于它的左子树里的任何节点的键值,小于右子树里的任何节点的键值。
搜索
搜索时的算法就和二分查找一样(伪代码,主要是为了说明步骤,后面的代码也是):
function find(x, root)
{
if (x.value == root.value){
return root
}else if (x.value > root.value){
find(x, root.right)
}else {
find(x, root.left)
}
}
搜索起来HAPPY了,但是在树节点变动,也就是新增节点和删除节点时就需要维护树的结构了。
新增节点
function addNode(root, x){
if (root is null){ //root 为空
root = x
return root
}
x = find(x, root) //已有
if (x is not null){
return false
}
if (x.value < root.value){
if (root.left is null){
root.left = x
}else{
addNode(root.left, x)
}
}else{
if (root.rightis null){
root.right= x
}else{
addNode(root.right, x)
}
}
}
删除
删除比较复杂一点,要考虑三种场景。
节点为叶子节点
节点有一个节点
节点有两个节点
function del(root, x){
node, parent = find(root, x) //这里改造一下,找到节点的时候把parent也返回出来,没有单独写代码了
if (node is null){ //没有找到
return false
}
if (node.left is null & node.right is null){ //叶子节点
if(parent.value > node.value){ //node为左子树
parent.left = null //parent的左子树赋空
}else{
parent.right= null //parent的右子树赋空
}
}
if (node.left is null & node.right is not null){
if(parent.value > node.value){ //node为parent的左子树
parent.left = node.right //parent的左子树直接指向node的右子树,parent会比所有子树节点都大
}else{
parent.right = node.right //parent的左子树直接指向node的右子树,parent会比所有子树节点都小
}
}
if (node.left is not null & node.right is null){
if(parent.value > node.value){ //node为parent的左子树
parent.left = node.left //parent的左子树直接指向node的左子树,parent会比所有子树节点都大
}else{
parent.right = node.left //parent的左子树直接指向node的右子树,parent会比所有子树节点都小
}
}
//若该节点含有两个子节点,一般的删除策略是用其右子树的最小结点代替待删除结点的数据,然后递归删除那个右子树最小结点。
if (node.left is not null & node.right is not null){
minRight = getMinBst(node) //找到当前节点右子树下的最小节点,就是紧跟这个这个节点键值的节点
node.value = minRight.value
if(minRight == node.right){ //找到的恰好就是删除节点的右子树
parent.right = minRight.right
}
else
parent.left = minRight.right;
}
}
可以看出来,搜索是简单了,但是一旦树结构有变化的话,操作代价还是很大的,所以一般适用于大量搜索,一般不会有经常性结构变化的场景。
线索二叉树
在节点中加入这个节点的前驱和后驱,使得树形结构成为一个线性结构的树,就是线索二叉树。
在满二叉树和完全二叉树的情况下,是不需要专门的信息,如果不是的话,可以在每个节点中增加两个成员:prev和next。这样就便于二叉树按照某种规则做遍历。但是同样在树的结构变动时,会增加额外的操作成本。
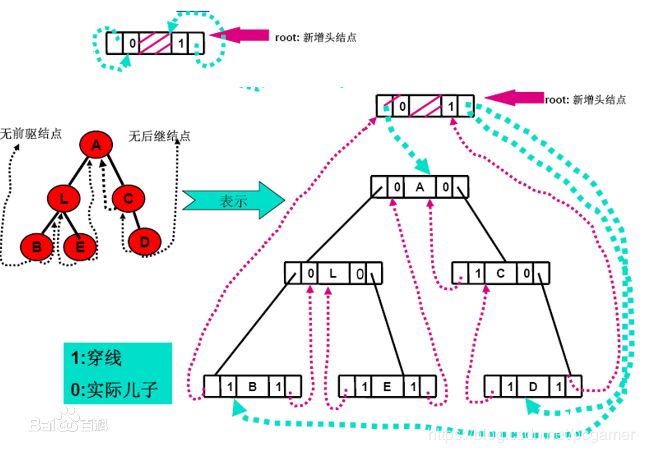
霍夫曼树
在计算机数据处理中,哈夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
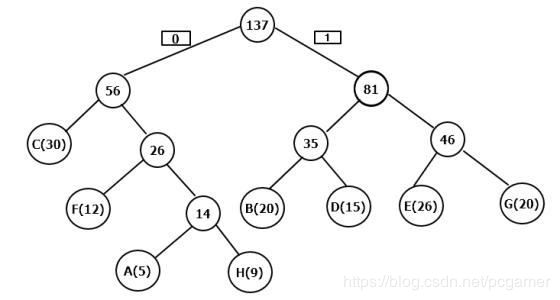
对C F A H B D E G进行编码,每个字母的编码权重为节点键值,左子树编码为0,右子树编码为1。
那么各字母的编码如下:
C:00
F:010
A:0110
H:0111
B:100
D:101
E:110
G:111
可以看出,基本上是权重高的编码就短。所以可以达到最佳的利用率。
因为只用到了叶子节点进行编码,所以不存在某个编码串是另一个编码串子串的问题。
霍夫曼树的构造方式
- 构造频率表,并按从小到大排序。比如上面提到的几个字母
A:5 H:9 F:12 D:15 G:20 B:20 E:26 C:30 - 挑出最前面两个,也就是A和H,小的作为左子树,大的作为右子树,根节点为两者频率之和。并把这个和加入频率表
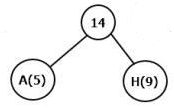
频率表成为:
F:12 第一步的和:14 D:15 G:20 B:20 E:26 C:30 - 重复第二步,挑出的是F和第一步的和。
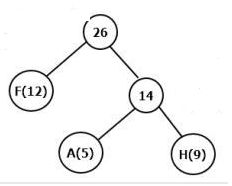
频率表成为:D:15 G:20 B:20 第三步的和: 26 E:26 C:30 - 后面依次类推。
构造霍夫曼树伪代码
type element{
key,
weight
}
function createHuffmanTree(element e[]){
sorted_E = sort(e) //用任何排序算法
while(sorted_E.count() > 2){
root = new node(sorted_E[0].weight + sorted_E[1].weight) //前两个数的权重相加作为两者的根节点
new_ele = new element(0, sorted_E[0].weight + sorted_E[1].weight) //用于更新频率数组
if (sorted_E[0].weight < sorted_E[1].weight){
root.left = sorted_E[0].weight
root.right = sorted_E[1].weight
}else{
root.left = sorted_E[1].weight
root.right = sorted_E[0].weight
}
sorted_E.remove(sorted_E[0])
sorted_E.remove(sorted_E[1])
sorted_E.add(new_ele)
}
return root
}
下一步
未完待续,还有平衡二叉树,红黑树,B树,B+树等内容。