【2017CS231n】第七讲：训练神经网络（下）

先回顾一下第六讲：

    数据预处理。
    当我们对数据进行归一化红，分类器对权重矩阵的扰动不是特别敏感，鲁棒性更好。左边的分类器稍微变动一点就会破坏分类效果。

    右边的数据移到原点附近，并缩小单位方差，仍然可以进行良好的分类。当我们稍微转动分类的直线，损失函数对参数中的变动就不那么敏感，从而让优化变得容易。

1. 更好的优化

1.1 随机梯度下降法

训练神经网络的核心策略是一个优化问题。写下损失函数，定义权重的值。损失函数告诉我们权重值是好是坏。

    在上图的例子中我们只优化w1和w2，来找到蓝色区域，对应损失最小的权重值。

    上例中的随机梯度下降算法，我们首先评估一小批数据中损失的梯度，接下来向梯度为负的方向更新向量，它给出了损失函数下降最快的方向。

    但是存在一个问题，损失函数下降在w1方向上变化不敏感，在w2方向上变化比较敏感。

1.2 随机梯度下降存在的问题

1.2.1 之字形

    

    上面的两个球看做两个参数w1和w2，损失函数在w1也就是x轴方向变化不敏感，在y轴变化很敏感。

    在这类函数中运行随机梯度下降，会得到之字形图案。

    这类函数的最小值跟梯度并不是在一条直线上，当计算梯度并沿着梯度前进，会一遍一遍跨越等高线，之字形前进或后退。导致在水平维度上前进速度很慢，在非常敏感的垂直维度上做之字形运动。

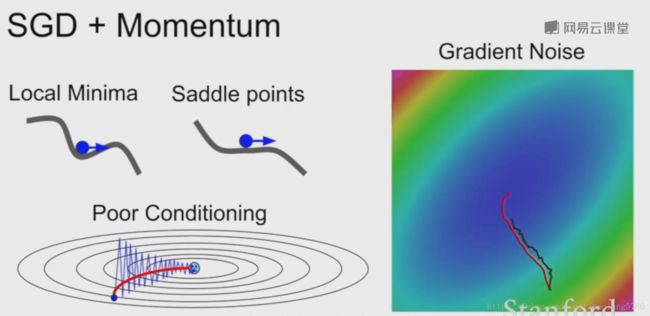
1.2.2 局部极小值

    图中的两条曲线。x轴代表一个参数，y轴代表损失函数值。
    在上面那条曲线中，我们遇到了鞍点。因为在sgd（随机梯度下降）中我们计算梯度，沿着梯度负方向前进，但是此时梯度为0，停止前进，我们就停留在了局部最小值。
    下面那条曲线，最小值点并不是在鞍点上，但是在鞍点附近，这个位置斜率非常小，此时我们前进会非常缓慢。

1.3 解决随机梯度下降存在的问题的方法

1.3.1 带动量的SGD

    如上面所示，左边是传统的SGD，右边是带动量的SGD。

    带动量SGD思想：保持一个不随时间变化的速度，将梯度估计添加到这个速度上，然后在这个速度方向上步进，而不是在梯度方向上步进。

    摩擦系数p对速度进行衰减，通常取0.9。我们用当前速度乘以摩擦系数p， 对速度进行衰减后加到梯度上，我们在速度向量的方向前进。

    带动量的SGD解决了我们之前讨论的问题。
    可以想象成一个球滚落下山，下落时速度会变快，当通过局部极小值点时，即使梯度为零，但是这个点仍有速度，我们就会越过局部极小值点继续下降。

    红色是带有动量的SGD。该方法对解决之字形前进也有用。

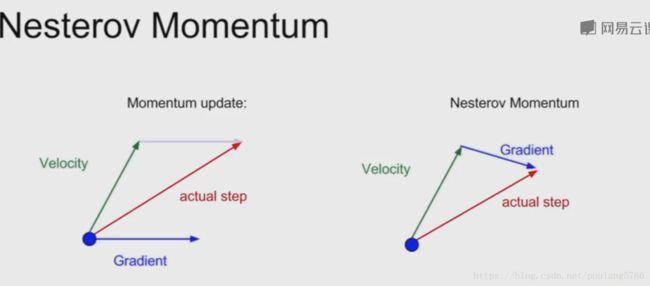
    左边的图是带动量SGD：蓝色是当前梯度方向，绿色是速度方向，我们的前进方向是这两者的平均权重，这有助于克服梯度方向上的噪声。估算梯度，然后取速度方向和梯度的混合作为当前前进方向
    右边的图是Nesterov加速梯度，也叫Nesterov加速动量。
从蓝点开始，在取得速度的方向上进行步进，之后评估这个位置的梯度，然后回到初始位置将这两者混合。

    将Nesterov用换元法改写一下，balala（看推倒吧）就可以同时计算损失函数和梯度。

1.3.2 AdaGrad算法

    下面说一下AdaGrad算法。

    在优化过程中需要保持一个在优化过程中每一步的梯度的平方和的持续估计，与速度项不同，现在我们有了梯度平方项，在训练时我们会一直累加当前梯度的平方到这个梯度平方项。当更新参数向量时，我们会除以这个梯度平方项。

    理解：我们有两个坐标轴，沿着一个轴我们有很高的梯度，另一个轴梯度很小，随着累加小梯度的平方，我们会在最后更新参数向量时除以一个很小的数字从而加速了这个方向的梯度；另一个轴由于梯度很大，我们会除以一个较大的数字从而降低这个维度的训练速度。

    随着时间的增长，步长会发生什么变化呢？

    随着时间的增长我们的步长会变得越来越小，因为我们一直随时间累加梯度的平方估计值，所以估计值越来越大我们的步长越来越小。
    学习目标是凸函数时这个特性会非常好，因为在越接近极值点时我们步长越小，我们会逐渐慢下来最后收敛。
但是非凸函数会让你困在局部极值点，使得训练过程无法继续。

1.3.3 RMSProp（对AdaGrad的改进）    

    由于AdaGrad在非凸函数中存在的缺陷，提出了RMSProp。

    改进后我们不是仅仅累计梯度平方，而是梯度平方按照一定比率下降。

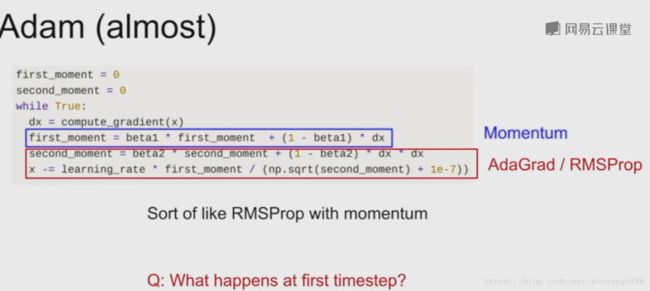
1.3.4 Adam算法

    将带动量SGD和RMSProp结合。

    我们更新第一动量和第二动量的估计值。

    蓝框中第一动量估计值等于梯度的加权和，第二动量的动态估计，就像AdaGrad和RMSProp算法，是一个梯度平方的动态近似。

    更新时，我们用第一动量除以第二动量的平方根。
    但是在第一步时会遇到问题：我们把第二动量设置为0，衰减率0.9，两者相乘还是接近于0。第一动量除以第二动量的值就会非常大， 也就是我们的第一步会非常大。
    注意：1e-7为了保证我们不是除以0。
    加了偏置矫正项，来避免刚开始步长过大。
    构造了第一和第二动量后，又构造了他俩的无偏估计。现在实际上我们使用无偏估计来做每一步更新，而不是初始的第一第二动量估计值。

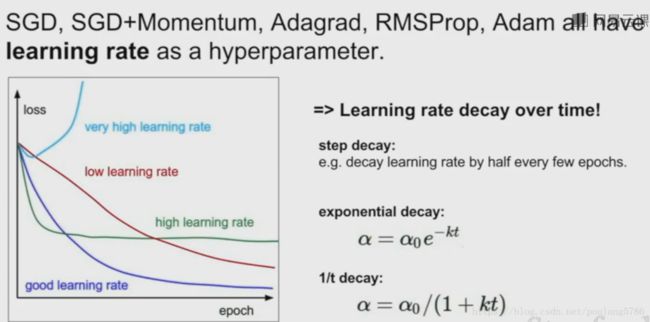
1.4 学习率

    可以设置学习率随时间衰减。刚开始较大，后来较小。
    步长衰减：例如第10万次迭代时衰减一个因子。

    指数衰减：训练时持续衰减。

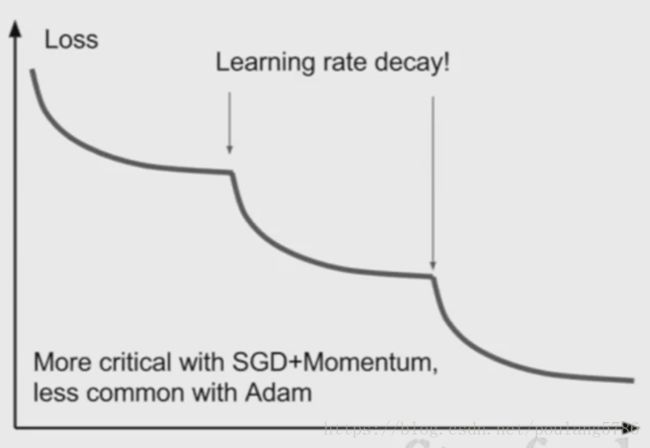
    这个损失函数的曲线是采用步长衰减学习率时的曲线。
    降低学习率可以降低损失的原因：假设模型此时取得了一个不错的取值区域，但是此时梯度已经很小了，保持原先的学习率只能在最优点附近来回徘徊。但如果我们降低了学习率，损失仍能继续降低。
    带动量的SGD更常用学习率衰减，Adam不常用。
    刚开始不要用学习率衰减，然后观察损失曲线，看看应该在什么地方使用学习率衰减。

1.5 二阶优化

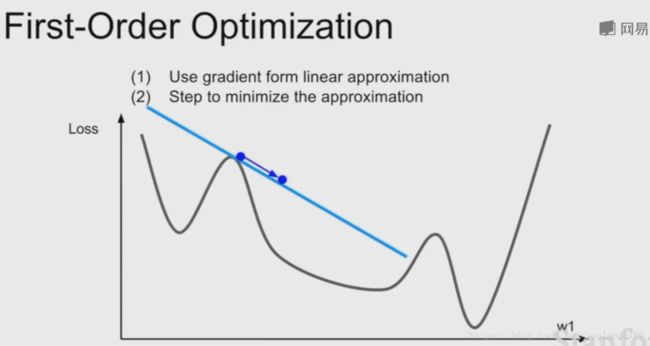
    在一阶优化中，我们求该点梯度，用梯度信息来求这个函数的线性逼近，相当于对函数进行一阶泰勒逼近。假设这个逼近就是该函数，但是该逼近只在很小的一个区间上成立，所以我们想迈出一步寻找极小值时不能迈出太大的一步。

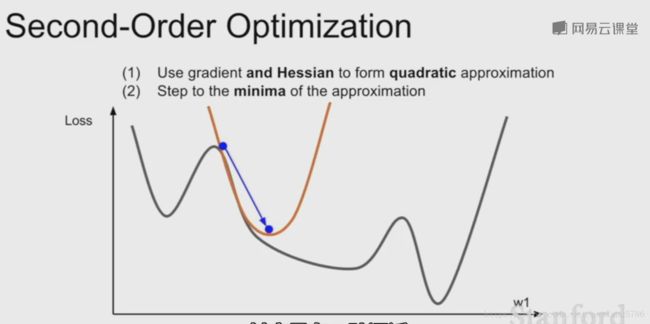
    对函数用了一个二阶泰勒逼近，它可以直接迈到最小值。

    把它拓展到多维，就是牛顿步长。计算海森矩阵即这个二阶偏导矩阵，接着求海森矩阵的逆，以便直接走到对函数二次逼近后的最小值的地方。

    在这里我们没有用到学习率，只是每次直接走到最小值点。

    但是直接求海森矩阵的逆计算量太大，所以我们的做法是去逼近这个矩阵的逆。这就引出了下面的方法，拟牛顿法（L-BFGS）。

    这些二阶逼近不太常用于随机情况的处理，而且在非凸问题上表现不是很好，

1.6 在实际中使用的优化

    实际中Adam已经适用于大多数情况。但是如果能够承受很多批次的更新而且没有很多随机情况需要处理，L-BFGS可以使用。（风格迁移中，随机性很少，参数也很少，适用）。

1.6.1 模型集成

    

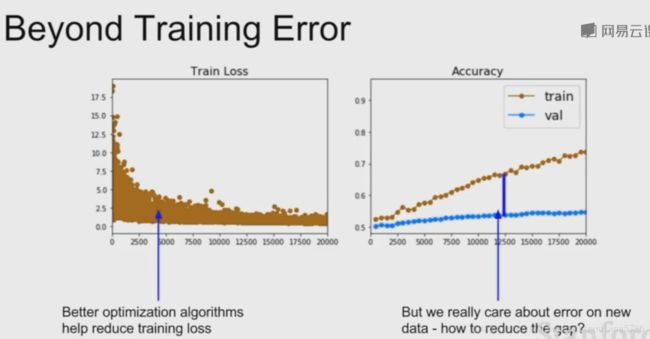
    在实际中我们更在意测试集上的误差和训练集与测试集之间的差距。

    模型集成：我们选择从不同的随机初始值上训练10个不同的模型，测试时我们在10个不同的模型上运行测试数据，然后平均10个模型的预测结果。把这10个模型加在一起可以缓解一点过拟合，从而提高一些性能。（在比赛时常用）

    可以在训练时保留多个模型的快照，用这些模型做集成。测试阶段仍需要把这些快照的预测结果做平均。

1.6.2 Polyak平均

    Polyak平均：在训练模型的时候，对不同时刻每个模型参数求指数衰减平均值，从而得到网络训练中一个比较平滑的集成模型，只后用这些平滑衰减的模型参数，而不是截止在某一时刻的模型参数。

2. 正则化

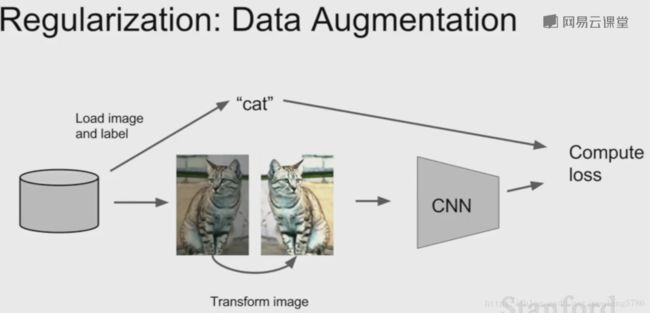
    正则化有利于提升网络的鲁棒性，避免过拟合。正则化主要有以下几种方法。

2.1数据增强

    随机转换一些图片（旋转平移等），标签不变。

    还可以对图像进行反转，缩放，裁剪，还可以采用色彩抖动，如改变亮度和对比度。

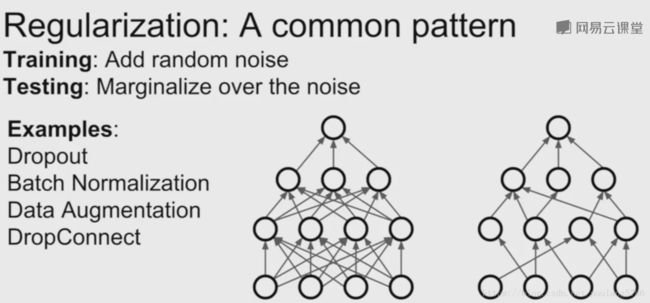
2.2 Dropconnect

    Dropconnect随机将权重矩阵中的一些元素置零。

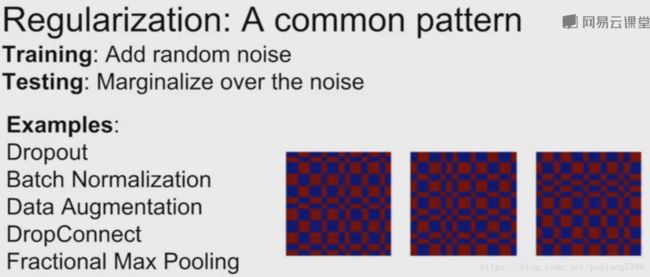
2.3 部分最大池化

    以前在固定区域池化，现在随机选择池化区域。测试时为了抵消随机性，可采用固定区域或平均。

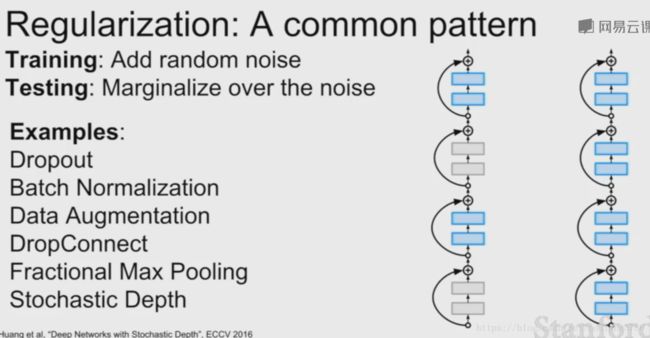
2.4 随机深度

    我们有一个很深的网络，但是在训练时丢弃部分层，测试时使用全部层。

3. 迁移学习

    1.先找到一些卷积神经网络，例如VGG，首先用该网络在一个非常大的数据集上训练，此时有足够的训练数据。
    2.（当你只有很少的数据时）把从这个训练集训练出来的提取特征的能力，用到你感兴趣的小的数据集上。此时我们只有C个分类。所以首先修改从最后一层的特征到最后的输出分类之间的全连接层，重新初始化最后的矩阵。现在只需要训练一个线性分类器，只需要训练最后这层让它在你的数据上收敛。
    3.（当你有稍微多一些的数据）可以微调整个网络让它在最后一层收敛。
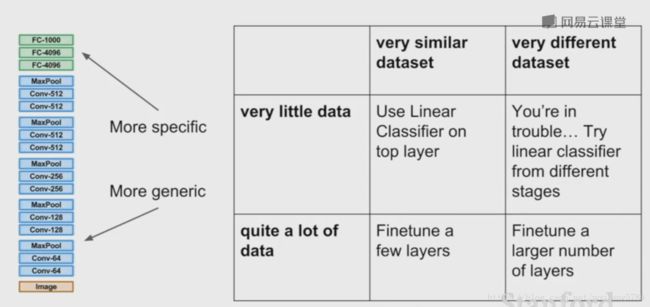
    大致的策略是，你拥有的数据越多，调整这个网络的部分就越多。

    更新网络的策略：调低学习率，比如最初的网络在ImagNet上收敛，此时的网络泛化能力已经很强了，我们希望微调网络使他适应我们的数据，所以应该降低学习率。

    如果我们的数据跟ImagNet上的很相似，我们只需要训练最后的线性分类器，数据多一些可以调整更多的部分。
    如果数据不相同，例如X光或CT图像，这时就需要调整大部分网络。