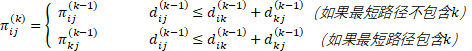[算法导论笔记]--所有结点对的最短路径问题
本文所贴示的伪代码均来源《算法导论》,本文只是对其中《所有结点对的最短路径问题》章节的简单总结,许多数学证明过程已忽略。
对于给定有向图G=(V,E)理论上,我们可以使用|V|次单源最短路径算法来解决所有结点对之间的最短路径问。但除此之外,我们可以利用动态规划来解决此问题(因为一条最短路径的子结构也包含了最短路径).
一、基础解法
最短路径的结构:
对于有向图G=(V,E)的所有结点对的最短路径问题,可以证明一条最短路径的所有子路径都是最短路径。假定用邻接矩阵来表示输入图,即W=( ![]() ). 考虑从结点i到结点j的一条最短路径p,假定p至多包含m条边,还假定没有权重为负值的环路,且m为有限值。
). 考虑从结点i到结点j的一条最短路径p,假定p至多包含m条边,还假定没有权重为负值的环路,且m为有限值。
如果i=j,则p的权重为0且不包含任何边。如果结点i和j不同,则可以将其分解为i~k->j,其中路径i~k(用p’表示)至多包含m-1条边。可以证明,p’是从结点i到k的一条最短路径。因此,δ(i,j)=δ(i,k)+ ![]() 。
。
对所有结点对最短路径问题的递归解
现在假设)![]() 为从结点i到结点j至多包含m条路边的任意路径中的最小权重。当m=0时,从结点i到j之间存在一条没有边的路径当且仅当i=j。因此有
为从结点i到结点j至多包含m条路边的任意路径中的最小权重。当m=0时,从结点i到j之间存在一条没有边的路径当且仅当i=j。因此有
对于m>=1,我们需要计算的![]() 是
是![]() 的最小值和从i到j最多由m条边组成的任意路径的最小权重。我们通过对j的所有可能前驱k进行检查来获得该值,因此递归定义:
的最小值和从i到j最多由m条边组成的任意路径的最小权重。我们通过对j的所有可能前驱k进行检查来获得该值,因此递归定义:
![]()
因为对于所有的j有 ![]() ,所以上述等式后面的式子成立。
,所以上述等式后面的式子成立。
但是真正的最短路径权重δ(i,j)是多少呢?如果图G不包含权重为负值的环路,则对于每一结点i和j,如果δ(i,j)<∞,从i到j之间存在一条最短路径。由于该路径是简单路径,最多包含n-1条边,从结点i到结点j由多于n-1条边构成的路径不可能比前者更短。因此,真正的最短路径权重可以由下面公式得出:
![]()
自底向上计算最短路径
根据输入矩阵W=( ![]() ),现在可以计算出矩阵序列
),现在可以计算出矩阵序列![]() 、
、![]() 、…
、…![]() ,其中对于m=1,2…n-1有
,其中对于m=1,2…n-1有![]() =
= ![]() ,最后的矩阵
,最后的矩阵![]() 包含的是最短路径的实际权重。注意,对于所有的结点i和j,
包含的是最短路径的实际权重。注意,对于所有的结点i和j,![]() = (
= ( ![]() ) , 因此
) , 因此 ![]() 。
。
算法的核心伪代码如下:
二、Floyd-Warshall算法
在Floyd算法中,对一条最短路径的描述和上文稍有不同。Floyd算法考虑的是一条最短路径的中间结点。这里,简单路径p=
Floyd算法依赖于下面的观察,假定图G的所有结点为V={1,2…n};考虑到其中的一个子集{1,2…k},这里k是某个小于n的整数,并且设p为其中权重最小的路径(路径p是简单路径)。Floyd算法利用了路径p和从i到j之间中间结点均取自集合{1,2,…k-1}的最短路径之间的关系。该关系依赖于结点k是否是路径p上的一个中间结点。
·如果结点k不是路径p上的中间结点,则路径p上的所有中间结点一定属于集合{1,2…k-1};所以从结点i到j的中间结点取自{1,2…k}的最短路径也是结点i到j的中间结点取自{1,2…k-1}的最短路径;
·如果结点k是路径p上的中间结点,则路径p可以表示为i~k~j;其中i~k为路径p1,k~j为路径p2.显然,路径p1上的所有中间结点必定在{1,2…k-1}中,自然,p1是从结点i到k的中间结点位于{1,2…k-1}的最短路径。对于p2实际上也是同理,很容易退出,p2也是从结点k到j上的中间结点位于{1,2,…k-1}的一条最短路径;
于是,我们可以得到此问题的递归解:
其中![]() 表示从i到j的中间结点都属于集合{1,2…k}的一条最短路径的权重。
表示从i到j的中间结点都属于集合{1,2…k}的一条最短路径的权重。
由此,可以很容易得到Floyd算法的伪代码(自底向上的DP方法)
构建一条最短路径
在Floyd算法中,可以有许多不同的方法来构建最短路径,一种办法是先计算最短路径的权重矩阵D,然后用D来构造前驱矩阵Π。
另外,我们可以计算矩阵![]() 的同时计算前驱矩阵Π。具体来说,我们将计算一个矩阵序列
的同时计算前驱矩阵Π。具体来说,我们将计算一个矩阵序列![]() 、
、![]() 、…
、…![]() ,并且定义
,并且定义 ![]() 为从节点i到k的一条所有中间结点都取自集合{1,2…k}的最短路径上的j的前驱结点。
为从节点i到k的一条所有中间结点都取自集合{1,2…k}的最短路径上的j的前驱结点。
这里可以推出![]() 的一个递推式,当k=0时,从i到j的一条最短路径没有中间结点,因此
的一个递推式,当k=0时,从i到j的一条最短路径没有中间结点,因此
对于k>=1,如果考虑路径i~k~j,这里k != j,则所选择的结点j的前驱与我们选择的从结点k到j的一条中间结点全部取自集合{1,2…k-1}的最短路径上的前驱相同。如果不含中间结点的话,所选择的结点j的前驱和所选择的从结点i到j的一条中间结点全部出自集合{1,2…k-1}的最短路径的前驱是一样的。因此有:
这里,只要把矩阵Π带入到Floyd算法流程中,与矩阵D一同计算即可。
![[算法导论笔记]--所有结点对的最短路径问题_第1张图片](http://img.e-com-net.com/image/info8/28c969c5e93742718040298576610864.jpg)
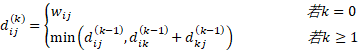
![[算法导论笔记]--所有结点对的最短路径问题_第2张图片](http://img.e-com-net.com/image/info8/404d4d3ee2614f25bce8d4efe3b08843.jpg)