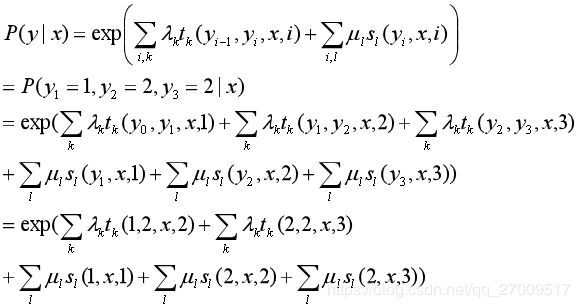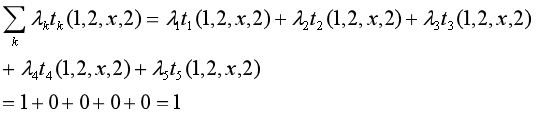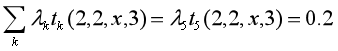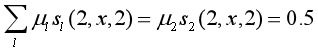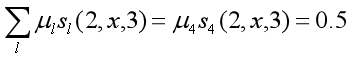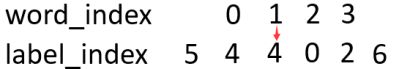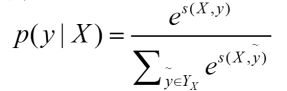条件随机场的理论和例子--(2)
文章目录
- 3.条件随机场
- 4.线性链条件随机场
- 4.1.线性链条件随机场的参数化形式
- 4.2.条件随机场的简化形式
- 4.3.条件随机场的矩阵形式
- 5.条件随机场与HMM的区别
- 6.NER的例子
- 6.1.计算过程
3.条件随机场
随机场:随机场是一种图模型,包含结点的集合和边的集合,结点表示一个随机变量,而边表示随机变量之间的依赖关系。如果按照某一种分布随机给图中每一个结点赋予一个值,则称为随机场。
马尔科夫随机场:马尔科夫性质指某一个时刻t的输出值只和t-1时刻的输出有关系,和更早的输出没有关系。马尔科夫随机场则是一种特殊的随机场,其假设每一个结点的取值只和相邻的结点有关系,和不相邻结点无关。
条件随机场(conditional random field,CRF):CRF 是一种特殊的马尔科夫随机场,CRF 假设模型中只有 X (观测值) 和 Y (状态值)。在 CRF 中每一个状态值 yi 只和其相邻的状态值有关,而观测值 x 不具有马尔科夫性质。注意观测序列 X 是作为一个整体影响 Y 计算,如下图所示。

线性链条件随机场 Linear-chain CRF:线性链条件随机场指序列 Y 和 X 都是线性链的条件随机场,如下图所示。
条件随机场可以用于不同的预测问题,主要讲述线性链(linear chain)条件随机场,这时,问题变成了由输入序列对输出序列预测的判别模型,形式为对数线性模型,其学习方法通常是极大似然估计或正则化的极大似然估计。
条件随机场的定义:
设X与Y是随机变量,P(Y|X)是在给定X的条件下Y的条件概率分布。若随机变量Y构成一个由无向图G=(V,E)表示的马尔科夫随机场,即:
![]()
对任意结点v成立,则称条件概率分布P(Y|X)为条件随机场,式中w~v表示在图G=(V,E)中与结点v有边连接的所有结点w,wv表示结点v以外的所有结点, Y v Y_v Yv, Y u Y_u Yu与 Y w Y_w Yw为结点v,u与w对应的随机变量。
CRF 条件随机场算法通常用于序列标注的任务,例如给定一个输入序列 X= (x1, x2, x3, …, xn),求输出的序列 Y = (y1, y2, y3, …, yn)。例如在中文分词中,X 即是输入的句子,Y 是句子中每一个单词对应的分词中的目标 (s, b, m, e)。因此 CRF 通常用于 NLP 的分词、词性标注、命名实体识别等任务。
X:X = (x1, x2, x3, …, xn) 表示输入的序列,也称为观测值,例如句子中所有单词。Y:Y = (y1, y2, y3, …, yn) 表示输出的序列,也称为状态值,例如句子中每一个单词的词性。
4.线性链条件随机场
线性链条件随机场的定义:
设 X = ( X 1 , X 2 , . . . , X N ) X=(X_1,X_2,...,X_N) X=(X1,X2,...,XN), Y = ( Y 1 , Y 2 , . . . , Y N ) Y=(Y_1,Y_2,...,Y_N) Y=(Y1,Y2,...,YN)均为线性链表示的随机变量序列,若在给定随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔科夫性:
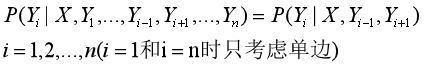
则称P(Y|X)为线性链条件随机场,在标注问题中,X表示输入观测序列,Y表示对应的输出标记序列或状态序列。
这里定义只讲线性链随机场,针对自然语言处理领域的处理进行设计,因此这里只提线性链随机场定义:
设 X = ( X 1 , X 2 , . . . , X n ) X=(X_1,X_2,...,X_n) X=(X1,X2,...,Xn), Y = ( Y 1 , Y 2 , . . . , Y n ) Y=(Y_1,Y_2,...,Y_n) Y=(Y1,Y2,...,Yn)均为线性链表示的随机变量序列,若在给定随机变量序列的条件下,随机变量序列Y的条件概率分布就构成条件随机场,即满足马尔科夫性:
![]()
则称P(Y|X)为线性链条件随机场。
在标注问题中,X表示输入观测序列,即句子,Y表示对应的输出标记序列或状态序列,即每个字的类别。

上面的团有X, Y 1 Y_1 Y1, Y 2 Y_2 Y2,其他的Y都不是这个团的,对应的条件概率,以 Y 2 Y_2 Y2为例,如下:
![]()
可以看出,的概率取决于输入序列X和,,体现了概率图模型里面的思想(符合语言的规律,联系上下文语意),不和其直接相连的可以看做条件独立,这就解释了下面为什么可以直接相乘,指数相加了。
4.1.线性链条件随机场的参数化形式
线性链条件随机场的参数化形式的定义:
设P(Y|X)为线性链条件随机场,则在随机变量X取值为x的条件下,随机变量Y取值为y的条件概率有如下形式:
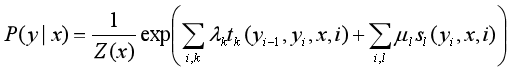
其中,
i:要标记序列的个数
k:特征函数的个数
t k t_k tk, s l s_l sl:特征函数
λ k \lambda_k λk, μ l \mu_l μl:对应的权重
Z(x):规范化因子
求和:在所有可能的输出序列上进行
t k t_k tk:定义在边上的特征函数,称为转移特征,依赖于当前位置和前一个位置
s l s_l sl:定义在结点上的特征函数,称为状态特征,依赖于当前位置
t k t_k tk和 s l s_l sl都依赖于位置,是局部特征函数,取值为0或1,满足特征条件时取值为1,否知为0.
所以,线性链条件随机场也是对数线性模型(log linear model)
例子:
设有一标注问题:
输入观测序列: X = ( X 1 , X 2 , X 3 ) X=(X_1,X_2,X_3) X=(X1,X2,X3),输出序列: Y = ( Y 1 , Y 2 , Y 3 ) , Y ∈ { 1 , 2 } Y=(Y_1,Y_2,Y_3),Y\in \{1,2\} Y=(Y1,Y2,Y3),Y∈{1,2}
假设特征 t k t_k tk和 s l s_l sl,对应的权重 λ k \lambda_k λk, μ l \mu_l μl如下:
![]()
即:
满足条件取值为1,否知为0.
对给定观测序列x,求标记序列为 y = ( y 1 , y 2 , y 3 ) y=(y_1,y_2,y_3) y=(y1,y2,y3)的非规范条件概率(即没有除以规范化因子的条件概率)
解:
4.2.条件随机场的简化形式
以特征为主要线索,每个特征的所有观测状态相加。
条件随机场还可以由简化形式表示。

该公式中的特征在各个位置都有定义,可以对同一个特征在各个位置求和,然后将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场简化为权重向量和特征向量的内积形式。
设有K1个转移特征,K2个状态特征,K=K1+K2,即:
然后对转移与状态特征在各个位置i求和,即:
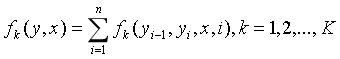
n:观测状态的个数。
用 w k w_k wk表示特征 f k ( y , x ) f_k(y,x) fk(y,x)的权重,即:
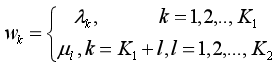
于是公式
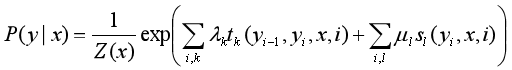
转为:

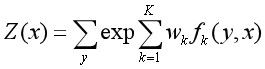
k:转移特征和状态特征的个数。
若w表示权重向量,即:
![]()
以F(y,x)表示全局特征向量,即:
![]()
则条件随机场可以写成向量w和F(y,x)的内积形式:
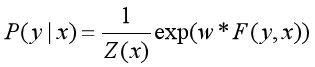
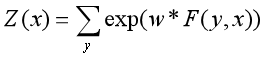
4.3.条件随机场的矩阵形式
以观测序列为线索。每个状态的所有特征相加。
对给定的观测序列x,相应的标记序列y,加上起点和终点标记, y 0 = s t a r t y_0=start y0=start, y n + 1 = s t o p y_{n+1}=stop yn+1=stop。
条件随机场的公式:
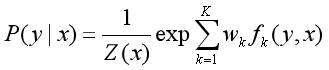
对观测序列x的每个位置i=1,2,…,n+1,定义一个m阶矩阵,m是标记y的个数,即:
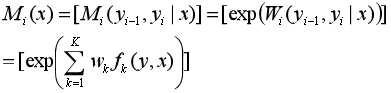
![]()

k:转移特征和观测特征的个数总和。
这样,给定观测序列x,标记序列y的非规范化概率可以通过n+1个矩阵的乘积 ∏ i = 1 n + 1 \prod_{i=1}^{n+1} ∏i=1n+1表示,于是,条件概率 P w ( y ∣ x ) P_w(y|x) Pw(y∣x)改为:
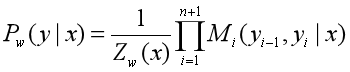
![]()
假设 y i ∈ { 1 , 2 , 3 } y_i \in \{1,2,3\} yi∈{1,2,3},即y只有三种状态可以选择,那么在某个时刻(观测状态)下, y i − 1 → y i y_{i-1} \rightarrow y_i yi−1→yi对应的转移矩阵如下:

例子:
下图是一个线性链条件随机场,观测序列x,状态序列y,i=1,2,3,n=3,标记 y i ∈ { 1 , 2 } y_i \in \{1,2\} yi∈{1,2},假设 y 0 = s t a r t = 1 y_0=start=1 y0=start=1, y 4 = s t o p = 1 y_4=stop=1 y4=stop=1,各个观测位置之间的随机矩阵 M 1 ( x ) M_1(x) M1(x), M 2 ( x ) M_2(x) M2(x), M 3 ( x ) M_3(x) M3(x), M 4 ( x ) M_4(x) M4(x)分别是:
![]()

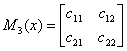
![]()
求状态序列y以start为起点stop为终点所有路径的非规范化概率及规范化因子。
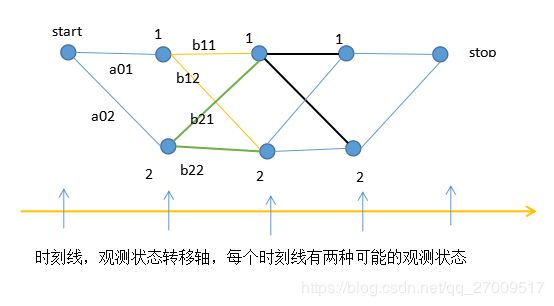
计算start到stop对应的y=(1,1,1),y=(1,1,2),y=(1,2,1),y=(1,2,2),y=(2,1,1),y=(2,1,2),y=(2,2,1),y=(2,2,2)的概率:
![]()
计算矩阵乘积 M 1 ( x ) M_1(x) M1(x) M 2 ( x ) M_2(x) M2(x) M 3 ( x ) M_3(x) M3(x) M 4 ( x ) M_4(x) M4(x),可得第一行第一列元素为:
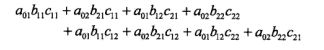
恰好等于从start到stop的所有路径的非规范化概率之和,即规范化因子Z(x)。
5.条件随机场与HMM的区别
对于词性标注问题,HMM模型也可以解决。HMM的思路是用生成办法,就是说,在已知要标注的句子s的情况下,去判断生成标注序列y的概率,如下所示:
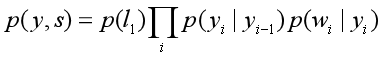
p ( y i ∣ y i − 1 ) p(y_i|y_{i-1}) p(yi∣yi−1)是转移概率,比如, y i − 1 y_{i-1} yi−1是介词, y i y_i yi是名词,此时的p表示介词后面的词是名词的概率。
p ( w i ∣ y i ) p(w_i|y_i) p(wi∣yi)表示发射概率(emission probability),比如 y i y_i yi是名词, w i w_i wi是单词“ball”,此时的p表示在是名词的状态下,是单词“ball”的概率。
CRF比HMM要强大的多,它可以解决所有HMM能够解决的问题,并且还可以解决许多HMM解决不了的问题。事实上,我们可以对上面的HMM模型取对数,就变成下面这样:

CRF的式子(简化):

不难发现,如果我们把第一个HMM式子中的log形式的概率看做是第二个CRF式子中的特征函数的权重的话,我们会发现,CRF和HMM具有相同的形式,只不过CRF可以有不同的特征。
用一句话来说明HMM和CRF的关系就是这样:
每一个HMM模型都等价于某个CRF
但是,CRF要比HMM更加强大,原因主要有两点:
-
CRF可以定义数量更多,种类更丰富的特征函数。HMM模型具有天然具有局部性,就是说,在HMM模型中,当前的单词只依赖于当前的标签,当前的标签只依赖于前一个标签。这样的局部性限制了HMM只能定义相应类型的特征函数,我们在上面也看到了。但是CRF却可以着眼于整个句子s定义更具有全局性的特征函数。 -
CRF可以使用任意的权重。将对数HMM模型看做CRF时,特征函数的权重由于是log形式的概率,所以都是小于等于0的。但在CRF中,每个特征函数的权重可以是任意值,没有这些限制。
6.NER的例子
这里的label_alphabet中的b代表一个实体的开始,即begin;m代表一个实体的中部,即mid;e代表一个实体的结尾,即end;o代表不是实体,即None;和分表代表这个标注label序列的开始和结束,类似于机器翻译的和。

这个就是word和label数字化后变成word_index,label_index。最终就变成下面的形式:

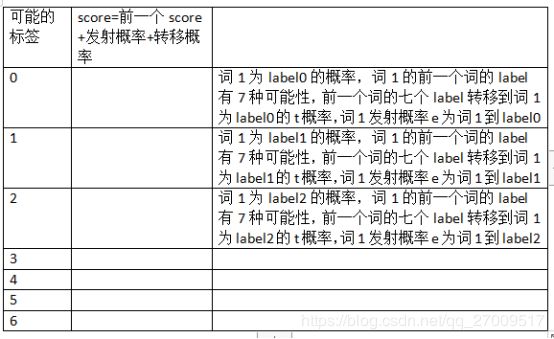
因为label有7种,每一个字被预测的label就有7种可能,为了数字化这些可能,我们从word_index到label_index设置一种分数,叫做发射分数emit:
看这个图,有word_index 的 1 -> 到label_index 的 4的小红箭头,像不像发射过来的?。
另外,我们想想,如果单单就这个发射分数来评价,太过于单一了,因为这个是一个序列,比如前面的label为o,那此时的label被预测的肯定不能是m或s,所以这个时候就需要一个分数代表前一个label到此时label的分数,我们叫这个为转移分数,即T:
如图,横向的label到label箭头,就是由一个label到另一个label转移的意思,此时的分数为T[4][4]。
此时我们得出此时的word_index=1到label_index=4的分数为emit[1][4]+T[4][4]。但是,CRF为了全局考虑,将前一个的分数也累加到当前分数上,这样更能表达出已经预测的序列的整体分数,最终的得分score为:
score[1][4] = score[0][4]+emit[1][4]+T[4][4]
所以整体的score就为:
![]()
下标为word_index和label_index
其中X为word_index序列,y为预测的label_index序列。
因为这个预测序列有很多种,种类为label的排列组合大小。其中只有一种组合是对的,我们只想通过神经网络训练使得对的score的比重在总体的所有score的越大越好。而这个时候我们一般softmax化,即:
其中分子中的s为label序列为正确序列的score,分母s为每种可能的score。
这个比值越大,我们的预测就越准,所以,这个公式也就可以当做我们的loss,可是loss一般都越小越好,那我们就对这个加个负号即可,但是这个最终结果手机趋近于1的,我们实验的结果是趋近于0的,这时候log就派上用场了,即:
6.1.计算过程
就是为了求得所有预测序列可能的得分和。我们第一种想法就是每一种可能都求出来,然后累加即可。可是,比如word长为10,那么总共需要计算累加10^7次,这样的计算太耗时间了。那么怎么计算的时间快呢?这里有一种方法:

s:score[][]:word_index,label_index
t:label2label
e:word2label
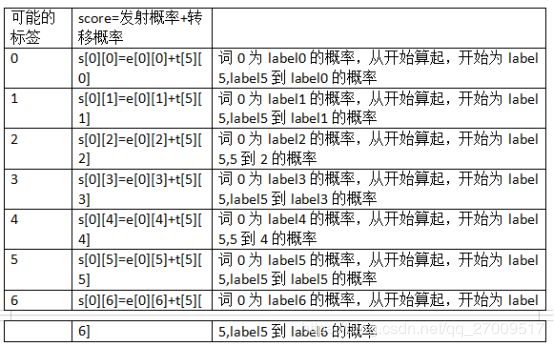
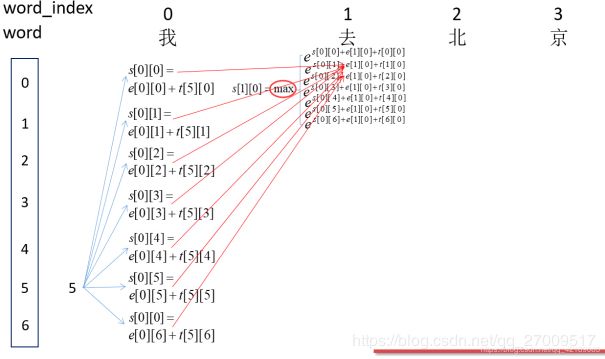
label_index为0时有7中可能,每种可能都要计算。
score[1][4] = score[0][4]+emit[1][4]+T[4][4]
因为刚开始为即为5,然后word_index为0的时候的所有可能的得分,即s[0][0],s[0][1]…s[0][6]中间的那部分。然后计算word_index为1的所有s[1][0],s[1][1]…s[1][6]的得分,这里以s[1][0]为例,即红箭头的焦点处:这里表示所有路径到这里的得分总和。
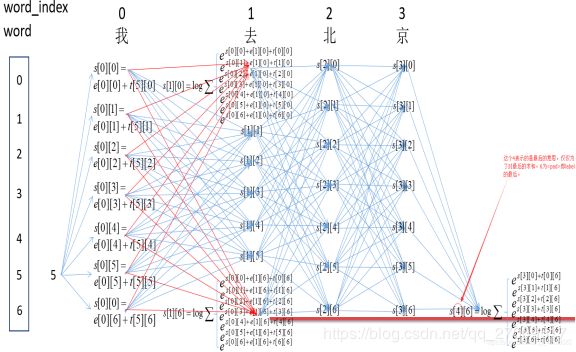
这里每个节点,都表示前面的所有路径到当前节点路径的所有得分之和。所以,最后的s[4][6]即为最终的得分之和,即:
计算gold分数,即:S(X,y) 这事只要通过此时的T和emit函数计算就能得出,计算公式上面已经给出了:
![]()
然后就是重复上述的求解所有路径的过程,将总和和gold的得分都求出来,得到loss,然后进行更新T,emit即可。(实现的话,其实emit是隐层输出,不是更新的对象,之后的实现会讲)
解码过程,就是动态规划,但是在这种模型中,通常叫做维特比算法。如图:
大概思路就是这次的每个节点不是求和,而是求max值和记录此max的位置。“去”这个词求的最大的label是上一个的label的index。
最后每个节点都求了出来,结果为:
最后,根据最后的节点,向前选取最佳的路径。过程为:最后的label为2,表示最后的上一个取得label的index是2,词“京”取index为2的结点。。