算法第四次作业-分支限界法求解作业分配问题
一、运行环境:
Win7、Spyder、Python3.7
二、运行过程说明:
数据文件格式:输入数据来源于文件,input_assign04_0*.dat。文件内是n*n矩阵的元素,每行的元素代表每个工人完成该任务所需要的时间,每列代表某个工人完成每个工作需要的时间,读出的数据放在嵌套了列表的列表matrix中。
输入格式:
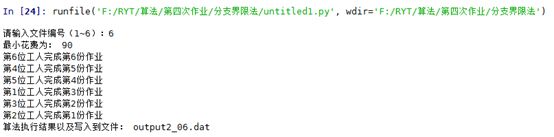
在Spyder中运行程序,输入测试数据集文件编号。
或者在cmd中:
![]()
输出:
三、算法设计
3.1问题描述:
n份作业分配给n个人去完成,每人完成一份作业。假定第i个人完成第j份作业需要花费cij时间,cij>0,1≦i,j≦n。试设计一个分支限界算法,将n份作业分配给n个人完成,使得总花费时间最少。
3.2解题思路:
(1)(估算下界,放到优先队列)从根节点开始向下搜索,在整个搜索过程中,每遇到一个结点,对其所有儿子结点计算它们的下界,把它们记录在结点表中。
(2)(从优先队列取最值,重复操作)从表中选取最小的结点,并重复上述过程。
(3)(叶节点是否是最优解的判定)当搜索到一个叶子节点,如果该节点的下界是结点表中最小的,那么该节点就是问题的最优解。否则,对下界最小的结点继续进行扩展。
下界估算方法(类似于贪心):
(1)假定k表示搜索深度,当k = 0,从根节点开始向下搜索。若将0号作业(j = 0)分配给第i位操作员(0 ≤ i ≤ n-1),其余作业分配给其余操作员,则所需时间至少为:第i位操作员完成第0号作业的时间 + 其余n-1项作业分配给其余n-1位操作员单独完成时所需最短时间之和。(下式中l是任意的,只要不等于i即可)
(2)下图中,若将第0号作业分配给第0位操作员,c00 = 3,此时所需时间下界为: 3 + 7(1号作业给其余三位操作员完成最短时间) + 6(2号作业给其余三位操作员完成最短时间) + 3(3号作业给其余三位操作员完成最短时间) = 19
(3)当搜索深度为k,前面第0, 1, ..., k-1号作业已经分别分配给编号i0, i1, ..., ik-1的操作员。令S = {0, 1, ..., n-1}表示所有操作员的编号集合;mk-1 = {i0, i1, ..., ik-1}表示作业已分配的操作员的编号集合。当把k号作业分配给编号为ik的操作员时,ik ∈ S - mk-1。显然,其下界为:
3.3数据结构的选择:
Node 类:#此类用来存放分支树上的所有有效节点
self.deep # 标记当前节点的深度
self.cost # 标记到达当前节点的总花费
self.father # 标记当前节点的父节点
self.value # 当前节点的花费
self.worker # 当前节点的任务由第几位工人完成
Worker 类:
max = 0 # 上界 通过贪心算法找出近似值
min = 0 # 下界 由每组的最小值组成
pt_nodes = [] # 存放可扩展的节点 FIFO
pt_flag = 0 # 标记队列是否被使用 用于结束算法
input_file = '' # 输入文件名
output_file = '' # 输出文件名
matrix = [] # 存放数据矩阵 行为单个任务 每个工人 完成所要的时间
n = 0 # 数据矩阵的大小 n*n
min_leaf_node = None # 消耗最小的节点
函数:
read_data_from_file # 从文件中读取数据
get_low_limit # 计算下界
get_up_limit # 计算上界
branch_limit # 执行分支界限算法
output_result # 结果输出到文件
四、算法详细描述:
4.1步骤
- 将数据用n*n的矩阵来描述 M[i,j]表示第i个任务由第j位工人完成所耗时间。
- 使用贪心算法计算一个近似的最优解作为上界。
- 最小值求和法得到最优解的下界。
- 针对第一个任务,检查每人耗时是否超过上界:
- 是:舍弃;
- 否:创建节点加入队列。
- 开始按先进先出的规则处理队列元素。
- 若当前节点是子节点,判断是否是最优节点;
- 若当前节点不是子节点,检查累积上下一个任务每人的耗时后是否超过上界 :
- 是:舍弃;
- 否:继续创建节点加入队列。
- 当队列处理完毕后,层层遍历最优节点的父节点,输出结果。
4.2伪代码:
根据限界函数计算目标函数的下界down;采用贪心法得到上界up;
将待处理节点表PT初始化为空
for ( i = 1 ; i < n ; i ++ )
x[i]=0;
k=1;i=0;
while(k>=1)
x[k]=1;
while(x[k]<=n)
if工人k分配任务x[k]不发生冲突,则:
根据 第k行的最小值计算目标函数值lb;
若lb<=up,则将I,lb存储在表PT中;
x[k]=x[k]+1;
if k==n && 叶子结点的lb值在表PT中最小:
print 该叶子结点对应的最优解
else if k==n && 叶子结点的lb值在表PT中不是最小:
up=表PT中的叶子结点最小的lb值;
将表PT中超过目标函数界的节点删除;
i=表PT中lb最小的节点的x[k]值;
k=表PT中lb最小的节点的k值;k++; 4.3使用python编写的代码:
# -*- coding: utf-8 -*-
"""
Created on Fri Nov 8 08:59:25 2019
@author: Administrator
"""
# 分支节点类
class Node:
def __init__(self):
self.deep = 0 # 标记该节点的深度
self.cost = 0 # 标记到达该节点的总消费
self.father = None # 标记该节点的父节点
self.value = 0 # 本节点的消费值
self.worker = None # 本节点的该任务由第几位工人完成
# 分支算法执行类
class Worker:
input_file = '' # 输入文件名
output_file = '' # 输出文件名
n = 0 # 数据矩阵的大小 n*n
matrix = [] # 存放数据矩阵 行为单个任务 每个工人 完成所要的时间
max = 0 # 上界 通过贪心算法找出近似值
min = 0 # 下界 由每组的最小值组成
pt_nodes = [] # 存放可扩展的节点
pt_flag = 0 # 标记队列是否被使用 用于结束算法
min_leaf_node = None # 消耗最小的节点
# 初始化参数
def __init__(self, input_file, output_file):
self.input_file = input_file
self.output_file = output_file
self.read_data()
self.n = len(self.matrix)
self.get_low_limit()
self.get_up_limit()
# 从文件中读取数据 初始化数据矩阵
def read_data(self):
with open(self.input_file) as source:
for line in source:
data_cluster = line.split(',')
temp = []
for value in data_cluster:
temp.append(int(value))
self.matrix.append(temp)
# 获取数据下界 最小值之和
def get_low_limit(self):
for i in range(self.n):
self.min += min(self.matrix[i])
# 获取数据上界 贪心算法
def get_up_limit(self):
# 初始化工人使用标记
worker_mark = []
for i in range(self.n):
worker_mark.append(0)
# 贪心算法 取得 近似最优解
for i in range(self.n):
temp = self.matrix[i]
min_value = 5000
index = 0
for k in range(self.n):
if worker_mark[k] == 0 and min_value > temp[k]:
min_value = temp[k]
index = k
worker_mark[index] = 1 # 标记工人是否被分配
self.max += min_value # 累积上限值
# 分支界限算法
def branch_limit(self):
if self.pt_flag == 0: # 从第一层开始
for i in range(self.n):
time = self.matrix[0][i]
if time <= self.max: # 没达到上限,创建节点,加入队列
node = Node()
node.deep = 0
node.cost = time
node.value = time
node.worker = i
self.pt_nodes.append(node)
self.pt_flag = 1
while self.pt_flag == 1: # 永久循环 等队列空了在根据条件判断来结束
if len(self.pt_nodes) == 0:
break
temp = self.pt_nodes.pop(0) # 先进先出
present_node = temp
total_cost = temp.cost
present_deep = temp.deep
# 初始化工人分配标记
worker_mark = []
for i in range(self.n):
worker_mark.append(0)
# 检查本节点下的作业分配情况
worker_mark[temp.worker] = 1
while temp.father is not None:
temp = temp.father
worker_mark[temp.worker] = 1
if present_deep + 1 == self.n: # 最后一排的叶子节点 直接分配结果
if self.min_leaf_node is None:
self.min_leaf_node = present_node
else:
if self.min_leaf_node.cost > present_node.cost:
self.min_leaf_node = present_node
else:
children = self.matrix[present_deep + 1]
# 检查本节点的子节点是否符合进入队列的要求
for k in range(self.n):
if children[k] + total_cost <= self.max and worker_mark[k] == 0:
node = Node()
node.deep = present_deep + 1
node.cost = children[k] + total_cost
node.value = children[k]
node.worker = k
node.father = present_node
self.pt_nodes.append(node)
# 输出算法执行的结果
def output(self):
file = open(self.output_file,'a')
temp = self.min_leaf_node
print("最小花费为:",temp.cost)
file.write('最少花费为:' + str(temp.cost) + '\n')
print("第"+str(temp.worker+1) + "位工人完成第"+str(temp.deep+1) + "份作业")
file.write('第'+str(temp.worker+1) + '位工人完成第'+str(temp.deep+1) + '份作业\n')
while temp.father is not None:
temp = temp.father
print("第"+str(temp.worker+1) + "位工人完成第"+str(temp.deep+1) + "份作业")
file.write('第' + str(temp.worker + 1) + '位工人完成第' + str(temp.deep + 1) + '份作业\n')
print('算法执行结果以及写入到文件:', self.output_file)
x=input("请输入文件编号(1~6):")
input_file = 'input_assgin04_0'+x+'.dat'
output_file = 'output2_0'+x+'.dat'
# 初始化算法执行类
worker = Worker(input_file, output_file)
# 执行分支界限算法
worker.branch_limit()
# 输出结果
worker.output()五、算法分析
时间复杂度:
由于本问题的解空间是排列树,这类排列树通常有n!个叶结点。所以最坏时间复杂度是O(n!);但是分支界限法首先扩展解空间树中的上层结点,并采用限界函数,有利于实行大范围剪枝,同时,根据限界函数不断调整搜索方向,选择最有可能取得最优解的子树有限进行搜索。所以,当选择了节点的合理扩展顺序以及设计了一个好的衔接函数,分支界限法可以快速得到问题的解。
空间复杂度:
在最坏情况下,分支限界法需要的空间复杂度是指数阶。分支限界法的高效率是以付出一定代价为基础的,其工作方式也造成了算法设计的复杂性。首先,一个更好的限界函数通常需要花费更多的时间计算相应的目标函数值,而且,对于具体的问题实例,通常需要进行大量试验,才能确定一个好的限界函数;其次,由于分支限界法对接空间树种节点的处理是跳跃式的,因此,在搜索到某个叶子节点得到最优值时,为了从该叶子结点求出对应的最优解中的各个分量,需要对每个扩展节点保存该节点到根节点的路径,或者在搜索过程中构建搜索经过的树结构,这使得算法的设计较为复杂;再次,算法要维护一个待处理结点表PT,并且需要在表PT中快速查找取得极值的结点,等等。这都需要较大的存储空间。