(学习笔记)机器学习:决策树
决策树
简介:决策树的原理与游戏 ‘20个问题’ 类似,用户输入一系列数据,然后给出结论。
下面给出5数据,后面程序测试数据以此为例
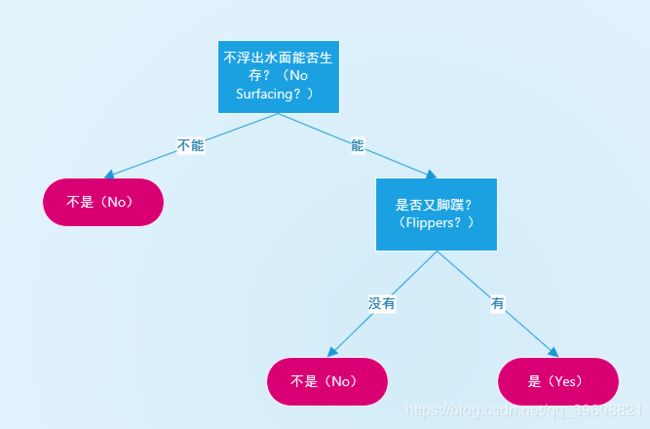
以 ‘能否不浮出水面生存’ 和 ‘是否有脚蹼’ 两个特性判断 该生物是否是鱼
------No surfacing?--------Flippers?-----------Fish?--------
- ----Yes -----------------Yes --------------Yes ---------
- ----Yes -----------------Yes --------------Yes --------
- ----Yes -----------------No ---------------No --------
- ----No ------------------Yes --------------No --------
- ----No ------------------No ---------------No ----------
下图为流程图形式的决策树
决策树的特性
优点:计算复杂度不高,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能产生过度匹配问题。
适用数据类型:数值型,标称型。
一些补充概念
-
信息增益:在划分数据集之前之后,信息发生的变化。
-
信息增益的用处:知道如何计算信息增益,就可以计算每个特征值划分数据集获得的信息增益,从而知道获得最高信息增益的特征。
-
熵(香农熵):定义为信息的期望值。
#熵的公式
H(X)=−∑p(xi)log(p(xi)) (i=1,2,…,n)
其中X 表示的是随机变量,随机变量的取值为(x1,x2,…,xn) ,p({x_i}) 表示事件xi发生的概率,且有∑p(xi)=1 。信息熵的单位为bit。
Python计算给定数据集的香农熵
from math import log
def calcShannonEnt(dataSet):
numEntries = len(dataSet) #总实例个数
labelCounts = {} #新建字典,键值是最后一列的数值
for featVec in dataSet: #数据集中筛选键值不存在于新建字典中的扩展字典并加入字典
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0 #计算并返回熵
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
可以创建函数,自输入数据测试一下上面的代码
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers'
return dataSet, labels
划分数据集
通过度量划分数据集的熵,可以判断当前是否正确的划分了数据集
#按照给定特征划分数据集
#三个参数分别代表:‘带划分的数据集’,‘划分数据集的特征’,‘需要返回的特征的值’
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
使用前面两个函数,构造函数来选择最好的划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals: #计算每种划分的信息熵
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain): #选择最好的划分方式
bestInfoGain = infoGain
bestFeature = i
return bestFeature
创建树
#参数分别是 数据集 和 标签列表
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0
if len(dataSet[0]) == 1
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
-#代码中两个if语句是递归的两个停止条件,分别为 ‘所有标签完全相同’ 和 ‘遍历完所有特征后仍然不能将数据集划分为仅包含唯一类别的分组’
#由于第二个退出递归条件无法简单的返回唯一的类标签,使用majorityCnt函数返回出现次数最多的类别
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
《Machine Learning in Action》 - Peter Harrington