插值算法:最近邻插值、双线性插值、双三次插值
文章目录
- 1.最近邻插值
- 2.双线性插值
- 3.双三次插值
- 代码实践:
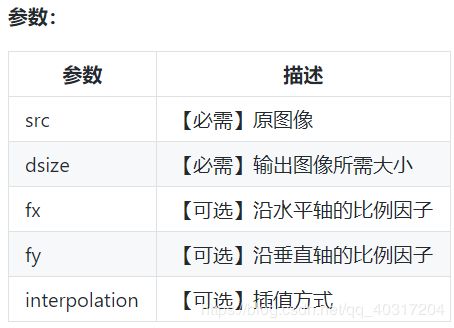
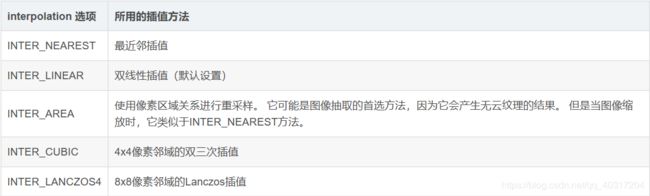
- cv2.resize简介:
在图像处理中,平移变换、旋转变换以及放缩变换是一些基础且常用的操作。这些几何变换并不改变图象的象素值,只是在图象平面上进行象素的重新排列。
在一幅输入图象 [ u , v ] [u,v] [u,v]中,灰度值仅在整数位置上有定义。然而,输出图象[x,y]的灰度值一般由处在非整数坐标上的 ( u , v ) (u,v) (u,v)值来决定。
这就需要插值算法来进行处理,常见的插值算法有最近邻插值、双线性插值和三次样条插值。
1.最近邻插值
定义:目标各像素点的灰度值代替源图像中与其最邻近像素的灰度值。
最近临插值算法优点是算法简单,易于实现,但是缺点是由于相邻像素点的像素值相同,容易出现色块现象。
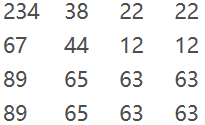
假设源图像(Source):

坐标的确定是从左上角为零开始,向右向下增大分别为x,y。
如果要将以上图像放大四倍,即从3×3->4×4,如何操作?
s r c X = d s t X ∗ ( s r c W i d t h / d s t W i d t h ) srcX=dstX* (srcWidth/dstWidth) srcX=dstX∗(srcWidth/dstWidth)
s r c Y = d s t Y ∗ ( s r c H e i g h t / d s t H e i g h t ) srcY = dstY * (srcHeight/dstHeight) srcY=dstY∗(srcHeight/dstHeight)比如要求目标图的(0, 3)的像素值,即第一行第四列的坐标的像素值:
( 0 ∗ ( 3 / 4 ) , 3 ∗ ( 3 / 4 ) ) = > ( 0 ∗ 0.75 , 3 ∗ 0.75 ) 四 舍 五 入 后 — — > ( 0 , 2 ) (0*(3/4),3*(3/4))=>(0*0.75,3*0.75) 四舍五入后 ——> (0,2) (0∗(3/4),3∗(3/4))=>(0∗0.75,3∗0.75)四舍五入后——>(0,2)即目标图的(0, 3)的像素值,等于源图像的(0, 2)的像素值。
由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值。
2.双线性插值
根据待求点P相邻最近4个点的像素值,计算出P点的像素值。
如下图所示:
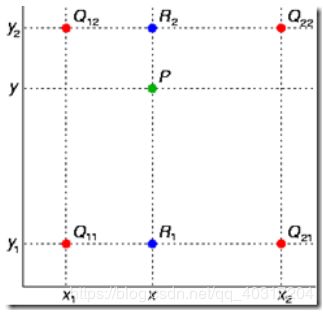
已知Q12,Q22,Q11,Q21,但是要插值的点为P点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对P点进行插值,这就是所谓的双线性插值。(f ( * )为 * 点处像素值)
在x,y方向分别进行插值计算,最后对P点进行插值计算:
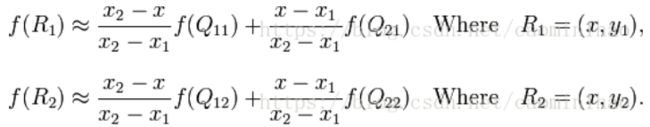
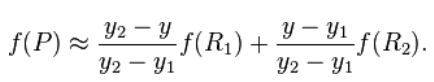
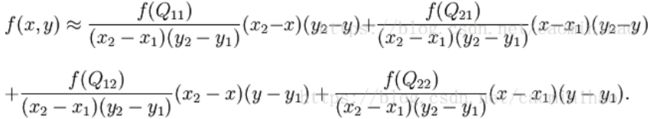
得到P点的像素 f(x, y)
3.双三次插值
假设源图经过缩放K倍之后得到目标图,若原图A的大小为mn,则目标图B的大小为(Km)*(K*n)。
设A已知,B未知。
要求出目标图B中像素点的值:必须先找出源图像A中对应的像素,再根据源图像中对应的像素距离最近的16个像素点作为计算目标图像像素值的参数,利用BiCubic基函数S(x)求出16个像素点的权重,图B像素(x,y)的值就等于16个像素点的加权叠加。


S(x)即为权重,我们要求出x,从而求出S(X)。
对于像素点的行与列的系数分开计算。
例如:
a00距离P(x+u,y+v)的距离为(1+u,1+v),因此a00的横坐标权重 i_0=W(1+u),纵坐标权重 j_0=W(1+v),a00 对 B(X,Y) 的贡献值为:(a00像素值)* i_0* j_0。因此,a0X的横坐标权重分别为W(1+u),W(u),W(1-u),W(2-u);ay0的纵坐标权重分别为W(1+v),W(v),W(1-v),W(2-v);B(X,Y)像素值为:
B ( X , Y ) = ∑ i = 0 3 ∑ i = 0 3 a i j × W ( i ) × W ( j ) B(X, Y)=\sum_{i=0}^{3} {\sum_{i=0}^{3} {a_{ij}×W(i)×W(j)}} B(X,Y)=i=0∑3i=0∑3aij×W(i)×W(j)
对待插值的像素点(x,y)(x和y可以为浮点数),取其附近的4x4邻域点(xi,yj), i,j = 0,1,2,3。按如下公式进行插值计算:
f ( x , y ) = ∑ i = 0 3 ∑ i = 0 3 f ( x i , y i ) × W ( x − x i ) × W ( y − y j ) f(x,y)=\sum_{i=0}^{3} {\sum_{i=0}^{3} {f(x_i,y_i)×W(x-x_i)×W(y-y_j)}} f(x,y)=i=0∑3i=0∑3f(xi,yi)×W(x−xi)×W(y−yj)
代码实践:
import cv2
if __name__ == "__main__":
img = cv2.imread(r'C:\Users\chenyiqun\Desktop\timg.jpg', cv2.IMREAD_UNCHANGED)
print('Original Dimensions : ', img.shape)
scale_percent = 30 # percent of original size
width = int(img.shape[1] * scale_percent / 100)
height = int(img.shape[0] * scale_percent / 100)
dim = (width, height)
# resize image
resized = cv2.resize(img, dim, interpolation=cv2.INTER_LINEAR)
fx = 1.5
fy = 1.5
resized1 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation=cv2.INTER_NEAREST)
resized2 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation=cv2.INTER_LINEAR)
resized3 = cv2.resize(resized, dsize=None, fx=fx, fy=fy, interpolation=cv2.INTER_CUBIC)
print('Resized Dimensions : ', resized.shape)
cv2.imshow("Resized image", resized)
cv2.imshow("INTER_NEAREST image", resized1)
cv2.imshow("INTER_LINEAR image", resized2)
cv2.imshow("INTER_CUBIC image", resized3)
cv2.waitKey(0)
cv2.destroyAllWindows()从如下结果可以看出,INTER_NEAREST的效果是不如INTER_LINEAR和INTER_CUBIC的:
cv2.resize简介:
cv2.resize(src,dsize,dst=None,fx=None,fy=None,interpolation=None)
参考文章:
https://blog.csdn.net/caomin1hao/article/details/81092134?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-6&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-6