背包dp总结
背包每次写每次都不会,再次又学习了基础的背包,后面的遇到再补吧
01背包
首先对于每种物品可以取后者不取,所以我们可以写出记忆化的代码
\(dp[pos][val]\)表示容量为\(val\),选后\(pos\)个物品的最大价值
每种物品取或不取,然后暴搜记忆化
int V, n;
int w[110];
int c[110];
int dp[1010][1010];
int dfs(int pos, int val) {
if (pos == n + 1) return 0;
if (~dp[pos][val]) return dp[pos][val];
int tmp1 = -1, tmp2 = -1;
tmp1 = dfs(pos + 1, val);
if (val >= w[pos])
tmp2 = dfs(pos + 1, val - w[pos]) + c[pos];
dp[pos][val] = max(tmp1, tmp2);
return dp[pos][val];
}
int main() {
scanf("%d %d", &V, &n);
memset(dp, -1, sizeof(dp));
for (int i = 1; i <= n; i++) {
scanf("%d %d", &w[i], &c[i]);
}
dfs(1, V);
printf("%d\n", dp[1][V]);
}同样根据取与不取,我们可以用
\(dp[i][j]\)表示前\(i\)个物品恰好装满容量为\(j\)的背包的最大价值
可以写出状态转移方程
\[ dp[i][j]= \begin{cases} dp[i-1][j], & \text{if j < w[i]} \\ dp[i-1][j-w[i]]+c[i], & \text{if j >= w[i]} \end{cases} \]
int V, n;
int w[110];
int c[110];
int dp[110][1010];
int main() {
scanf("%d %d", &V, &n);
for (int i = 1; i <= n; i++) {
scanf("%d %d", &w[i], &c[i]);
}
for (int i = 0; i <= n; i++) dp[i][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
if (j >= w[i])
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + c[i]);
else
dp[i][j] = dp[i - 1][j];
}
}
printf("%d\n", dp[n][V]);
}可以看出都是由\(i-1\)推过来的,所以我们可以滚掉第一维。
\(dp[j]\)表示容量为\(j\)的最大价值
\[ dp[j]=max(dp[j], dp[j-w[i]]+c[i]) \]
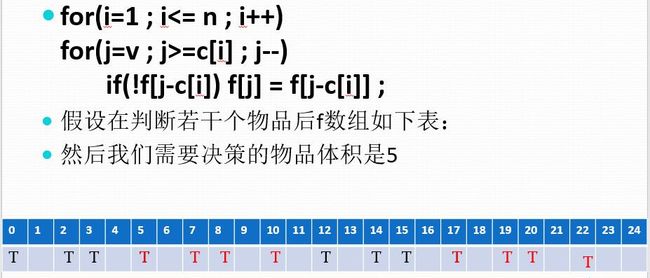
这里考虑如果还是顺序的遍历,那么一个物品可能会被多次使用:
这样就能保证\(dp[j]\)是\(dp[i-1][j]\),\(dp[j-w[i]]+c[i]\)是\(dp[i-1][j-w[i]]+c[i]\)
int V, n;
int w[110];
int c[110];
int dp[1010];
int main() {
scanf("%d %d", &V, &n);
for (int i = 1; i <= n; i++) {
scanf("%d %d", &w[i], &c[i]);
}
for (int i = 1; i <= n; i++) {
for (int j = V; j >= w[i]; j--) {
dp[j] = max(dp[j], dp[j - w[i]] + c[i]);
}
}
printf("%d\n", dp[V]);
}