字典树与01字典树详解

【镇楼】

  不满足于粗浅的表面了解字典树吗，今天！由我给大家带来！字典树与01字典树的解析！！

目录

【引入】

【字典树】

【01字典树】

【引用参考】

---

 

【引入】

字典是干啥的？查找字的。那么字典树顾名思义，自然也就是起查找作用的一种树，查找的是啥？单词。

我们先来看以下两个问题：

1、给出n个单词和m个询问，每次询问一个单词，回答这个单词是否在单词表中出现过。

答：用map记录即可，短小精悍。

2、给出n个单词和m个询问，每次询问一个前缀，回答询问是多少个单词的前缀。

答：map，把每个单词拆开。

judge：n<=200000，TLE！

这就需要一种高级数据结构——Trie树（字典树）

【字典树】

字典树显然是一棵树，那么如何建树呢？树的边表示什么呢？结点又表示什么呢？

【建树】

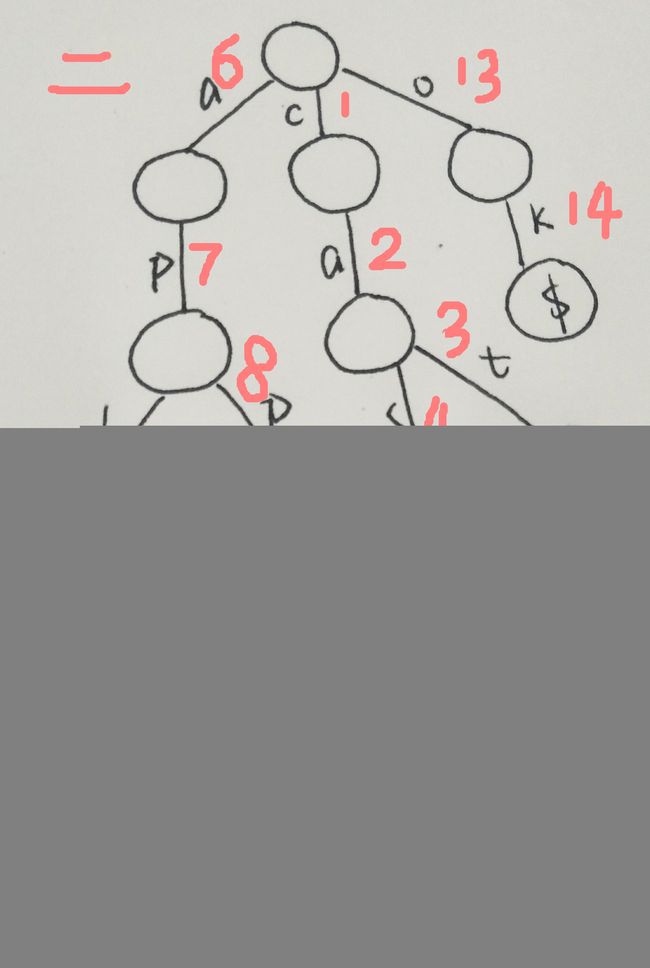
我们对 cat，cash，app，apple，aply，ok 建一颗字典树，建成之后如下图一所示。

从图中可以看出，执行的操作是：从左到右扫这个单词，如果字母在相应根节点下没有出现过，就插入这个字母；否则沿着字典树往下走，直到单词的下一个字母没有出现过或者遍历结束。

          

这就产生一个问题：往哪儿插？我们需要给它指定一个位置，那就需要给每个字母编号。

【插入】 

我们设数组trie[i][j]=k，表示编号为i的节点的第j个孩子是编号为k的节点。

什么意思呢？这里有2种编号，一种是i，k表示节点的位置编号，这是相对于整棵树而言的；另一种是j，表示节点i的第j的孩子，这是相对于节点i而言的。请结合图二理解。

还有一种编号方式，因为每个节点最多有26个子节点，我们可以按他们的字典序从0-25编号。trie[i][j]=true|false，表示编号为i的节点的第j个孩子是否已经存在。请结合图三。

通过上面的图我们可以清晰的看到：

1.字典树的边表示字母。

2.字典树的结点用于存放一个特殊字符，记录从根节点到这个节点为止这样一个单词。

3.有相同前缀的单词共用前缀结点，所以我们可以快速跑出最长公共前缀、最多单词的公共前缀等等。

4.第二种编号方式是由单词字母所在的位置即深度和字母的字典序所决定的，每个节点的子节点都应该从0编到25，会造成比较大的空间浪费。而第一种编号方式显然比较适用于大部分情况，节约空间，用到哪个分哪个。

【查找】

从左往右依次扫描每个字母，顺着字典树往下找，能找到这个字母，往下走，否则结束查找，即没有这个前缀；前缀扫完则表示有这个前缀。可以查找前缀、单词是否出现过，或者查找前缀出现的次数(开一个数组sum[]存储)，查找某个单词等等。

【例题】

下面让我们结合题目来理解代码实现：

以 hdu 1251 统计难题 为例

题意：给定一些单词，再给出一些前缀询问这些前缀出现次数？

代码：

#include 
using namespace std;
const int maxn=1e6+10;
int sum[maxn]={0};
int trie[maxn][26];
char s[15];
int pos=1;
void add() //插入
{
    int c=0;
    for(int i=0;s[i];i++){
        int x=s[i]-'0';
        if(trie[c][x]==0) //没出现过就增加一个结点
            trie[c][x]=pos++;
        c=trie[c][x]; //下一个结点
        sum[c]++; //更新前缀出现次数
    }
}
void query() //查找
{
    int c=0;
    for(int i=0;s[i];i++){
        int x=s[i]-'0';
        if(trie[c][x]==0){ //找不到说明没出现过
            printf("0\n");
            return;
        }
        c=trie[c][x]; //下一个结点
    }
    printf("%d\n",sum[c]);
}
int main()
{
    while(gets(s)&&s[0]!=NULL)
        add();
    while(gets(s))
        query();
    return 0;
}

【01字典树】

01字典树主要用于解决求异或最值的问题。

01字典树和普通的字典树原理类似，只不过把插入字符改成了插入二进制串的每一位（0或1）。

让我们通过一段简短的代码理解一下实现过程。

int pos=0;
void add(int num) //插入
{
    int c=0;
    for(int i=31;i>=0;i--){
        int op=((num>>i)&1);
        if(!trie[c][op])
            trie[c][op]=++pos;
        c=trie[c][op];
        val[c]++;
    }
    val[u]=num; //节点值为x，到这里是一个数
}
int query(int num)
{ //查询所有数中和num异或结果最大的数
    int c=0;
    for(int i=31;i>=0;i--){
        int op=((num>>i)&1);
        if(trie[c][op^1]) //优先走和当前位不同的路
            c=trie[p][op^1];
        else c=trie[p][op];
    }
    return val[c];
}
int query(int num)
{ //查询所有数中和num异或结果最小的数
    int c=0;
    for(int i=31;i>=0;i--){
        int op=((num>>i)&1);
        if(trie[c][op]) //优先走和当前位相同的路
            c=trie[p][op];
        else c=trie[p][op^1];
    }
    return val[c];
}

通过上面的代码，我们可以发现：

1. 01字典树是一棵最多32层的二叉树，其每个节点的两条边分别表示二进制的某一位的值是 0 还是 1，将某个路径上边的值连起来就得到一个二进制串。

2.节点个数为 1 的层（最高层）节点的边对应着二进制串的最高位。

3.以上代码中，trie[i] 表示一个节点，trie[i][0] 和 trie[i][1] 表示节点的两条边指向的节点，val[i] 表示节点的值。

4.每个节点主要有 4个属性：节点值、节点编号、两条边指向的下一节点的编号。

5.节点值 val为 0 时表示到当前节点为止不能形成一个数，否则 val[i]=数值。

6.可通过贪心的策略来寻找与x异或结果最大(最小)的数，即优先找和x的二进制的未处理的最高位值不同(相同)的边对应的点，这样保证结果最大。 

【例题】

下面让我们结合题目来理解代码实现

以hdu 4825 Xor Sum 为例：

给出n个数和m次询问，每次询问给出一个数x，问在n个数中哪个数与x异或值最大？

代码：

#include 
using namespace std;
const int maxn=1e6+10;
int a[maxn],vis[maxn*3];
int trie[maxn*3][3];
int pos;
void add(int x,int id)
{
    int c=0,op;
    for(int i=31;i>=0;i--){
        op=((x&(1<=0;i--){
        op=((x&(1<

【拓展】

我们还可以写出带删除的字典树。只要定义一个数组记录当前节点的访问次数，如果次数为1且为要删去的数字的访问节点，那么置0即可。这里不再赘述。 

【引用参考】

浅谈Trie树

01字典树 详解

【推荐】

01字典树专题（题目合集）