优先级队列(极其值得一看的内容讲解)

9.优先级队列

Tips:本文的所有涉及代码均来自于邓俊辉老师,文中插图也是其PPT中,可以结合其对应视频课学习

9.1 需求与动机

• 循优先级访问的实际情况

  • 离散事件
  • 操作系统:任务调度/中断处理/MRU
  • 输入法:词频调整

• 作为底层数据结构所支持的高效操作是很多高效算法的基础

  • 内部、外部、在线排序
  • 贪心算法 ： Huffman编码,Kruskal算法

ADT：

template <typename T>
struct PQ{//priority queue 
    virtual void insert(T)=0;
    virtual T getMax()=0;
    virtual T delMax()=0;
};//作为ADT的PQ有多种实现方式,各自的效率及适用场合也不尽相同

实际上

• stack和queue，都是PQ的特例----优先级完全取决于元素的插入顺序
• steap和Queap，也是PQ的特例----插入和删除的位置受限

9.2 优先级队列的实现

• 使用哪种数据结构来实现优先级队列？

  首先明确一件事，对于优先级队列而言是由一个变量表征优先级的大小，所以重点在于是不是能再允许的时间复杂度$O(n)$将数据按照优先级的顺序插入或者删除。

首先联想的是向量(vector),

但是可想而知,并不满足我们对于时间复杂度的要求,插入满足需求,但是删除远远不满足.

如果我们使用排序向量(sorted vector)

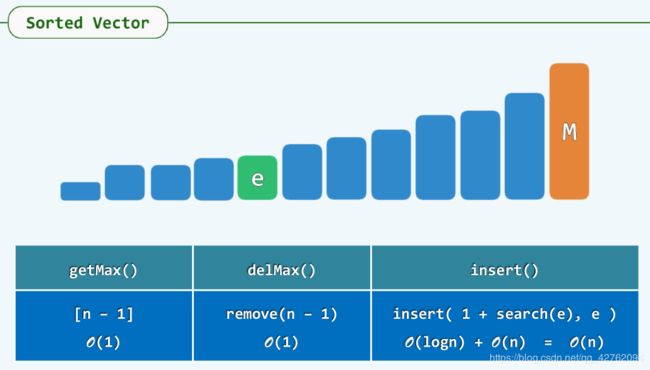
这样insert就不满足需求了.

而后考察list,sorted list 均不满足实际的需要,或者这么说,可以实现但是过于浪费效率.

后来想到了 BBST – avl,splay,redblack,他们的insert,delete所需的时间复杂度为$O(\log n)$满足要求,但是由于PQ仅仅需要部分功能,而BBST远远超出PQ的需求

因为PQ的delmax只需寻找极值元，并没必要维护所有元素之间的全序关系，仅仅需要偏序。

1. 结构

• 逻辑上，等同于完全二叉树
• 物理上，直接借助向量实现

注意:优先级队列的唯一规则为 H[parent(i)] > H[i]

由于是完全二叉树（向量）就有一些可以直接使用的数学关系如下；

#define Parent(i) (((i) - 1 ) >> 1)
#define LChild(i) ( 1 + ( (i) >> 1) )
#define RChild(i) ( ( 1 + (i) ) << 1)

• 内部结点的最大秩为$[\frac{n-2}{2}]=[\frac{n-3}{2}]$
  
  **key:**上面0,1,2是向量的秩关系,表征的是对应点的位置,并不是对应点的大小关系,虽然elem[0]必定是最大值,但是elem[1]就不一定大于elem[2].

对应的代码为:

template <typename T>
struct PQ_ComplHeap : public PQ<T>,public Vector<T>
{
    //实现PQ的基本接口
    void insert(T);
    T getMax()
    {
        return _elem[0];
    }
    T delMax();
    //批量建堆
    PQ_ComplHeap(T* Arr,Rank n )
    {
        copyFrom(A , 0 , n );
        heapify(_elem , n );
    }
    Rank precolateDown(T* arr, Rank n,Rank i);
    Rank precolateUp(T* arr ,Rank i);
    void  heapify(T* A,Rank n);//Floyd建堆算法
};

2.接口 : 插入

template <typename T>
void PQ_ComplHeap<T>::insert(const T e)
{
    Vector<T>::insert(e); //注意调用的是 vector的insert
    percolateUp(_elem,_size - 1);
}
template <typename T>
Rank PQ_ComplHeap<T>::precolateUp(T* arr,Rank  i)
{
    while(0 < i)
    {//在抵达堆顶之前,反复地
        Rank j = Parent( i );//考察[i]之父亲[j]
        if(lt(arr[ i ] , arr[ j ]))//一旦父子顺序,上滤旋即完成;否则
            break;
        swap(arr[ i ],arr[ j ]); //将父子换位,并且继续考察上一层
        i = j ;//改变i的值
    } //while
    return i; //返回上滤最终抵达的位置 
}

理解:

本质是向量,将e直接插入到尾,而后自底向上进行上滤处理,直到堆顶(对应的秩为 0 ),将新插入的与其父亲对比,如果新插入优先级大于父亲优先级则交换,两种情况结束循环 1.交换到堆顶 2.某一级父亲的优先级大于儿子优先级.

效率:

• e在上滤过程中，只可能与祖先们交换

• 完全树必平衡，e的祖先不超过$O(\log n)$个

• 故知插入操作可在$O(\log n)$时间内完成

• 就数学期望而言,实际效率往往远远更高…

3.接口 :删除

1.对于删除,由于优先级队列的特性,优先最高的为根节点,需最先删除,但是后续出现的两个子树该怎么解决?
选两个孩子最大者,那后续该如何?

依次进行,将孩子最大者上移,但是这样所做的最大问题是,很大可能破坏了完全二叉树的基本结构.
2.如何解决 ?
将最后的一个点移到最前面,由于不满足父亲优先级大于儿子,所以需要下滤,直至叶子.

3.如何下滤?
我们首先需要考虑的是,基于完全二叉堆的情况下,父亲是优先级大于孩子的,当然此时堆顶是肯定不满足的条件的,但是他的两个孩子肯定是剩余最大的(两个孩子的大小是没有明确的大小关系的),所以将其中较大的推为堆顶,是在逐渐符合规则的,同时堆顶也是优先级最大的,所以核心方法是找到其孩子的最大者,而后重复进行
代码:

template <typename T>
T PQ_ComplHeap<T>::delMax()
{
    //摘除堆顶,代之以末词条
    T maxElem = _elem[0] ;
    _elem[0] = _elem [-- _size ];
    //从新堆顶实施下滤
    precolateDown(_elem , _size , 0)
    //返回此前备份的最大词条
    return  maxElem;
}
template <typename T>
Rank PQ_ComplHeap<T>::precolateDown(T* arr,Rank n,Rank i )
{
    Rank bc =  getBiChild(arr,i);
    Rank ext = (n-2)/2;//叶子和内部节点的分界线
    while(arr[i] < arr[bc])//当父亲大于bigchild时结束循环
    {
        swap(arr[i],arr[bc]);
        i = bc ;
        if(i > ext )
            break;
        bc = getBiChild(arr,i);
    }
    return i ;
}
template <typename T>
Rank getBiChild(T* arr,Rank i)
{
    Rank lc = LChild(i);
    Rank rc = RChild(i);
    return (arr[lc] >arr[rc]) ? lc : rc;
}

效率:

• e在每一高度至多交换一次累计交换不超过$O(\log n)$次
• 通过下滤,可在$O(\log n)$时间内
• 删除堆顶节点,并-整体重新调整为堆
• 在基于统计的概念的情况下,所需的时间复杂度是小于$O(\log n)$的

4.批量建堆

Q:对于一些老的数据我们需要堆化,一个一个的假如就有点浪费时间了,如何更有效率的建立一个完全二叉堆?

A:Floyd建堆法

Q:何为Floyd建堆法?

A:

Way1.面对初始问题我们会想到一个解决办法:先将数组copy进堆,而后利用上滤的方法从第一点依次上滤恢复整个堆的顺次关系,这个方法是完全可行的,但是可以预见的时间复杂度会很高,因为会将每个节点进行上滤而单个节点上滤的时间复杂度为$O(\log n)$,所有节点则时间复杂度上是远远大于$O(n)$的,达到$o(n\log n)$有这个时间我可以做一个排序了,所以需要换一种思路.

Way2.上滤—下滤,从堆顶开始下滤,而且由于叶子是没有的儿子的所以仅下滤仅限于内部节点,从内部节点开始下溢,则此为Floyd建堆法.

  PQ_ComplHeap(T* Arr,Rank n )
    {
        copyFrom(A , 0 , n ); //将对应的数组copy仅堆
        heapify(_elem , n ); //建堆
    }

template <typename T>
void heapify(T* A,Rank n)
{
    for(int i = n/2 - 1 ; 0 <= i ; i--)//这里为什么从n/2-1开始 完全二叉树的性质
    {
        percolateDown(A,n,i);
    }
}

效率:

• 每个内部节点所需的调整时间，正比于其高度而非深度
• 不失一般性，考查满树：n=2h+1-1
• 所有节点的高度总和$O(n)$,时间复杂度亦是如此.

5.应用 :堆排序

时间复杂度分析:

• J.Williams,1964

  ​ 初始化:heapify(),$O(n)$

  ​ 迭代:delmax(),$O(\log n)$

  ​ 不变性:$H\le S$

• $O(n)+n\times O(\log n)=O(n\log n)$

空间复杂度分析:

• 由于完全二叉堆本质上是向量,所以完全可以实现在有限的空间情况下进行排序–就地

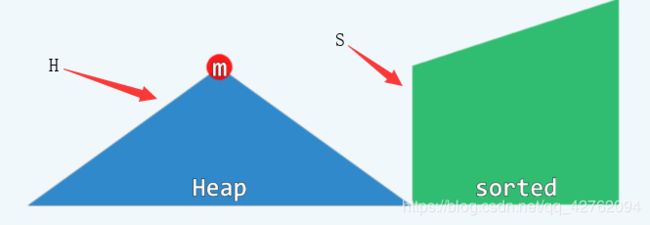
基本方法就是:m = H.delMax()---->S.insert(m)代码为:

template <typename T> //对向量区间[lo,hi)做就地堆排序
void Vector<T>::heapSort(Rank lo,Rank hi)
{
    //建堆区域
    T* A = _elem + lo; 
    Rank n = hi - lo ;
    heapify(A,n);//建立一个堆O(n)
    while(0 < --n) //n作为循环变量,标识数目
    {
        swap(A[0],A[n]); //代表的是H.delMax(),S.insert
        percolaateDown(A,n,0);//对堆顶元素下滤
    }
}

9.2 左式堆

1.动机

Q:上图中的完全二叉堆,对于插入删除操作已经给出了很好的答卷,但是如果需要将两个不相关联的堆如何合并?

A:一般的想法是:将较为大的堆作为基础而后将较小的堆插入,我们计算一下这样的时间复杂度为?

​ 不妨假设一下$|A|=n\ge m=|B|$

• 方法一: A.insert(B.delMax()) = $O(m\times (\log m+\log (n+m)))$

显然过于耗费时间了.

• 方法二 :有了上面的基础,我们之前说过一个批量建堆的方法,为什么不用一下?事实上是完全可以的.

  先使用向量的方法结合A和B为C,而后对于C进行批量建堆,$O(m+n)$

• 方法三 :上述方法其实已经基本满足需求但是我们可不可以要求一下更好的性能,比如$O(\log n)$

  ​ 有,我们这种新的设计方法就是如此.

2.结构

• C.A.Crane,1972 : 保持堆序性,附加新条件,使得在堆合并过程中,只需调整少量的节点 :$O(\log n)$

• 新条件 = 单侧倾斜: 节点分布偏向于左侧

  ​ 合并操作只涉及右侧

为了实现上述的结构,需再理解几个相关的概念:

1.空节点路径长度(NULL Path Length):

类似于红黑树的概念引入外部节点,如图三角形节点所示,而后规定

• $npl(外部节点)=npl(NULL)=0$
• $npl(x)=1+min\{npl(lc(x),npl(rc(x))\}$

中文表示而言就是 : $npl(x)$ = x到外部节点的最近距离 =以x为根的最大满子树的高度 (注意这个最大满子树的高度)

2.左式堆 = 处处左倾

• 对于任何节点x,都有:

  $npl(lc(x))\ge npl(rc(x))$推而广之$npl(lc(x))=npl(rc(x))+1$

• 左式堆的子堆,必是左式堆

• 左倾性与堆序性,相容而不矛盾

3.右侧链(rChain)

定义 : 从节点x出发,一直沿右分支前进.

• 特别地,rchain(x)的终点,必为全堆中最浅的外部节点

  • $npl(r)=|rChain(r)|=d$

  • 必存在一个以r为根、高度为d的满子树

• 右侧链长为d的左式堆,至少包含

  • $2^d-1$个内部节点
  • $2^{d+1}-1$个节点

• 反之,在包含n个节点的左式堆中,右侧链长度 $d \le [\log_2(n+1) - 1]=O(\log n) $

3.实现

直接给出代码:

template <typename T>
class PQ_LeftHeap:public PQ<T>,public BinTree<T>
{
    T getMax()
    {
        return _root->data;
    }
    void insert(T);
    T delMax(); // 均基于同一的合并操作
}
//模板函数:合并
template <typename T>
static BinNodePosi(T) merge(BinNodePosi(T) , BinNodePosi(T) );

合并思想:

1.先比较a和b的优先级,如果b大于a,则两者交换—>所有的节点的优先级对比保证堆序性.

2.而后将b作为其右子树,同时再讲$a_r$的根与b比较如果不符合关系$npl(lc)\ge npl(rc)$交换–>保证左倾性

算法实现代码:

template <typename T>
static BinNodePosi(T) merge(BinNodePosi(T) a, BinNodePosi(T) b)
{
    //递归基
    if( !a )
        return b ;
    if( !b )
        return a ;
    if(a->data < b->data)
        swap(a,b);
    a->rc = merge(a->rc,b);//递归
    a->rc->parent = a ; //修正孩子的父亲
    if(!a->lc ||a->lc->npl < a->rc->npl)
        swap(a->lc,a->rc);
    a->npl = a->rc ? 1 + a->rc->npl : 1;//修正npl值
    return a ;//返回合并后的堆顶
}

分析:

​ 整个递归代码写的异常巧妙,由于比较优先级是从上到下,而比较npl是从下至上,但是前面的递归执行到最后一步(即将返回时,这时完成了before的内容)会执行11~15行的代码,从而开始比较npl的值.

4.插入和删除

对于左式堆而言插入和删除,就是merge函数的又一应用.

1.插入

即可看做一个仅有一个元素的新堆,与旧堆合并.

template <typename T>
void PQ_LeftHeap<T>::insert(T e)
{
    _root = merge(_root,new BinNode<T>(e,NULL));
    _size++;
}

2.删除

将_root删除后,则其右孩子和左孩子又组成了两个堆.

template <typename T>
T PQ_LeftHeap<T>::delMax()
{
    BinNodePosi(T) lHeap = _root->lc ;
    if(lHeap)
        lHeap->parent = NULL;
    BinNodePosi(T) rHeap = _root->rc ;
    if(rHeap)
        rHeap->parent = NULL ;
    T e = _root->data ; 
    delete(_root);
    _size -- ;
    _root = merge(lHeap,rHeap);
    return e;
}