李宏毅机器学习笔记01

线性回归

好记性不如烂笔头，梳理了一下知识点，方便自己忘记时，巩固知识
首先是机器学习的三个步骤：
Step1: Model
Step2: Goodness of Function
Step3: Find the best function

Step1:
本次是分析宝可梦（神奇宝贝！！！）进化前的CP值对进化后的CP值的预测。
线性回归的分析，这里先假设model是f(xⁿ_cp) = b + w * xⁿ_cp

Step2:
建立一个随时函数来判断方法的好不好
L(f) = ∑¹⁰_{n =1}(y’ⁿ - f(xⁿ_cp))
转化一下变成w,b的Loss函数
L(w,b) = ∑¹⁰_{n =1}(y’ⁿ - (b + w * xⁿ_cp))
接下来要做的事情就是找到一组w,b是的L(w,b)最小
w*,b* = argmin_w,bL(w,b)

Step3:
这里使用的是梯度下降（爬山法）的方法
这里使用一元的介绍一下梯度下降
1,随机选出w⁰
2,计算该点在L(w)上的斜率，就是算这一点的微分，结果记为d，
如果d > 0向左移，减小w;如果d < 0向右移，增大w
3,w¹ = w⁰ - λ * ∂L(w)/∂w(w⁰代入计算)
4，直到w^T = 0时结束，得到w值

该方法存在一个问题，就是局部最优解。比如在你实际例子中当w^T 无限趋近与0了，你有可能认为它要到最终目的地了，就停止了。但是它可能与最终点还有一段距离（函数太过平滑）。或者函数有好几个谷值，可能这个谷值不是真正的最小点是一个局部最小点。
二元的计算方法也是类似的，无非就是对w,b分别微分，知道两者都等于0.得到结果。
以下是程序计算的结果：
w = 2.668084232234726
b = -187.67102850934788
当然可以计算一下误差（我计算的平均误差）：
误差值平均为：
89.74
下面是实验图：

当然可能不是一次相关，可能是二次相关
我们改变一下模型：
y_data = b + w1 * x_data + w2 * (x_data * x_data)

重新计算结果为：
w1 =
1.541282082460168
w2 =
0.002011369085724176
b_1 =
-90.96508009986827
误差值是：
误差值平均为：
47.84357293710826

实验图为：

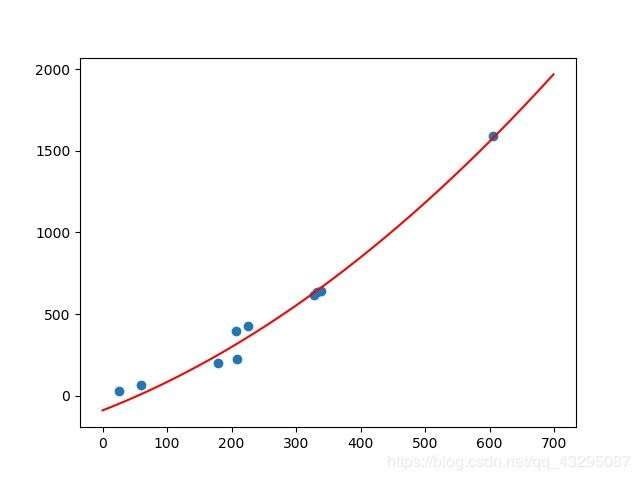
我们可以看到好像二次比一次误差要小一点，图片上看好像是更加拟合一些。
但是其实我这个结果不一定是正确的，为什么呢？
1.我这是模型没有经过测试，不光有训练数据集，还要验证数据集和测试数据集。因为宝可梦的CP值，没有现车的数据集，所以我就懒得去收集了。。。。。。想做的话可以去官网，写个爬虫，爬一下，分析一下。
2.可能在梯度下降的过程中有局部最优解的问题。

下面是python 代码，可以实现一下：

#宠物小精灵进化前后CP值分析
import numpy as np
import matplotlib.pyplot as plt

x_data = [338.,333.,328.,207.,226.,25.,179.,60.,208.,606.,]
y_data = [640.,633.,619.,393.,428.,27.,197.,66.,226.,1591.,]
plt.plot(x_data,y_data,'o')
plt.savefig('D:/机器学习/宝可梦CP值散点图.jpg')
plt.show()


#y_data = b + w * x_data
#假设随机的b,w
b = -120
w = -4
Ir = 1 #learning rate

iteration = 100000
#设置一个个性learning rate
Ir_b = 0
Ir_w = 0

for i in range(iteration):
    b_grad = 0.0
    w_grad = 0.0
    for n in range(len(x_data)):
        #计算偏微分
        b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0
        w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]

    Ir_b = Ir_b + b_grad ** 2
    Ir_w = Ir_w + w_grad ** 2
    b = b - Ir/np.sqrt(Ir_b) * b_grad
    w = w - Ir/np.sqrt(Ir_w) * w_grad
    
print("w = ",w)
print('b = ',b)

x1 = np.arange(0,700,1)
y1 = w * x1 + b
plt.plot(x_data,y_data,'o')
plt.plot(x1,y1,'orange')
plt.savefig('D:/机器学习/宝可梦CP值线性回归.jpg')
plt.show()


#接下来计算一下误差值
bias = 0.0
for i in range(len(x_data)):
    y_now = 2.7 * x_data[i] -188.4
    bias += abs(y_data[i] - y_now)
print("误差值平均为：")
print(bias/len(x_data))

#模型改为二次的看看
#y_data = b + w1 * x_data + w2 * (x_data * x_data)
#随机初始化值
b_1 = -120
w1 = -4
w2 = 1
Ir = 1 #learning rate
iteration = 100000

#设置一个个性learning rate
Ir_b_1 = 0
Ir_w1 = 0
Ir_w2 = 0
for i in range(iteration):
    b1_grad = 0.0
    w1_grad = 0.0
    w2_grad = 0.0
    for n in range(len(x_data)):
        b1_grad = b1_grad - 2 * (y_data[n] - (b_1 + w1 * x_data[n] + w2 * x_data[n] * x_data[n])) * 1.0
        w1_grad = w1_grad - 2 * (y_data[n] - (b_1 + w1 * x_data[n] + w2 * x_data[n] * x_data[n])) * x_data[n]
        w2_grad = w2_grad - 2 * (y_data[n] - (b_1 + w1 * x_data[n] + w2 * x_data[n] * x_data[n])) * (x_data[n] * x_data[n])
    Ir_b_1 = Ir_b_1 + b1_grad ** 2
    Ir_w1 = Ir_w1 + w1_grad ** 2
    Ir_w2 = Ir_w2 + w2_grad ** 2
    b_1 = b_1 - Ir/np.sqrt(Ir_b_1) * b1_grad
    w1 = w1 - Ir/np.sqrt(Ir_w1) * w1_grad
    w2 = w2 - Ir/np.sqrt(Ir_w2) * w2_grad

print("w1 = ")
print(w1)
print('w2 = ')
print(w2)
print('b_1 = ')
print(b_1)
x2 = np.arange(0,700,1)
y2 = w1 *x2 + w2 * x2 * x2 + b_1
plt.plot(x_data,y_data,'o')
plt.plot(x2,y2,'red')
plt.savefig('D:/机器学习/宝可梦CP值线性(二次)回归.jpg')
plt.show()

#误差值分析一下
bias1 = 0.0
for i in range(len(x_data)):
    y_now = w1 * x_data[i] + w2 * x_data[i] * x_data[i] + b_1
    bias1 += abs(y_data[i] - y_now)
print("误差值平均为：")
print(bias1/len(x_data))

自己还做了一个验证梯度下降的找最优解的python程序，也分享一下：

#宠物小精灵进化前后CP值分析
import numpy as np
import matplotlib.pyplot as plt

x_data = [338.,333.,328.,207.,226.,25.,179.,60.,208.,606.,]
y_data = [640.,633.,619.,393.,428.,27.,197.,66.,226.,1591.,]
plt.plot(x_data,y_data,'o')
plt.show()

#y_data = b + w * x_data
x = np.arange(-200,-100,1)
y = np.arange(-5,5,0.1)
z = np.zeros((len(x),len(y)))
X,Y = np.meshgrid(x,y)
#建立损失函数
for i in range(len(x)):
    for j in range(len(y)):
        b = x[i]
        w = y[i]
        z[j][i] = 0
        for n in range(len(x_data)):
            z[j][i] = z[j][i] + (y_data[n] - b - w * x_data[n]) ** 2
        z[j][i] = z[j][i] / len(x_data)

#假设随机的b,w
b = -120
w = -4
Ir = 1 #learning rate
iteration = 100000

b_history = [b]
w_history = [w]

#设置一个个性learning rate
Ir_b = 0
Ir_w = 0

for n in range(iteration):
    b_grad = 0.0
    w_grad = 0.0
    for n in range(len(x_data)):
        #计算偏微分
        b_grad = b_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * 1.0
        w_grad = w_grad - 2.0 * (y_data[n] - b - w * x_data[n]) * x_data[n]

    Ir_b = Ir_b + b_grad ** 2
    Ir_w = Ir_w + w_grad ** 2
    b = b - Ir/np.sqrt(Ir_b) * b_grad
    w = w - Ir/np.sqrt(Ir_w) * w_grad

    b_history.append(b)
    w_history.append(w)
plt.contourf(x,y,z,50,alpha = 0.5,cmap = plt.get_cmap('jet'))
plt.plot([-188.4],[2.67],'x',ms = 12,markeredgewidth = 3,color = 'orange')
plt.plot(b_history,w_history,'o-',ms = 3,lw = 1.5,color = 'black')
plt.xlim(-200,-100)
plt.ylim(-5,5)
plt.xlabel(r'$b$',fontsize = 16)
plt.ylabel(r'$w$',fontsize = 16)
plt.savefig('D:/机器学习/梯度下降.jpg')
plt.show()

下面是实验结果图：

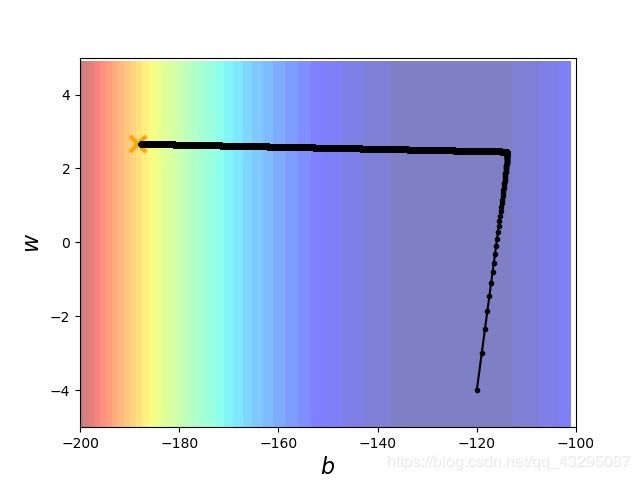
图中的X就是我们上面算的最优解（一次的那个解），从图中我们可以看见是怎么一步一步找到最优解的。可以自己去试试，这里的learning rate利用了Adagrad的方法，给每个参数分配自己的learning rate。

最后提一句：那么我们的误差来自哪里呢？
其实就是来自于bias and variance。
bias:离中心的偏差距离，
variance:离散程度，每个点与中心点的偏移程度

下一章介绍，bias and variance以及Gradient Descent的数学原理