计算理论之正则语言

在计算理论中，为了建立一个易于处理的数学理论，我们采用称为计算模型（computational model）的理想计算机来描述。本文从最简单的模型开始，它称为有穷状态机（finite state machine）或有穷自动机（finite automaton）。

如果想进一步了解本文所述知识，可以参阅机械工业出版社《计算理论导引》第一部分第一章。

有穷自动机

有穷自动机是描述能力和资源极其有限的计算机的模型。但是一台存储如此少的计算机也能完成很多有用的事情了。事实上，我们的日常生活中处处都有它的应用场景。

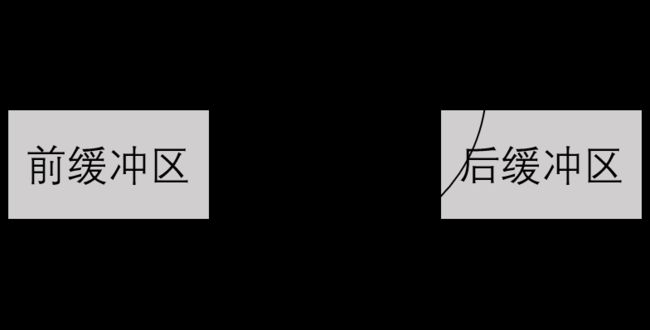
如下图所示，假设我们有一扇门，门只能向右侧单向打开。左侧是门的前缓冲区，右侧是门的后缓冲区。当前缓冲区检测到有人的时候，门就会打开以允许人流通过。当后缓冲区检测有人的时候，门会保持当前的状态以防止碰到后面的人。

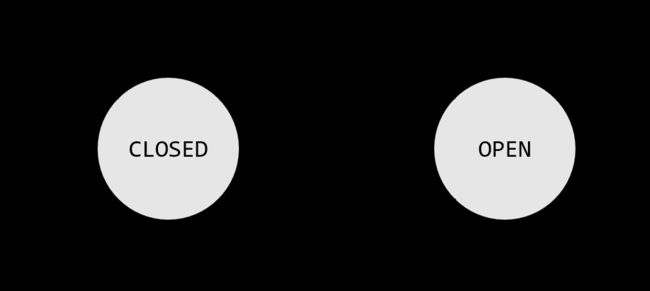
现在有一个控制器去控制这一扇门。控制器有且仅有两个状态：开（OPEN）、关（CLOSED）。我们有四种可能的输入：FRONT（仅前缓冲区有人）、REAR（仅后缓冲区有人）、BOTH（前后缓冲区都有人）、NEITHER（前后缓冲区都没人）。

控制器根据它的输入从一个状态转移到另一个状态。当它处于CLOSE状态且接收到输入FRONT时，转到OPEN状态，否则仍处于CLOSED状态；当它处于OPEN状态且接收到输入NEITHER时，转到CLOSED状态，否则保持OPEN状态。

用有穷自动机理论来处理这一控制器是很好的方法。下图是用有穷状态机表述的控制器。它是一台存储器只有一位的计算机，因为这就足以记录其所处的状态了。而另外一些设备可能具有容量稍微大一点的存储器，比如电梯的控制器等等。

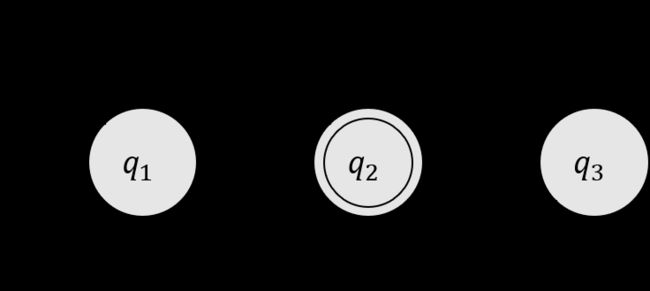
下面用一个更加抽象化的例子来描述一个有穷状态机，我们假设它叫 $M$ 。下图被称为 $M$ 的状态图（state diagram），它有三个状态，记作 $q_1,q_2,q_3$ 。起始状态（start state） $q_1$ 用一个指向它的无出发点的箭头表示，接受状态（accept state） $q_2$ 带有双圈。从一个状态指向另一个状态的箭头称为转移（transition）。

当这个自动机接收到输入字符串，例如 $1101$ 时，它处理这个字符串并且产生一个输出。输出是接受或拒绝。处理从 $M$ 的起始状态开始。自动机从左至右一个接一个地接收输入字符串的所有符号。读到一个符号之后， $M$ 沿着标有该符号的转移从一个状态移动到另一个状态。当读到最后一个符号时产生输出。

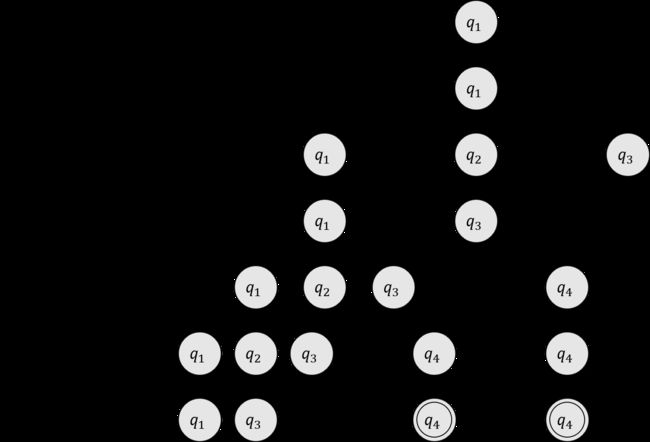
例如，输入 $1101$ ， $M$ 的处理步骤如下：

1. 开始时处于状态 $q_1$ 。
2. 读到 $1$ ，状态从 $q_1$ 转移到 $q_2$ 。
3. 读到 $1$ ，状态从 $q_2$ 转移到 $q_2$ 。
4. 读到 $0$ ，状态从 $q_2$ 转移到 $q_3$ 。
5. 读到 $1$ ，状态从 $q_3$ 转移到 $q_2$ 。
6. 输出接受，因为在输入字符串的末端 $M$ 处于接受状态 $q_2$ 。

用这台机器对各式各样的输入字符串进行检验，得知它接受且仅接受在最后一个 $1$ 的后面接偶数个 $0$ 的 $01$ 串。若 $A$ 是 $M$ 接受的全部字符串集合，则称 $A$ 是机器 $M$ 的语言，记作 $L(M)=A$ 。又称 $M$ 识别 $A$ 。一台机器可能接受若干字符串，但是它永远只能识别一个语言。如果机器不接受任何字符串，那么它仍然识别一个语言，即空语言 $\varnothing$ 。

下面给出有穷自动机的形式化定义。

有穷自动机是一个五元组 $(Q,\Sigma ,\delta ,q_0,F)$ ，其中

1. $Q$ 是一个有穷集合，称为状态集。
2. $\Sigma$ 是一个有穷集合，称为字母表。
3. $\delta :Q\times \Sigma \to Q$ 是状态转移函数。
4. $q_0\in Q$ 是初始状态。
5. $F\subseteq Q$ 是接受状态集合。

设 $M=(Q,\Sigma ,\delta ,q_0,F)$ 是一台有穷自动机， $w=w_1{w}_2\cdots w_n$ 是一个字符串且 $w_i\in \Sigma ,\forall i$ 。如果存在状态序列 $r_0,r_1,\cdots ,r_n\in Q$ 满足下述条件：

1. $r_0=q_0$
2. $\delta (r_i,w_{i+1})=r_{i+1},i=0,\cdots ,n-1$
3. $r_n\in F$

则称 $M$ 接受 $w$ 。

如果 $A=\{w|M\text{ 接受 }w\}$ ，则称 $M$ 识别语言 $A$ 。

如果一个语言被一台有穷自动机识别，则称它是正则语言（regular language）。

下面介绍正则语言上的运算。

设 $A$ 和 $B$ 是两个语言，定义正则运算并（union）、连接（concatenation）和星号（star）如下：

1. 并：$A\cup B=\{x|x\in A\vee x\in B\}$
2. 连接： $A\circ B=\{xy|x\in A\wedge y\in B\}$
3. 星号： $A^{\ast }=\{x_1{x}_2\cdots x_k|k\in {\mathbb{N}}^{\ast }\wedge (\forall i)(x_i\in A)\}$

并运算就是把 $A$ 和 $B$ 中的所有字符串合并在一个语言中。连接运算以所有可能的方式把 $A$ 中的一个字符串接在 $B$ 中的一个字符串前面，从而产生新语言中的所有字符串。星号运算把 $A$ 中的任意个字符串以任意顺序连接在一起得到新语言中的一个字符串。不管 $A$ 是什么，空串 $\epsilon$ 总是 $A^{\ast }$ 的一个成员。

正则运算都是封闭的。其中并运算的封闭性可以用构造性证明，证明过程如下：

证明：

设 $M_1=(Q_1,\Sigma ,{\delta }_1,q_1,F_1)$ 识别语言 $A_1$ ， $M_2=(Q_2,\Sigma ,{\delta }_2,q_2,F_2)$ 识别语言 $A_2$ 。下面我们将构造一个识别 $A_1\cup A_2$ 的自动机 $M=(Q,\Sigma ,\delta ,q_0,F)$ 。

令 $$\begin{gathered} Q=Q_1\times Q_2 \\ \delta (⟨r_1,r_2⟩,a)=⟨{\delta }_1(r_1,a),{\delta }_2(r_2,a)⟩ \\ {q}_0=⟨q_1,q_2⟩ \\ F=\{⟨r_1,r_2⟩|r_1\in F_1\vee r_2\in F_2\} \end{gathered}$$ 构造完毕。

至于其他两种运算封闭性的证明，需要借助下文的非确定性的概念。

非确定性

到现在为止，在我们的讨论中，计算的每一步都按照唯一的方式跟在前一步的后面。当机器处于给定的状态并读入下一个输入符号时，可以知道机器的下一个状态是什么——它是确定的。因此，称这是确定型计算（deterministic computation）。在非确定型（nondeterministic）机器中，任何一点的下一个状态都可能存在若干个选择。

下图所示即为一台非确定型有穷自动机。

确定型有穷自动机（简称DFA）与非确定型有穷自动机（简称NFA）之间的区别是显而易见的。第一，DFA的每一个状态对于字母表中的每一个符号总是恰好有一个转移箭头射出。然而上图违反了这条规则。状态 $q_1$ 对于 $0$ 有一个射出的箭头，而对于 $1$ 有两个射出的箭头； $q_2$ 对于 $0$ 有一个箭头，而对于 $1$ 没有箭头。在NFA中，一个状态对于字母表中的每一个符号可能有任意个射出的箭头。第二，在DFA中，转移箭头上的标号都取自字母表的符号，而上图的NFA中有一个带有标号 $\epsilon$ 的箭头。一般说来，NFA中从一个状态可能射出任意个带有标号 $\epsilon$ 的箭头。

为了将不确定性纳入有穷自动机中，NFA用并行运算来表示多个可能情况。对于从某个状态接受同一个输入引出的多个箭头，NFA会对于每一个箭头建立一个自己的备份，并且并行地向下执行所有的备份。如果某个备份在某个状态时接收到了一个没有对应转移的输入，则这个备份和与之相关的分支就会自动结束。最后，如果机器的某一个备份在输入的末端处于接受状态，则这台NFA接受输入字符串。对于标有 $\epsilon$ 的箭头，它表示，不用读任何输入，机器自动分裂出一个备份，且每一个带 $\epsilon$ 的箭头都会产生一份独立的备份。

考虑上面给出的NFA，下图描绘了它读取输入 $010110$ 的计算。

经过不同字符串的多次实验，我们发现上述NFA接受所有含有 $101$ 或 $11$ 作为子串的字符串。因此，我们还可以用一个DFA来等价地表述它。事实上我们即将会证明，任意一台NFA都会有一台DFA与之等价。

在证明这一点以前，我们首先给出非确定型有穷自动机的形式化定义：

非确定型有穷自动机是一个五元组 $(Q,\Sigma ,\delta ,q_0,F)$ ，其中

1. $Q$ 是有穷的状态集；
2. $\Sigma$ 是有穷的字母表；
3. $\delta :Q\times {\Sigma }_{\epsilon }\to \mathcal{P}(Q)$ 是转移函数；
4. $q_0\in Q$ 是起始状态；
5. $F\subseteq Q$ 是接受状态集。

设 $N=(Q,\Sigma ,\delta ,q_0,F)$ 是一台NFA， $w$ 是字母表 $\Sigma$ 上的一个字符串。如果能把 $w$ 写成 $w=y_1{y}_2\cdots y_m$ 的形式，其中 $\forall i,y_i\in {\Sigma }_{\epsilon }$ ，并且存在状态序列 $r_0,r_1,\cdots ,r_m\in Q$ 满足下述三个条件：

1. $r_0=q_0$
2. $r_{i+1}\in \delta (r_i,y_{i+1}),i=0,1,\cdots ,m-1$
3. $r_m\in F$

则称 $N$ 接受 $w$ 。

如果两台机器识别同样的语言，则称它们是等价的。下面我们证明NFA和DFA的等价性。

我们仍然使用构造性证明。设 $N=(Q,\Sigma ,\delta ,q_0,F)$ 是识别语言 $A$ 的一台NFA，要构造一台DFA识别 $A$ 。我们记这个DFA为 $M=(Q^{\prime },\Sigma ,{\delta }^{\prime },q_0^{\prime },F^{\prime })$ 。我们构造的主要思想是把NFA的多线程变为含有多个“单元状态”的状态集合。

定义 $\mathcal{P}(Q)$ 上的函数 $E$ ，对于 $Q$ 的一个子集 $R$ ， $E(R)$ 表示从 $R$ 的成员出发沿着 $0$ 个或多个 $\epsilon$ 箭头可以到达的状态集合。

令 $$\begin{gathered} Q^{\prime }=\mathcal{P}(Q) \\ {\delta }^{\prime }(R,a)=\bigcup _{r\in R}E[\delta (r,a)] \\ {q}_0^{\prime }=E(\{q_0\}) \\ {F}^{\prime }=\{R\in Q^{\prime }|R\cap F̸=\varnothing \} \end{gathered}$$ 得证。

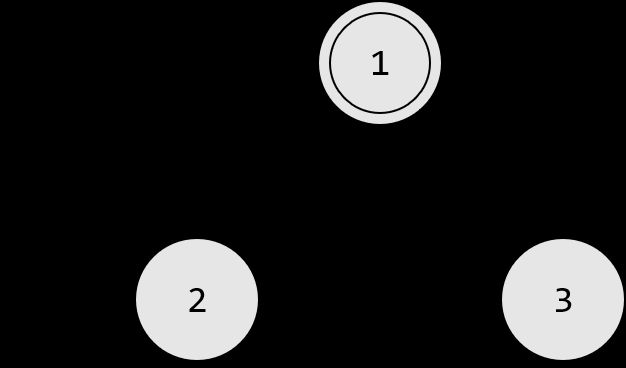
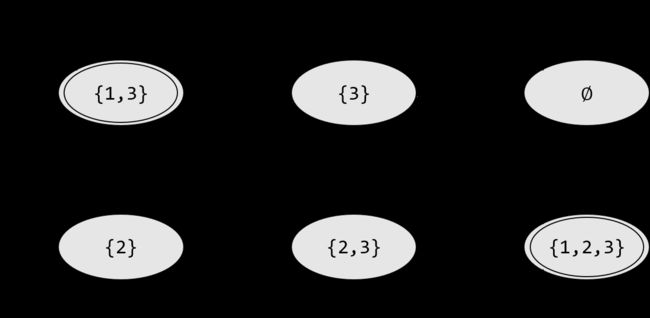
下面给出两台等价的有穷自动机，左边是NFA，右边是与之等价的DFA。

下面我们使用非确定性来证明正则运算的封闭性。

对于并运算的封闭性：

设 $N_1=(Q_1,\Sigma ,{\delta }_1,q_1,F_1)$ 识别 $A_1$ ，并且 $N_2=(Q_2,\Sigma ,{\delta }_2,q_2,F_2)$ 识别 $A_1$ 。我们构造识别 $A_1\cup A_2$ 的 $N=(Q,\Sigma ,\delta ,q_0,F)$ ：

1. $Q=\{q_0\}\cup Q_1\cup Q_2$ 。
2. $q_0$ 是新添加的状态。
3. $F=F_1\cup F_2$ 。
4. 对于每一个 $q\in Q$ 和每一个 $a\in {\Sigma }_{\epsilon }$ ， $$\delta (q,a)=\{\begin{array}{rlr}& {\delta }_1(q,a)& q\in Q_1\\ & {\delta }_2(q,a)& q\in Q_2\\ & \{q_1,q_2\}& q=q_0,a=\epsilon \\ & \varnothing & q=q_0,a̸=\epsilon \end{array}$$

对于连接运算的封闭性：

设 $N_1=(Q_1,\Sigma ,{\delta }_1,q_1,F_1)$ 识别 $A_1$ ，并且 $N_2=(Q_2,\Sigma ,{\delta }_2,q_2,F_2)$ 识别 $A_1$ 。我们构造识别 $A_1\circ A_2$ 的 $N=(Q,\Sigma ,\delta ,q_0,F)$ ：

1. $Q=Q_1\cup Q_2$ 。
2. $q_0=q_1$ 。
3. $F=F_2$ 。
4. 对于每一个 $q\in Q$ 和每一个 $a\in {\Sigma }_{\epsilon }$ ， $$\delta (q,a)=\{\begin{array}{rlr}& {\delta }_1(q,a)& q\in Q_1,q\notin F_1\\ & {\delta }_1(q,a)& q\in F_1,a̸=\epsilon \\ & {\delta }_1(q,a)\cup \{q_2\}& q\in F_1,a=\epsilon \\ & {\delta }_2(q,a)& q\in Q_2\end{array}$$

对于星号运算的封闭性：

设 $N_1=(Q_1,\Sigma ,{\delta }_1,q_1,F_1)$ 识别 $A_1$ ，我们构造识别 $A_1^{\ast }$ 的 $N=(Q,\Sigma ,\delta ,q_0,F)$ ：

1. $Q=\{q_0\}\cup Q_1$ 。
2. $q_0$ 是新添加的状态。
3. $F=\{q_0\}\cup F_1$ 。
4. 对于每一个 $q\in Q$ 和每一个 $a\in {\Sigma }_{\epsilon }$ ， δ ( q , a ) = { δ 1 ( q , a ) q ∈ Q 1 , q ∉ F 1 δ 1 ( q , a ) q ∈ F 1 , a ≠ ε δ 1 ( q , a ) ∪ { q 1 } q ∈ F 1 , a = ε { q 1 } q = q 0 , a = ε ∅ q = q 0 , a ≠ ε \delta(q,a)=\left\{\begin{aligned} &\delta_1(q,a)&q\in Q_1,q\notin F_1\\ &\delta_1(q,a)&q\in F_1,a\ne \varepsilon\\ &\delta_1(q,a)\cup\{q_1\}&q\in F_1,a=\varepsilon\\ &\{q_1\}&q=q_0,a=\varepsilon\\ &\varnothing&q=q_0,a\ne \varepsilon \end{aligned}\right. δ(q,a)=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​​δ1​(q,a)δ1​(q,a)δ1​(q,a)∪{q1​}{q1​}∅​q∈Q1​,q∈/​F1​q∈F1​,a̸​=εq∈F1​,a=εq=q0​,a=εq=q0​,a̸​=ε​

正则表达式

用正则运算符构造描述语言的表达式叫做正则表达式。例如 $(0\cup 1)0^{\ast }$ 表示由一个 $0$ 或者一个 $1$ 后面跟着任意个 $0$ 的所有字符串组成的语言。

下面给出正则表达式的形式化定义：

称 $R$ 是一个正则表达式，如果 $R$ 是

1. $a$ ，这里 $a$ 是字母表 $\Sigma$ 中的一个元素；
2. $\epsilon$ ；
3. $\varnothing$ ；
4. $(R_1\cup R_2)$ ，这里 $R_1$ 和 $R_2$ 都是正则表达式；
5. $(R_1\circ R_2)$ ，这里 $R_1$ 和 $R_2$ 都是正则表达式；
6. $(R_1^{\ast })$ ，这里 $R_1$ 是正则表达式。

表达式中的括号可以略去。如果略去括号，计算按照下述有限顺序进行：星号，连接，并。

为便于描述，我们将 $R{R}^{\ast }$ 记作 $R^{+}$ ，将 $k$ 个 $R$ 中的串通过连接得到的串记作 $R^k$ 。

当想要明显地区分正则表达式 $R$ 和它描述的语言时，可以把 $R$ 描述的语言写成 $L(R)$ 。

就描述能力而言正则表达式和有穷自动机是等价的，以下是证明：

首先我们证明，如果一个语言可以用正则表达式描述，那么它是正则的。

设 $R$ 是一个正则表达式，现将 $R$ 转换成一台NFA，记作 $N$ 。考虑正则表达式定义中的六种情况：

1. $R=a$ 。则 $N=(\{q_1,q_2\},\Sigma ,\delta ,q_1,\{q_2\})$ ，其中 $\delta$ 的定义如下：若 $r̸=q_1$ 或 $b̸=a$ ，则 $\delta (q_1,a)=\{q_2\},\delta (r,b)=\varnothing$ 。
2. $R=\epsilon$ 。则 $N=(\{q_1\},\Sigma ,\delta ,q_1,\{q_1\})$ ，其中 $\forall r,b,\delta (r,b)=\varnothing$ 。
3. $R=\varnothing$ 。则 $N=(\{q\},\Sigma ,\delta ,q,\varnothing )$ ，其中 $\forall r,b,\delta (r,b)=\varnothing$ 。

至于后三种情况，只需使用正则语言类在正则运算下封闭性的证明中所给出的构造即可。

接着我们证明，如果一个语言是正则的，则可以用正则表达式描述它。

在证明之前，我们先引入一个新型的有穷自动机——广义非确定型有穷自动机，简称GNFA。

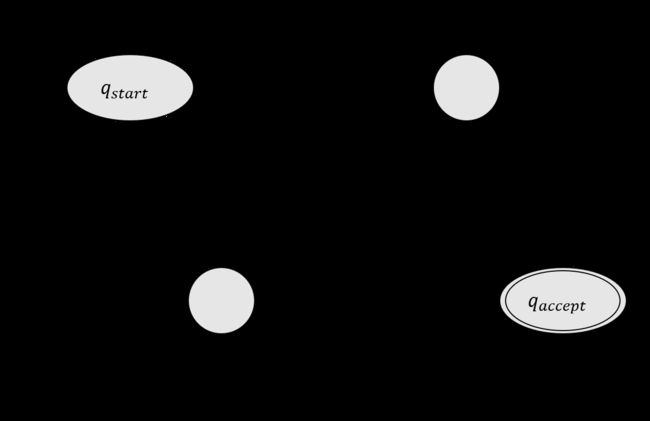
事实上，GNFA就是NFA，不过转移箭头可以用任何正则表达式作标号，而不是只能用字母表的成员或 $\epsilon$ 作标号。GNFA读入符号段，而不必一次只能读一个符号。下图是一个GNFA的例子：

为方便起见，我们约定GNFA具有下述特殊形式：

• 起始状态有射到其他每一个状态的箭头，但是没有从任何其他状态射入的箭头。
• 有唯一的一个接受状态，并且它有从其他每个状态射入的箭头，但是没有射到任何其他状态的箭头。此外，接受状态和起始状态不同。
• 除起始状态和接受状态外，每个状态到自身和其他每个状态都有一个箭头。

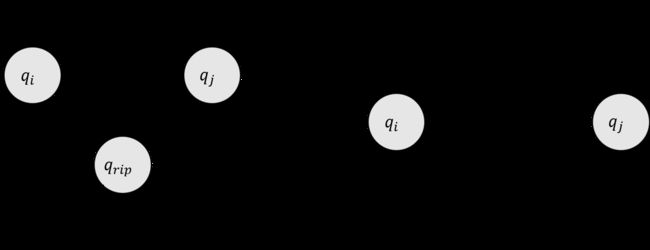
注意到性质中有一条“接受状态和起始状态不同”。因此一台GNFA至少有两个状态。而事实上，任何一台GNFA都可以等价地转化为一台只有两个状态的GNFA。我们假设这台GNFA有 $k>2$ 个状态。我们现在要删除一个状态 $q_{\text{rip}}$ ，然后对剩下的状态进行调整使之与原GNFA等价。 $q_{\text{rip}}$ 可以是除了起始状态和接受状态的所有状态。下图即为调整方法：

在原机器中，如果

1. 从 $q_i$ 到 $q_{\text{rip}}$ 有一个标记为 $R_1$ 的箭头
2. 从 $q_{\text{rip}}$ 到它自己有一个标记为 $R_2$ 的箭头
3. 从 $q_{\text{rip}}$ 到 $q_j$ 有一个标记为 $R_3$ 的箭头
4. 从 $q_i$ 到 $q_j$ 有一个标记为 $R_4$ 的箭头

那么在新机器中，从 $q_i$ 到 $q_j$ 的箭头的标记为 $(R_1)(R_2{)}^{\ast }(R_3)\cup (R_4)$ 。对从任一状态 $q_i$ 到 $q_j$ （包括 $q_i=q_j$ 在内）的每一个箭头都进行这样的改动，新的机器仍然识别原来的语言。

此外，我们可以很容易地把一个DFA转换成GNFA，只需进行以下操作即可：添加一个新的起始状态和一个新的接受状态，从新的起始状态到原起始状态连一个 $\epsilon$ 箭头，从每一个原接受状态到新的接受状态连一个 $\epsilon$ 箭头；如果一个箭头有多个标记，则把它替换成一个标记着原先标记的并集的箭头；最后，在没有箭头的状态之间添加标记 $\varnothing$ 的箭头。

转回我们的证明。我们需要证明的是，如果一个语言是正则的，则有一个正则表达式描述它。首先，如果一个语言是正则的，那么它能被一台DFA接受，因此它也能被一台GNFA接受，因此也能被一台仅含有两个状态的等价GNFA接受。设这台GNFA上从起始状态到接受状态的正则表达式为 $R$ ，则 $R$ 即为描述这个语言的正则表达式。证毕。

非正则语言

有穷自动机也是有其局限性的，有些语言不能被有穷自动机识别。比如，设语言 $B=\{0^n{1}^n|n\in \mathbb{N}\}$ 。如果想找一台识别 $B$ 的DFA，会发现这台机器看起来需要记住它在输入中读到了多少个 $0$ ，由于 $0$ 的个数没有限制，因此机器将不得不记住无穷多个可能。但用有穷自动机无法做到这一点。

不过这样的评判并不严谨，比如 $C=\{w|count(0)=count(1)\}$ 和 $D=\{w|count(01)=count(10)\}$ （其中 $count(x)$ 表示统计字符串 $x$ 在 $w$ 中出现的次数）这两个语言，看似很相像，但 $C$ 不是正则语言，而 $D$ 是正则语言。

因此我们引入了一个称为泵引理（pumping lemma）的定理。该定理指出，所有的正则语言都有一个特定值——泵长度（pumping length），语言中的所有字符串只要它的长度不小于泵长度，就可以被“抽取”。下面是泵引理的形式化表述：

若 $A$ 是一个正则语言，则存在一个数 $p$ （泵长度）使得，如果 $s$ 是 $A$ 中任一长度不小于 $p$ 的字符串，那么 $s$ 可以被分成三段， $s=xyz$ ，满足下述条件：

1. $x{y}^{i}z\in A,\forall i\in \mathbb{N}$
2. $|y|>0$
3. $|xy|⩽p$

其中 $|\cdot |$ 表示字符串的长度， $y^i$ 表示连续的 $i$ 个 $y$ 。

证明

设 $M=(Q,\Sigma ,\delta ,q_1,F)$ 是一台识别 $A$ 的DFA， $p$ 是 $M$ 的状态数。设 $s=s_1{s}_2\cdots s_n$ 是 $A$ 中长度为 $n$ 的字符串，这里 $n⩾p$ 。又设 $r_1,\cdots ,r_{n+1}$ 是 $M$ 在处理 $s$ 的过程中进入的状态序列，因而 $r_{i+1}=\delta (r_i,s_i),i=1,2,\cdots ,n$ 。该序列的长度为 $n+1$ ，不小于 $p+1$ 。根据抽屉原理，在该序列的前 $p+1$ 个元素中，一定有两个相同的状态。设第一个是 $r_j$ ，第二个是 $r_l$ 。由于 $r_l$ 出现在序列的前 $p+1$ 个位置中，而且序列是从 $r_1$ 开始的，故 $l⩽p+1$ 。此时，令 $x=s_1\cdots s_{j-1},y=s_j\cdots s_{l-1},z=s_l\cdots s_n$ 。由于 $x$ 把 $M$ 从 $r_1$ 带到 $r_j$ ， $y$ 把 $M$ 从 $r_j$ 带回到 $r_j$ ， $z$ 把 $M$ 从 $r_j$ 带到 $r_{n+1}$ ，而 $r_{n+1}$ 是一个接受状态，故对于 $i\in \mathbb{N}$ ， $M$ 接受 $x{y}^{i}z$ 。已知 $j̸=l$ ，故 $|y|>0$ ；又已知 $l⩽p+1$ ，故 $|xy|⩽p$ 。于是，满足泵引理的三个条件。证毕。

最后，作为示例，我们用泵引理证明几个语言不是正则语言。

首先证明 $B=\{0^n{1}^n|n\in \mathbb{N}\}$ 不是正则语言。

假设 $B$ 是正则的。令 $p$ 是其泵长度。选择 $s$ 为字符串 $0^p{1}^p$ ，则 $s$ 可以写成 $s=xyz$ 的形式。我们考虑以下三种情况：

1. $y$ 只包含 $0$ 。此时， $xyyz$ 中的 $0$ 比 $1$ 多，从而 $x{y}^{2}z\notin B$ ，矛盾。
2. $y$ 只包含 $1$ ，与上一种情况类似。
3. $y$ 中同时包含 $0$ 和 $1$ 。此时， $xyyz$ 中有一部分 $1$ 出现在了 $0$ 的前面，从而 $x{y}^{2}z\notin B$ ，矛盾。

因此 $B$ 不是正则的。

我们再证明 $C=\{w|count(0)=count(1)\}$ 不是正则语言。

假设 $C$ 是正则的。则 $C\cap 0^{\ast }{1}^{\ast }$ 也是正则的（并运算的封闭性）。然而 $C\cap 0^{\ast }{1}^{\ast }=B$ 不是正则的，因此 $C$ 不是正则的。

总之，使用泵引理去证明一个语言不是正则语言需要巧妙地选择 $s$ ，如果选取比较难的话，可以试着用另一个非正则语言去证明它。