【数据结构与算法分析——C语言描述】第九章:图论算法
【数据结构与算法分析——C语言描述】第九章:图论算法
标签(空格分隔):【数据结构与算法】
第九章:图论算法
- 第九章:图论算法
- 9.1 若干定义
- 9.1.1 图的表示
- 9.2 拓扑排序
- 9.3 最短路径算法
- 9.3.1 无权最短路径
- 9.3.2 Dijkstra算法
- 9.3.3 具有负边值的图
- 9.3.4 无圈图
- 补充:Huffman算法
- 我的微信公众号
- 9.1 若干定义
9.1 若干定义
- 一个图(graph) G=(V,E) G = ( V , E ) 由顶点(vertex) 集 V V 和 边(edge) 集 E E 组成。
- 每一条边就是一个 点对 (v,w) ( v , w ) , 其中 v,w∈V v , w ∈ V .有时候也把边叫做 弧(arc) .如果点对是有序的,那么图就是 有向的(directed) 或者 有向图(digraph).
- 顶点 v v 和 w w 邻接(adjacent)当且仅当 v,w∈E v , w ∈ E .在一个具有边 (v,w) ( v , w ) 从而具有 (w,v) ( w , v ) 的无向图中, v v 和 w w 邻接且 w w 和 v v 邻接。有时候还存在第三种成分,叫做 权(weight) 或者 值(cost).
- 路径(path):是一个顶点序列 w1,w2,...,wN w 1 , w 2 , . . . , w N ,使得 (wi,wi+1)∈E, 1≤i<N ( w i , w i + 1 ) ∈ E , 1 ≤ i < N 这样一条路径的 长(length)就这条路径上的边数,它等于 N−1 N − 1 .
- 定义特殊情形一种方便的方法:从一个顶点到它自身也可以看成一条路径;如果路径不包含边那么路径的长度为 0 0 .如果图含有一条从一个顶点到它自身的边 (v,v) ( v , v ) ,那么路径 v v 被称作环(loop).
- 简单路径:上面所有的顶点都是互异的,但是第一个顶点和最后一个顶点可能相同。
- 圈(cycle):有向图中的圈是满足 w1=wN w 1 = w N 且长度至少为 1 的一条路径。如果该路径是简单路径,那么这个圈就是简单圈。对于无向图而言,我们要求边是互异的。这种要求的根据在于无向图中的路径 u,v,u u , v , u 不应该被认为是圈,因为 (u,v),(v,u) ( u , v ) , ( v , u ) 是同一条边。但是在有向图中它们会被视为两种不同的边。如果一个有向图中不包含圈,那么就称它是无圈的(acyclic).一个有向无圈图简称为 DAG.
- 连通的(connected):如果在一个无向图中从每一个顶点到每一个其他顶点都存在一条路径,那么这个无向图便是连通的。具有这样的性质的有向图被称为 强连通的(strongly connected).
- 基础图(underlying graph):一个有向图的基础图是弧上去掉方向所形成的图。如果一个有向图的基础图是连通的,那么这个有向图被称为 弱连通的(weakly connected).
- 完全图(complete graph):每一对顶点都存在一条边的图.
9.1.1 图的表示
以有向图为例(无向图可以类似表示)
假设可以从 1 开始对定点进行编号,如下所示的图中,包含有 7 个顶点 和 12 条边。
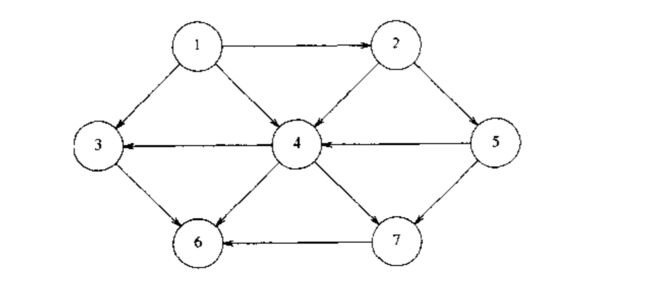
表示图的一种简单方法可以使用二维数组,称为 邻接矩阵(adjacency matric)表示法。对于每一条边 (u,v) ( u , v ) ,我们令 A[u][v]=1 A [ u ] [ v ] = 1 , 否则,数组的元素就是 0 .如果边有一个权,那么我们可以令 A[u][v] A [ u ] [ v ] 的值等于该权,而使用一个很大或者很小的标记表示不存在的边。
虽然这种表示方法十分简单,但是它的空间需求为 Θ(|V|2) Θ ( | V | 2 ) , 如果图的边不是很多,那么花费的代价是非常大的;如果或图是稠密的(dense), E=Θ(|V|2) E = Θ ( | V | 2 ) ,则邻接矩阵是一个非常好的选择。如果图是稀疏(sparse)的,更好的解决方法是使用邻接表(adjacency list),对于每一个顶点,我们使用一个表存放所有邻接的顶点。此时的空间需求是 O=(|V|+|E|) O = ( | V | + | E | ) .如果边有权,那么这个附加的信息也可以存储在单元中。

邻接表是表示图的标准方法。无向图可以类似地表示:每条边 (u,w) ( u , w ) 出现在两个表中,因此空间的使用基本上是双倍的。在图论算法中经常需要找出与某个给定的顶点 v v 邻接的所有的顶点。而这可以通过简单地扫描相应的邻接表来完成,所用时间与这些顶点的个数成正比。大部分实际应用中顶点都有名字而不是数字,这些名字在编译时都是未知的。由于我们不能通过未知名字为一个数组做索引,因此我们必须提供从名字到数字的映射。完成这项工作最容易的方法是使用散列表,在该散列表中我们对每个顶点储存一个名字以及一个范围在 1 1 到 |V| | V | 之间的内部编号。这些编号在图被读入时指定。指定的第一个数是 1 1 .在每条边被输入时,我们检查是否它的两个顶点都被指定了一个数,检查的方法是看是否顶点在散列表中。如果在,我们就是用这个内部编号;否则,我们将下一个可用的编号分配给该定点并把该顶点的名字和对应的编号插入散列表中。经过这样的变换,图论算法都将使用内部编号。由于最终我们还要输出顶点的名字而不是内部编号,因此对于每一个内部编号我们必须记录相应顶点的名字。一种记录方法是使用字符串数组。如果顶点名字过长,那么就会花费大量的空间。另一种是保留一个指向散列表内的指针数组,代价是稍微损失散列表ADT的纯洁性。
9.2 拓扑排序
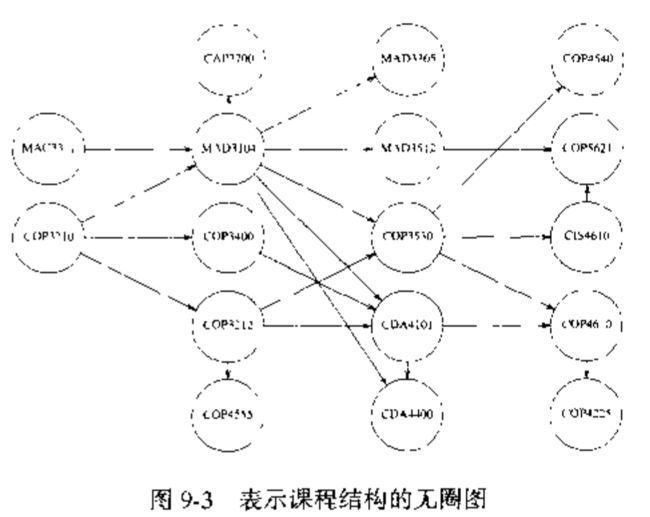
- 拓扑排序:是对有向无圈图的顶点的一种排序,它使得如果存在一条从 vi v i 到 vj v j 的路径,那么在排序中 vj v j 出现在 vi v i 的后面。如下图的课程结构,有向边 (v,w) ( v , w ) 表示课程 v v 必须在课程 w w 前修完。这些课程的拓扑排序不会破坏课程结构要求的任意课程序列。
- 如果图含有圈,那么拓扑排序是不可能的,因为对于圈上的两个顶点 v v 和 w w , v v 先于 w w , w w 又先于 v v .
此外,排序还不是唯一的,任何合理的排序都是可以的,对于下图, v1,v2,v5,v4,v3,v7,v6 v 1 , v 2 , v 5 , v 4 , v 3 , v 7 , v 6 和 v1,v2,v5,v4,v7,v3,v6 v 1 , v 2 , v 5 , v 4 , v 7 , v 3 , v 6 两个都是拓扑排序。
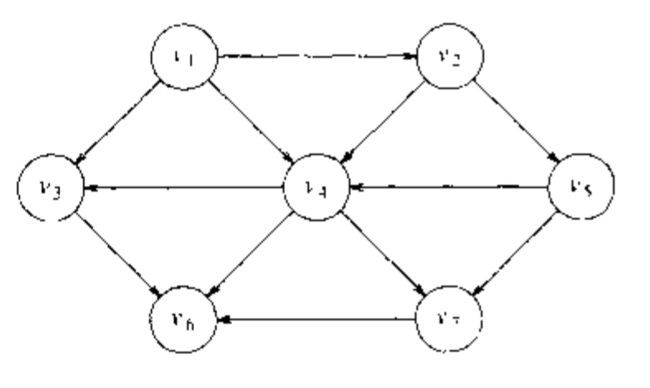
一个简单的求拓扑排序的算法是先找出任意一个没有入边的顶点。然后我们显示出该顶点,并将它和它的边从图中删除。然后,我们对图的其余部分应用同样的方法处理。
- 入度(indegree):顶点 v v 的入度为边 (u,v) ( u , v ) 的条数。
- 为了将上述方法形式化,我们计算图中所有顶点的入度。假设 Indegree 数组被初始化且图被读入一个邻接表中,则此时我们可应用下列算法生成一个拓扑排序.
//简单的拓扑排序伪代码
void Topsort( Graph G){
int Counter;
Vertex V,W;
for( Counter = 0; Counter < NumVertex; Counter++){
V = FindNewVertexOfIndegreeZero();
//FindNewVertexOfIndegreeZero函数扫描 Indegree 数组,寻找一个尚未被分配拓扑编号的入度为 0 的顶点。如果这样的顶点不存在,那么便返回 NotAVertex。这意味着该图有圈
if( V == NotAVerttex){
Error(" Graph has a cycle");
break;
}
TopNum[ V] = Counter;
for each W adjacent to V
Indegree[W]--;
}
}FindNewVertexOfIndegreeZero 是对 Indegree 数组的一个简单的顺序扫描,所以每次它的调用都花费 O(|V|) O ( | V | ) 时间,所以 V V 次调用花费的时间就是 O(|V|2) O ( | V | 2 )
- 改进的方法,上述算法运行时间长的原因在于 Indegress的顺序扫描。如果图是稀疏的,那么在每次迭代期间只有一些顶点的入度被更新。然而,虽然只有一小部分发生变化,但在搜索入度为 0 的顶点时我们查看了所有的顶点。我们可以通过将所有未被分配拓扑编号入度为 0 的顶点放在一个特殊的盒子中从而避免这种无效的劳动。此时 FindNewVertexOfIndegreeZero 函数返回并删除盒子中的任意顶点。当我们降低这些邻接顶点的入度时,检查每一个顶点并在它的入度将为 0 时把它放在盒子中。
- 如何实现这个盒子?可以使用一个栈或者队列。首先,对于每一个顶点计算它的入度。然后,将所有入度为 0 的顶点放入一个初始为空的队列中,当队列不空时,删除一个顶点 v v ,并将所有与 v v 邻接的顶点的入度减 1 .只要一个顶点的入度将为 0 ,就把该顶点放入队列中。此时,拓扑排序就是顶点处对的顺序。如下图:

void Topsort( Graph G){
Queue Q;
int Counter = 0;
Vertex V,W;
Q = CreatQueue( NuVertex);
MakeEmpty( Q);
for each vertex V
if( Indegree[V] == 0)
Enqueue( V,Q)
while( !IsEmpty(Q)){
V = Dequeue(Q);
TopNum[V] == ++Counter;
for each W adjacent to V
if( --Indegree[W] == 0)
Enqueue( W,Q);
}
if( Counter != NumVertex)
Error(" Graph has a clycle");
DisposeQueue( Q);
}如果使用邻接表,那么执行这个算法所需要的时间是 O(|E|+|V|) O ( | E | + | V | ) .
9.3 最短路径算法
- 输入是一个赋权图:与每条边 (vi,vj) ( v i , v j ) 相联系的是穿越该弧的值 ci,j c i , j .一条路径 v1,v2,...vN v 1 , v 2 , . . . v N 的值是 ∑N−1i=1ci,i+1 ∑ i = 1 N − 1 c i , i + 1 ,叫做赋权路径长(weighted path length),而无权路径长(unweighted path length)只是路径上的边数,即 N−1 N − 1 .
单源最短路径问题:
给定一个赋权图 G=(V,E) G = ( V , E ) 和一个特定点 s s 作为输入,找出从 s s 到 G G 中每一个其他顶点的最短赋权路径。例如:
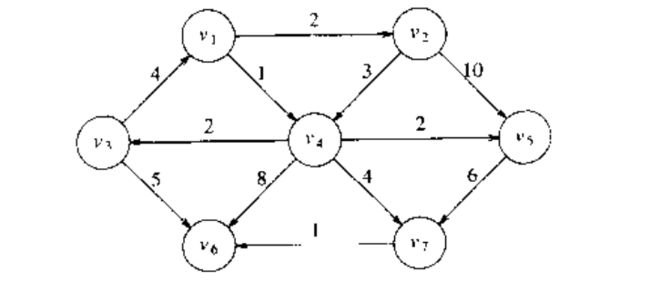
下图中,从 v1 v 1 到 v6 v 6 的最短赋权路径的值是 6 ,这条路径为 v1,v4,v7,v6 v 1 , v 4 , v 7 , v 6 .在两点间,最短的无权路径为 2 .一般而言,当我们不指明讨论的是赋权路径还是无权路径时,如果图是赋权的,那么路径就是赋权的。需要注意的是,在下图中,没有从 v6 v 6 到 v1 v 1 的路径。
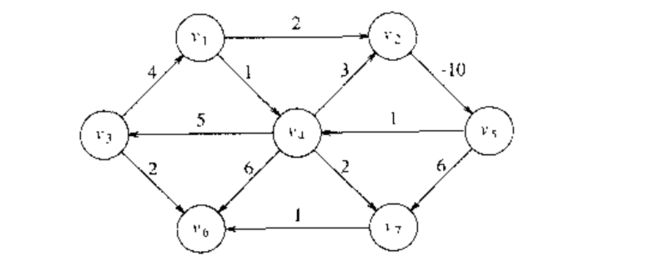
在下图中,我们考虑了存在负边的问题。从 v5 v 5 到 v4 v 4 的路径的值为 1 ,但是通过循环 v5,v4,v2,v5,v4 v 5 , v 4 , v 2 , v 5 , v 4 存在一条最短路径,它的值是 -5.这条路径不是最短的,因为我们可以在循环中滞留人一场。因此,在这两个顶点之间最短的路径是不能确定的。类似的,从 v1 v 1 到 v6 v 6 的最短路径也不是确定的,因为我们可以进入同样的循环。这个讯号被称作负值圈(negative-cost cycle),当它出现在图中时,最短路径问题无法确定。为方便起见,在没有负值圈时,从 s s 到 s s 的最短路径为 0.
我们将考虑解决问题四种形态的算法:
- 首先,我们考虑无权最短路径问题,并指出如何以 O(|E|+|V|) O ( | E | + | V | ) 时间解决它.
- 其次,假如没有负边,如何求解赋权最短路径问题。这个算法在使用合理的数据结构实现时的运行时间为 O(|E|log|V|) O ( | E | l o g | V | ) .
- 另外,如果图存在负边,我们将提供一个简单的解法,不过它的时间界不理想,为 O(|E|∗|V|) O ( | E | ∗ | V | ) .
- 最后,我们将以线性时间解决无圈图的特殊情况下的赋值的问题。
9.3.1 无权最短路径
- 广度优先搜索(breadth-first search)
下图表示一个无权的图 G G . 使用某个顶点 s s 作为输入参数,我们想要找出从 s s 到所有其他顶点的最短路径。我们只对包含在路径中的边数有兴趣,因此在边上不存在权。显然,这是赋权最短路径问题的特殊情形,我们可以令所有边的值为 1 .
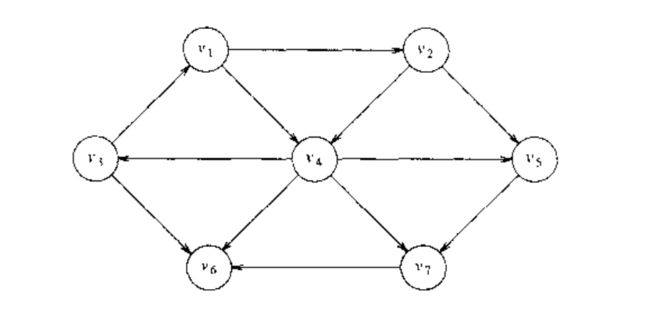
现在我们假设支队最短路径的长而不是具体路径感兴趣。记录实际的路径只不过是简单的记录问题。
设我们选择的 s s 为 v3 v 3 .此时立刻可以知道但从 s s 到 v3 v 3 的最短路径的长为 0 .把这个信息做标记,可以得到下图。
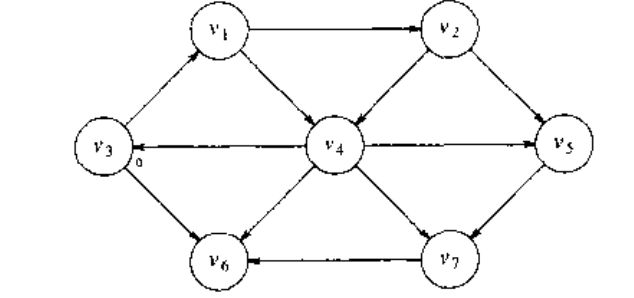
现在我们可以开始寻找所有与 s s 距离为 1 的顶点。这些顶点通过考察与 s s 邻接的那些顶点找到。此时我们看到, v1 v 1 和 v6 v 6 与 s s 只有一边之遥,我们可以把它们表示成下图。
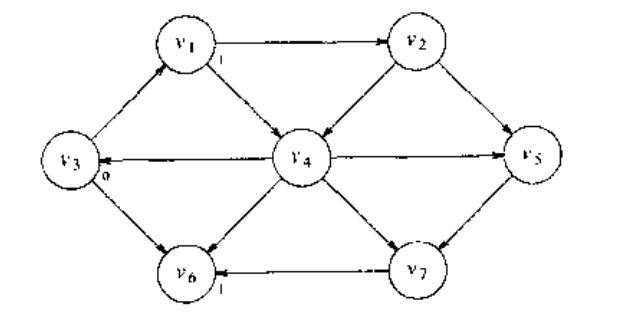
现在可以开始找出那些从 s s 出发最短路径恰好为 2 的顶点,我们找出所有邻接到 v1 v 1 和 v6 v 6 的顶点,它们的最短路径还不知道。这次搜索告诉我们,到 v2 v 2 和 v4 v 4 的最短路径长为 2.如下图:

最后,通过考察那些与刚被赋值的 v2 v 2 和 v4 v 4 相邻的顶点我们可以发现, v5 v 5 和 v7 v 7 各有一条三遍最短路径。现在苏素有的顶点都已经被计算,下图显示了算法最后的结果:
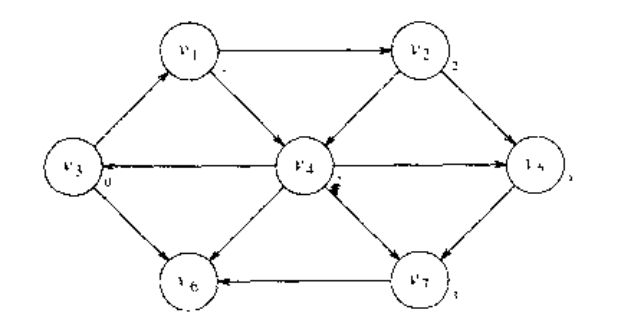
广度优先搜索方法按层处理顶点:距离开始点最近的那些顶点首先被赋值,距离最远的那些顶点最后被赋值。这与树的层次遍历很类似。
下图显示了该算法要用到的记录过程的表的初始配置:
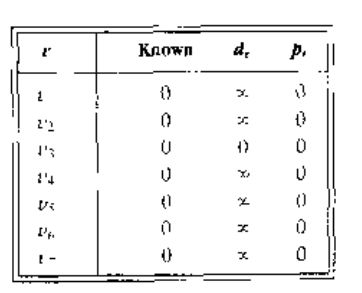
翻译成代码:对于每一个顶点,我们将跟踪三个信息。首先,我们把从 s s 开始到顶点的距离放到 dv d v 一栏中。开始的时候,除了 s s 之外的所有顶点都是不可到达的,而 s s 的路径长为 0 . Pv P v 一栏中的项为薄记变量,它将显示出实际的路径。 Known 一栏中的向在顶点被处理之后标记为 1 .起初,所有的顶点的 Known 标记都是为0,包括开始顶点,当一个顶点被标记为已知时,我们就确信不会再找到更便宜的路径,因此对该顶点的处理实质上已经完成。
基本的算法如下代码描述,这个算法模拟这些图表,它把距离 d=0 d = 0 上的顶点声明为 Known ,然后声明距离 d=1 d = 1 上的顶点声明为 Known , 等等,并且将 dw=∞ d w = ∞ 的所有邻接的顶点 w w 置为距离 dw=d+1 d w = d + 1 .之后追溯 Pv P v 变量,可以显示实际的路径.
//无权最短路径 广度优先
void Unweighted( Table T){
int CurrDist;
Vertex V,W;
for( CurrDist = 0; CurrDist for each vertex V
if( !T[V].Known && T[V].Dist == CurrDIst){
T[V].Known = True;
for each W adjacent to V
if( T[W].Dist == Infinity){
T[W].Dist = CurrDist + 1;
T[W].Path = V;
}
}
}
} 由于双层嵌套 for 循环,因此该算法运行时间为 O(|V|2) O ( | V | 2 ) .这个效率明显很低,因为尽管所有的顶点早就成 Known 了,但是外层的循环还是在继续,直到 NumVertex - 1 为止。虽然额外的附加测试避免了这种情况,但是最坏运行时间依旧如此,例如下图。

我们可以使用非常类似于对拓扑排序的做法来派出这一种低效性。在任一时刻,只要存在两种类型未知的顶点,它们的 dv≠∞ d v ≠ ∞ , 一些顶点的 dv=CurrDist d v = C u r r D i s t , 而其余的则有 dv=CurrDist+1 d v = C u r r D i s t + 1 .由于这种附加的结构,在第 2 行和第 3 行搜索整个的表以找出合适顶点的做法非常浪费。
一种非常简单但是抽象的解决方案是保留两个盒子。1#盒将装有 dv=CurrDist d v = C u r r D i s t , 而 2# 盒子中装有 dv=CurrDist+1 d v = C u r r D i s t + 1 个顶点。上述代码的测试中可以用查找 1# 盒内的任意顶点代替。在 if 语句之后,我们可以把 w w 加到 2# 盒中。在外层 for 循环中之以后,1# 盒是空的,而 2# 盒则可以转换成 1# 盒进行下一趟 for 循环。
精炼的算法如下,在下列伪代码中,我们假设已经开始顶点 s s 并且是直到的且 T[s].Dist T [ s ] . D i s t 为 0.
void Unweighted( Table T){
Queue Q;
Vertex V, W;
Q = CreatQueue( NumVertex);
MakeEmpty( Q);
Enqueue( S, Q);
while( !IsEmpty(Q)){
V = Dequeue( Q);
T[V].Knowm = True;
for each W adjacent to V
if( T[W].Dist == Infinity){
T[W].Dist = T[V].Dist + 1;
T[W].Path = V;
Enqueue( W,Q);
}
}
DisposeQueue( Q);
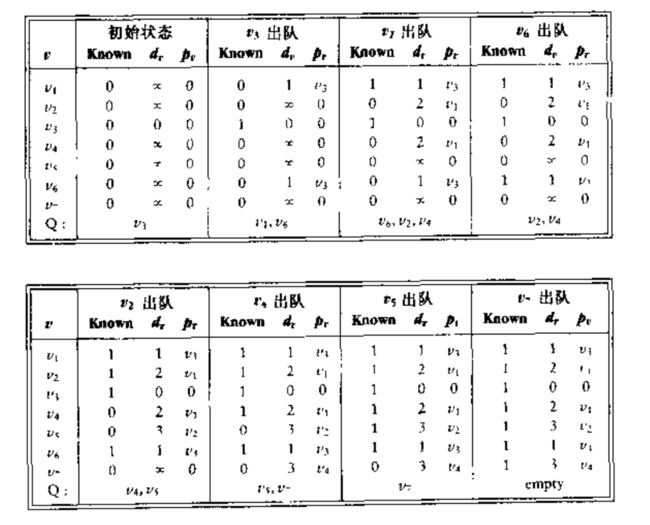
}9.3.2 Dijkstra算法
考虑图是赋权图得到情况。我们保留所有与前面相同的信息。因此,每个顶点或者标记为 Known 或者标记为 UnKnown.像以前一样,对于每一个顶点保留一个临时距离 dv d v ,这个距离实际上是使用已知顶点作为中间定点从 s s 到 v v 的最短路径长.和以前一样,我们记录 pv p v ,它是引起 dv d v 变化的最后的顶点。
- Dijkstra算法(Dijkstra’s algorithm):类似于无圈最短路径算法一样,按阶段执行。在每个阶段,Dijkstra算法选择一个顶点 v v ,它在所有未制顶点中具有最小的 dv d v ,同时算法声明从 s s 到 v v 的最短路径是已知的。阶段的其余部分由 dw d w 值得更新工作组成。
在无权的情况下,若 dw=∞ d w = ∞ 则置 dw=dv+1 d w = d v + 1 .因此,若顶点 v v 能提供一条更短路径,则我们本质上降低了 dw d w 的值。若果我们对于赋权的情形应用同样的逻辑,那么当 dw d w 的新的值应该是 dw=dv+Cv,w d w = d v + C v , w .简而言之,使用通向 w w 路径上的顶点 v v 是不是一个好主意由算法决定。原始的值 dw d w 是不用 v v 的值,上面算出来的值是使用 v v 最便宜的路径。
举个例子,如下图。
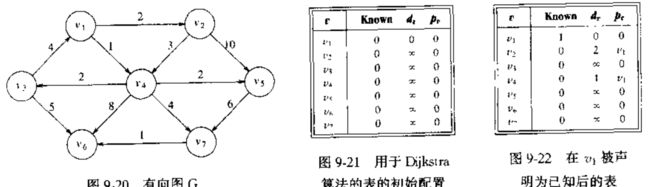
假设开始节点 s s 是 v1 v 1 .第一个选择的顶点是 v1 v 1 , 路径长为 0 ,该定点的标记为已知。既然 v1 v 1 已知,那么某些表项就需要调整,邻接 v1 v 1 的顶点是 v2 v 2 和 v4 v 4 .这两个顶点的项得到调整,便得到下图中最右侧一个表。
下一步,选择 v4 v 4 并标记为 Known,顶点 v3,v5,v6,v7 v 3 , v 5 , v 6 , v 7 都是邻接的顶点,而它们实际上都需要调整,如下图所示:

紧着是 v2 v 2 , v4 v 4 是邻接点,但是已经处于 Known 状态,因此对它无需改动。 v5 v 5 是邻接点,但是由于从 v2 v 2 经过到达 v5 v 5 的值为 10 + 2 = 12.而从 v4 v 4 经过的值为 3.因此不用改动。结果如下图:
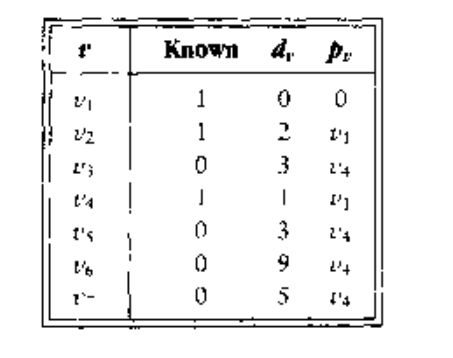
下一个被选择的顶点是 v5 v 5 ,其值为 3. v7 v 7 是唯一的邻接顶点,但是它不用调整,因为 3 + 6 > 5.
然后选择顶点 v3 v 3 ,对 v6 v 6 可以调整为 8.结果如下图:
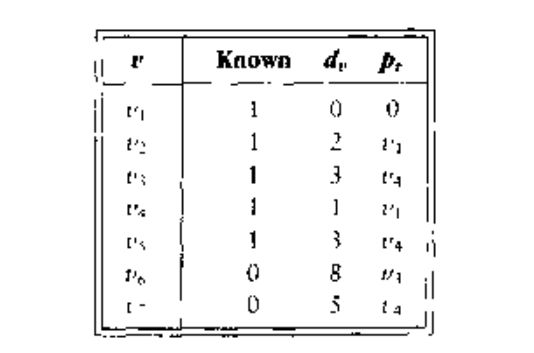
下一个选择的顶点是 v7 v 7 , v6 v 6 可以更改为6.最后选择的是 v6 v 6 .以上两步的表格如下:
为了显示出从开始定点到某个顶点 v v 的实际路径,我们可以编写一个递归程序跟踪 p p 数组留下的踪迹.
现在给出实现Dijkstra算法的伪代码,为了方便起见,我们假设这些顶点从 0 到 NumVertex - 1 标号,并假设通过例程 ReadGraph 我们的图可以被读入到一个邻接表中。
//有权路径的Dijkstra算法
typedef in Vertex;
struct TableEntry{
List Header;
int Known;
DistType Dist;
Vertex Path;
};
#difine NotAVertex (-1)
typedef struct TableEntry Table[ NumVertex];
void InitTable( Vertex Start, Graph G, Table T){
int i;
ReadGraph( G,T)
for( i = 0; i< NumVerttex; i++){
T[i].Known = False;
T[i].Dist = Infinity;
T[i].Path = NotAVertex;
}
T[Start].dist = 0;
}
void PrintPath( Vertex V, Table T){
if( T[V].Path != NotAVertex){
PrintPath( T[V].Path, T);
printf(" to");
}
printf("%v", V);
}
void Dijkstra( Table T){
Vertex V, W;
for( ;;){
V = smallest unknown distance Vertex;
if( V == NotAVetex)
break;
T[V].Known = True;
for each W adjacent to V
if( !T[W].Known)
if( T[V].Dist + Cvw < T[W].Dist){
Decrease( T[W].Dist to T[V].Dist + Cvw);
T[W].Path = V;
}
}
}9.3.3 具有负边值的图
如果图具有负边值,那么Dijkstra算法算法是行不通的,原因在于,一旦一个顶点 u u 被声明是已知的。那么就有可能从另外的某个位置顶点 v v 到 u u 的负的路径。在
- 一个方案是在各边的值上增加一个常数 Δ Δ ,如此一来,除去了负值边。可是这种方案不可能直接实现,因为那些具有许多条边的路径变得比那些具有很少边的路径权重更重了。
9.3.4 无圈图
补充:Huffman算法
- 哈夫曼算法可以描述如下:算法对一棵由树组成的森林进行,一棵树的权等于它的树叶的频率的和,我们假设字符的个数为 C , 任意选取最小权的两棵树 T1 T 1 和 T2 T 2 为子树的新树,这样的过程进行 C - 1 次。在算法的开始,存在 C 棵单节点数——每个字符一棵。在算法结束时得到一棵树,这棵树就是最优哈夫曼编码码树。
- 我们通过一个例子来理解这个算法的操作。
如下图,表示的初始的森林,每棵树的权在根处以小号的数字表示。
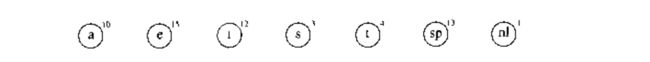
将两棵权重最低的树合并在一起,得到森林如下图:

我们将新的根命名为 T1 T 1 ,这样便可以准确无误地表述下一步合并。我们令 s s 左儿子,注意,哈夫曼算法描述具有任意性, s s 是左儿子右儿子是任意的。新树的总的权等于老树的权重的和。
之后再选择两权中最小的树,这两棵树分别是 T1 T 1 和 t t ,然后将它们合并成一棵新的树,如下图,树根为 T2 T 2 ,权重为 8 .
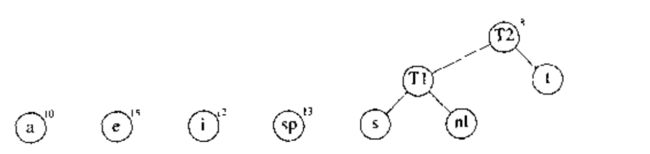
第三步骤合并 T2 T 2 和 a a 建立 T3 T 3 ,其权重为 10 + 8 = 18.
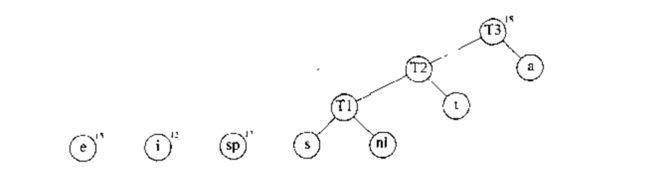
接下来合并 i i 和 sp s p 建立 T4 T 4 .
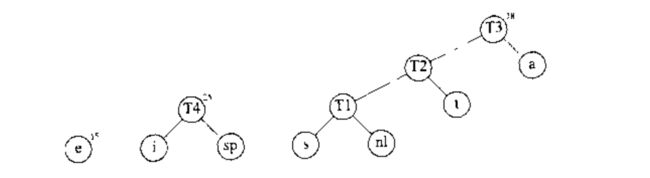
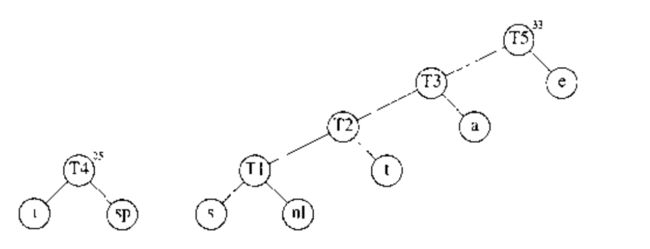
然后合并 e e 和 T3 T 3 建立 T5 T 5 ,最后将剩下两课树合并成 T6 T 6 最优树.

我的微信公众号
![]()