机器学习实战之SVD
1. 奇异值分解 SVD(singular value decomposition)
1.1 SVD评价
优点: 简化数据, 去除噪声和冗余信息, 提高算法的结果
缺点: 数据的转换可能难以理解
1.2 SVD应用
(1) 隐性语义索引(latent semantic indexing, LSI)/隐性语义分析(latent semantic analysis, LSA)
在LSI中, 一个矩阵由文档和词语组成的.在该矩阵上应用SVD可以构建多个奇异值, 这些奇异值代表文档中的概念或主题, 可以用于更高效的文档搜索.
(2) 推荐系统
先利用SVD从数据中构建一个主题空间, 然后在该主题空间下计算相似度.
1.3 SVD分解
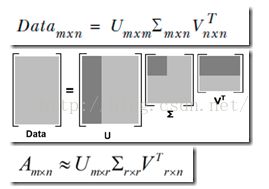
SVD是一种矩阵分解技术,其将原始的数据集矩阵A(m*n)分解为三个矩阵, ![]() ,分解得到的三个矩阵的维度分别为m*m,m*n,n*n.其中
,分解得到的三个矩阵的维度分别为m*m,m*n,n*n.其中![]() 除了对角元素不为0,其它元素均为0,其对角元素称为奇异值,且按从大到小的顺序排列, 这些奇异值对应原始数据集矩阵A的奇异值,即A*A(T)的特征值的平方根.
除了对角元素不为0,其它元素均为0,其对角元素称为奇异值,且按从大到小的顺序排列, 这些奇异值对应原始数据集矩阵A的奇异值,即A*A(T)的特征值的平方根.
在某个奇异值(r个)之后, 其它的奇异值由于值太小,被忽略置为0, 这就意味着数据集中仅有r个重要特征,而其余特征都是噪声或冗余特征.如下图所示:
问题: 如何选择数值r?
解答: 确定要保留的奇异值数目有很多启发式的策略,其中一个典型的做法就是保留矩阵中90%的能量信息.为了计算能量信息,将所有的奇异值求其平方和,从大到小叠加奇异值,直到奇异值之和达到总值的90%为止;另一种方法是,当矩阵有上万个奇异值时, 直接保留前2000或3000个.,但是后一种方法不能保证前3000个奇异值能够包含钱90%的能量信息,但是操作简单.
****SVD分解很耗时,通过离线方式计算SVD分解和相似度计算,是一种减少冗余计算和推荐所需时间的办法.
2. 基于协同过滤的推荐引擎
2.1 定义
协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的.
例如: 试图对某个用户喜欢的电影进行预测,搜索引擎会发现有一部电影该用户还没看过,然后它会计算该电影和用户看过的电影之间的相似度, 如果相似度很高, 推荐算法就会认为用户喜欢这部电影.
缺点: 在协同过滤情况下, 由于新物品到来时由于缺乏所有用户对其的喜好信息,因此无法判断每个用户对其的喜好.而无法判断某个用户对其的喜好,也就无法利用该商品.
2.2 相似度计算
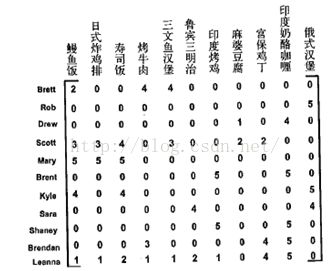
协同过滤利用用户对食物的意见来计算相似度,下图给出了一些用户对菜的评级信息所组成的矩阵:
定义相似度在0-1之间变化,且物品对越相似,其相似度值越大,可以使用公式 相似度 = 1/(1 + 距离) 来计算相似度.
计算距离的方法如下:
(1) 欧氏距离
(2)皮尔逊相关系数(pearson correlation)
度量两个向量间的相似度,该方法优于欧氏在于其对用户评级的量级不敏感,例如某个人对所有物品的评分都是5分,另一个人对所有物品评分都是1分,皮尔逊相关系数认为这两个评分向量是相等的. 不过皮尔逊相关系数的取值范围是(-1,1),通过0.5 + 0.5 * corrcoef()将其归一化到0-1之间.
(3) 余弦相似度( cosine similarity)
计算的是两个向量夹角的余弦值.其取值范围是(-1,1),因此也要将其归一化到(0,1)区间.
以下是这三种相似度计算方法的代码实现:
def eulidSim(in1,in2):
return 1.0/(1.0+la.norm(in1-in2))
def pearsonSim(in1,in2):
if len(in1) < 3: #检查是否存在3个或更多的点,小于的话,这两个向量完全相关
return 1.0
return 0.5 + 0.5 * corrcoef(in1,in2,rowvar = 0)[0][1]
def cosSim(in1,in2):
num = float(in1.T * in2)
denom = la.norm(in1) * la.norm(in2)
return 0.5 + 0.5 * (num/denom)
(1) 用处: 推荐餐馆食物. 给定一个用户, 系统会为此用户推荐N个最好的推荐菜.为了实现这一目的,要做到:
- 寻找用户没有评级的菜, 即在用户-物品矩阵中的0值;
- 在用户没有评级的所有物品中,对每个物品预计一个可能的评级分数.
- 对这些物品的评分从高到低进行排序,返回前n个物品
下面是实现代码:
#计算在给定相似度计算方法的条件下,用户user对物品item的估计评分值
def standEst(dataMat,user,simMea,item):
n = shape(dataMat)[1]
simTotal = 0.0
ratSimTotal = 0.0
for j in range(n):
userRate = dataMat[user,j]
if userRate == 0 :
continue
#得到对菜item和j都评过分的用户id,用来计算物品item和j之间的相似度
overlap = nonzero(logical_and(dataMat[:,item].A>0,dataMat[:,j].A>0))[0]
if len(overlap) == 0:
similarity = 0
else:
#计算物品item和j之间的相似度(必须选取用户对这两个物品都评分的用户分数构成物品分数向量)
similarity = simMea(dataMat[overlap,item],dataMat[overlap,j])
simTotal += similarity
ratSimTotal += similarity * userRate
if simTotal ==0:
return 0
else:
return ratSimTotal/simTotal #归一化处理
#输入依次是数据矩阵,用户编号,返回的菜的个数,距离计算方法,获得物品评分的函数
def recommend(dataMat,user,n=3,simMea=cosSim,estMethod=standEst):
#返回user用户未评分的菜的下标
unratedItem = nonzero(dataMat[user,:].A == 0)[1]
if(len(unratedItem) == 0):
return 'you rated every one'
itemScore = []
#对每个没评分的菜都估计该用户可能赋予的分数
for item in unratedItem:
score = estMethod(dataMat,user,simMea,item)
itemScore.append((item,score))
#返回评分最高的前n个菜下标以及分数
return sorted(itemScore, key = lambda jj:jj[1],reverse = True)[:n]实际的数据集得到的矩阵相当稀疏,因此可以先利用SVD将原始矩阵映射到低维空间中,; 然后再在低维空间中, 计算物品间的相似度,大大减少计算量.
其代码实现如下:
#通过SVD对原始数据矩阵降维,便于计算物品间的相似度
def scdEst(dataMat,user,simMea,item):
n = shape(dataMat)[1]
simTotal = 0.0
ratSimTotal = 0.0
u,sigma,vt = la.svd(dataMat) #sigma是行向量
sig4 = mat(eye(4) * sigma[:4]) #只利用最大的4个奇异值,将其转换为4*4矩阵,非对角元素为0
xformedItems = dataMat.T * u[:,:4] * sig4.I #得到n*4
for j in range(n):
userRate = dataMat[user,j]
if userRate == 0 or j == item:
continue
#得到对菜item和j都评过分的用户id,用来计算物品item和j之间的相似度
#overlap = nonzero(logical_and(dataMat[:,item].A>0,dataMat[:,j].A>0))[0]
#if len(overlap) == 0:
# similarity = 0
#else:
#计算物品item和j之间的相似度
# similarity = simMea(dataMat[overlap,item],dataMat[overlap,j])
similarity = simMea(xformedItems[item,:].T,xformedItems[j,:].T)
simTotal += similarity
ratSimTotal += similarity * userRate
if simTotal ==0:
return 0
else:
return ratSimTotal/simTotal #归一化处理#打印矩阵
def printMat(in1,thresh=0.8):
for i in range(32):
for k in range(32):
if(float(in1[i,k]) > thresh):
print 1,
else:
print 0,
print ''
#利用SVD实现图像压缩,允许基于任意给定的奇异值来重构图像,默认去前3个奇异值
def imgCompress(numSV=3,thresh=0.8):
#32*32 matrix
my1 = []
for line in open('0_5.txt').readlines():
newrow = []
for i in range(32):
newrow.append(int(line[i]))
my1.append(newrow)
myMat = mat(my1)
print '***original matrix***'
printMat(myMat)
u,sigma,vt = la.svd(myMat)
#将sigma矩阵化,即sigrecon的对角元素是sigma的元素
sigrecon = mat(zeros((numSV,numSV)))
for k in range(numSV):
sigrecon[k,k] = sigma[k]
#重构矩阵
reconMat = u[:,:numSV] * sigrecon * vt[:numSV,:]
print '***reconstruct matrix***'
printMat(reconMat)以数字为例:数字0存储为32*32的矩阵,需要存储1024个数据; 通过实验发现只需要2个奇异值就能够很精确地对图像进行重构,u,vt的大小都是32*2的矩阵,再加上2个奇异值,则需要32*2*2+2=130个0-1值来存储0;通过对比发现,实现了几乎10倍的压缩比.