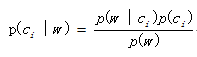朴素贝叶斯分类器算法通俗讲解
首先会用到贝叶斯决策理论,说一下。贝叶斯决策理论的核心思想是:选择具有最高概率的决策。例如一个点(x, y),属于类别1的概率是p1(x, y),属于类别2的概率是p2(x, y),用贝叶斯决策理论来判断它的类别:
如果p1(x, y) > p2(x, y),那么类别1;
如果p1(x, y) < p2(x, y),那么类别2。
再说一下条件概率。计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即已经p(x|c),计算p(c|x),利用好求的概率去求解难求的概率。计算公式:
接下来我们讨论如何结合贝叶斯决策理论使用条件概率将其应用到分类器中。
我们需要比较的是p(c1 | x, y) 和p(c2 | x, y),即(x,y)表示的数据点属于类别c1和c2的概率各是多少?直接求解这两个概率不好求解,我们利用贝叶斯准则来交换概率中条件和结果,具体的用到下面公式:
利用已知的三个概率值来求解未知的概率值。
再来说一下标题中的朴素贝叶斯,为什么叫做“朴素”。朴素贝叶斯是贝叶斯分类器的一个扩展,是用于文档分类的常用算法。朴素贝叶斯有两个假设:(1)一个特征或单词出现的可能性与它和其他单词相邻没有关系,特征间相互独立,正是“朴素”之含义;(2)每个特征同等重要。其实这两个假设都有点问题:(1)比如单词bacon出现在delicious附件多,出现在unhealthy附近少;(2)比如判断留言板的留言是否得当,可能不需要看完所有的1000个词,只需看20个左右的词就足以判断了。尽管朴素贝叶斯的上述两个假设存在一些小的瑕疵,但是朴素贝叶斯的实际效果却很好。我们称之为“朴素”,是因为整个形式化过程只做最原始、最简单的假设。
下面看一个例子简单说明具体过程。
对留言板的留言进行分类(侮辱性和非侮辱性)
- 首先将每条留言转换为词条列表listOPosts,并且每条留言有类别标签listClasses,1表示侮辱性,0表示非侮辱性。
listOPosts = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
listClasses = [0, 1, 0, 1, 0, 1]
2. 获取词汇表myVocabList,将所有出现的不重复的单词列入其中。
myVocabList=['cute', 'love', 'help', 'garbage', 'quit', 'I', 'problems', 'is', 'park', 'stop', 'flea', 'dalmation', 'licks', 'food', 'not', 'him', 'buying', 'posting', 'has', 'worthless', 'ate', 'to', 'maybe', 'please', 'dog', 'how', 'stupid', 'so', 'take', 'mr', 'steak', 'my']
3. 将留言的词条列表通过词汇表转换为词条向量,长度与词汇表长度相同,依次检查,词条出现在文档中记作1,未出现在文档中的记作0。例如listOPosts中的第一条留言转换为词条向量为:
[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1]
4. 利用朴素贝叶斯准则计算公式中的概率值。
将(x, y)替换为w(代表向量,由多个数值组成,此处个数等于词条向量长度)
P(ci)容易求出,每个留言有类别标签。此处p(c1)=0.5,p(c2)=0.5。
由于朴素贝叶斯假设每个特征独立,所以:
p(w|ci)=p(w1, w2, w3, ……wn|ci)=p(w1|ci)(w2|ci)p(w3|ci)……p(wn|ci)
现在就要求出每个p(wi|ci)
5. 贝叶斯分类器训练函数
求p(wi|ci)。对于类别1,将所有属于类别1的词条向量直接相加(都是有1和0数字组成),就能算出类别1中每个词条出现多少次,除以类别1的总词条个数,就能求出类别1中每个词条出现的概率。同理求出类别0的每个词条出现的概率。这就是朴素贝叶斯分类器训练函数。最后输出结果为类别0的词条概率向量p0Vect、类别1的词条概率向量p1Vect、侮辱性类别1的概率pAbusive,即:
p0Vect=[0.04166667 0.04166667 0.04166667 0. 0. 0.04166667 0.04166667 0.04166667 0. 0.04166667 0.04166667 0.04166667 0.04166667 0. 0. 0.08333333 0. 0. 0.04166667 0. 0.04166667 0.04166667 0. 0.04166667 0.04166667 0.04166667 0. 0.04166667 0. 0.04166667 0.04166667 0.125 ]
p1Vect=[形式同上]
pAbusive=0.5
6. 至此,公式右边的分子部分我们都可以求出来了,至于分母对于类别1和类别0是相等的(常量),不随类别1和类别0而变化,因此可以省去,直接根据分子比较就能比较出w属于类别1还是类别0。
7. 朴素贝叶斯分类函数。直接根据已知概率可以比较概率了,所以
如果p(c1 |w) > p(c0 | w),属于类别1
如果p(c1 |w) < p(c0 | w),属于类别0
8. 测试。可以根据分类函数将数据集分类成训练集和测试集,通过正确率(测试集中正确分类占总数比例)来检验算法性能。可以修改分类器,比如初始化向量时的值,比如求积时取对数等。在此不做解释了,代码里有变更。
至此朴素贝叶斯分类器算法的基本概率、基本流程、基本应用已结介绍完,朴素贝叶斯分类器算法的代码(包含实例:垃圾邮件过滤)见https://download.csdn.net/download/u012494321/10781825。