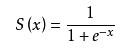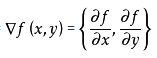Logistic回归算法讲解

         回归：假设有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。

Logistic回归进行分类是根据现有数据对分类边界线建立回归公式（找最佳拟合），以此进行分类。这里的回归表示要找到最佳拟合参数集，多元函数的参数集合，非线性回归。

         Logistic回归训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。不同于之前的分类算法为寻找最优只是调整参数大小，这里用到了寻找最优的算法。

知识回顾：

1.导数是针对一元函数求导，几何意义是（在某点的）切线斜率。

2.偏导数是针对多元函数，求沿某一个坐标轴正方向（一元方向）的变化率。

3.梯度也是针对多元函数，是所有方向上的偏导数组成的向量，其几何意义是在曲面上的某一点增加（减少）最快的方向，可沿该方向（不断更新）求函数的最大值（最小值）。

4.方向导数与梯度不同，是沿着某个方向（多元方向）的变化率。

（一）基于Logistic回归和Sigmoid函数的分类

（1）Sigmoid函数

        该分类器适合解决二分类问题，类别输出为1和0，有这样的函数，称为海维赛德阶跃函数，或称单位阶跃函数。但是这种瞬间跳跃过程有时候难处理。幸好，有另一个函数Sigmoid函数，值域为（0,1），公式如下：

        函数图像如下：

        当x=0时，S(x)=0.5

        当x>0时，S(x)>0.5

        当x<0时，S(x)<0.5

（2）分类器

        为了实现Logistic回归分类器，我们将分类器的所有输入值（样本特征值）分别乘以一个回归系数，再将相乘结果相加，得到的值代入S(x)函数里，

        如果S(x)>0.5时归类为1，

        如果S(x)>=0.5时归类为0，

        这就是分类器的思路方法。

        下面该讨论回归系数怎么确定了。

二、基于最优化方法的最佳回归系数确定

        Sigmoid函数的输入记为z，

        z=w0x0+w1x1+……wnxn

        x0, x1,…… xn是特征值，w0 , w1……wn是需要确定的权重系数，即我们需要通过最优化算法求出这些系数。

（1）梯度上升法

        算法思想：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。函数f(x, y)的梯度表示为：

        

        梯度沿x方向移动，沿y方向移动，梯度总是沿着函数值增长最快的方向。梯度上升算法到达每个点后会重新估计移动方向。移动量的大小用步长α表示。用向量表示的话（w代表特征值向量），梯度上升算法的迭代公式如下：

        w : = w + α▽f (x)

        此处省略了数学推导，定性地说，这里是在计算真实类别与预测类别的差值，迭代过程就是按照该差值的方向调整回归系数。

        该公式一直被迭代执行，直到达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

        梯度上升算每次更新回归系数时都需要遍历整个数据集，数据集小的时候尚可，但是如果有数十亿样本和成千上万的特征时，虽然分类精确度很好，该方法的计算复杂度就太高了。所以引出了随机提到上升算法。

（2）随机梯度上升算法

        基本思想：每次更新回归系数仅用一个样本点来更新，迭代的次数就是样本数量。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应，一次处理所有数据被称作“批处理”。

        随机梯度上升算法在效果上表现的没有梯度算法那么完美。

        还有一个问题就是，某些回归系数可能需要经过很多次迭代才能达到稳定值，另外，在大的波动停止后，还有一些小的周期性波动。产生这种现象的原因是存在一些不能正确分类的样本点（数据集并非线性可分），在每次迭代时会引发系数的剧烈改变。我们期望算法能够避免来回波动，从而收敛到某个值。另外收敛速度也需要加快。这里又引出改进的随机梯度上升算法。

（3）改进的随机梯度上升算法

        改进处有两点：第一，alpha在每次迭代时都会调整，一方面缓解数据波动或高频波动，另一方面保证在多次迭代之后新数据仍然具有一定的影响。第二，通过随机选取样本来更新回归系数，减少周期性的波动，而不是挨着顺序依次取样本。具体做法是：每次随机从列表中选取一个样本值，然后从列表中删除掉该值再进行下一次迭代。第三，增加了一个迭代次数作为参数，使迭代次数适当增加（非样本数量次数，而是倍数），使回归系数更加精准。

 

资源链接地址：https://download.csdn.net/download/u012494321/10814124