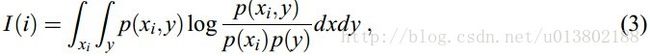特征选择(Feature Selection)
交叉验证
直接介绍k折叠交叉验证(k-fold cross validation):
1. 特征选择
1.1 相关系数
先考虑对连续的输出y进行预测,皮尔森相关性系数为:
Cov代表协方差,var代表方差,R(i)的估计定义为:
相关性系数描述了xi与y之间的相关性,如果R(i)等于1或者-1,则xi与y线性相关。所以,我们可以用![]() 作为特征排列的一个评判标准。
作为特征排列的一个评判标准。
1.2 信息论排列规则
依赖于不同变量与目标之间的互信息的估计:
I(i)是用来衡量变量xi的密度与目标y的密度的依赖。而问题在于P(xi),P(y)和P(xi,y)都是未知的,并且难以从数据中估计。离散的变量通常是最简单的,可以用频率估计概率,将积分转化为求和:
1.3 那么一个冗余变量的子集有没有可能对模型的性能造成影响呢?
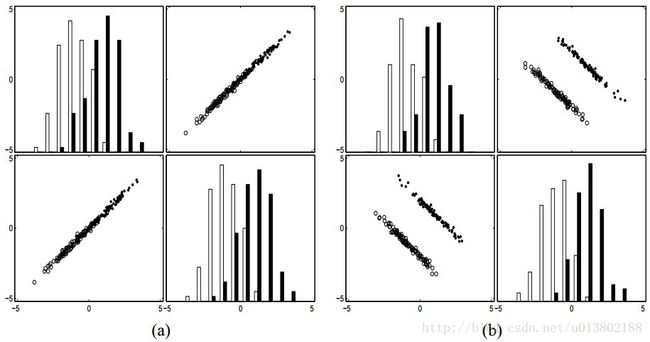
上图表述了从可能的冗余变量中获得的信息。A代表了一个具有独立同分布变量的二类问题,每一类都有一个协方差为0的高斯分布。B,对同样的问题进行45°的旋转,两个变量联合出现了一个根号2的提升,所以独立同分布并不是真正冗余的。
通过平均n个独立同分布的随机变量,我们可以得到一个根号n的标准偏差的下降。
通过添加可能是多余的变量可能会减少噪声,使分类的性能更好。
1.4 相关性怎么作用于变量的冗余?
上图描述了内部类的协方差。轴线上的投影,两个变量的分布跟之前的例子一样。A代表类的条件分布在两个类的中心的那条线的方向上有一个高的协方差,所以用两个变量相比于一个变量来说对分类没什么意义。B代表类的条件分布在两个类的中心的垂直方向上有很高的协方差,用两个变量就比一个变量获得一个很好的分类了。所以完全的相关变量是真的冗余的,那就意味着添加他们不会获得额外的信息。然而,非常高的相关性并不意味着变量互补性的缺失。
1.5 有没有可能,一个变量单独是没有用的,跟其他变量一起就是有用的呢?
多变量的方法有一个显著的问题,就是有过拟合的倾向。
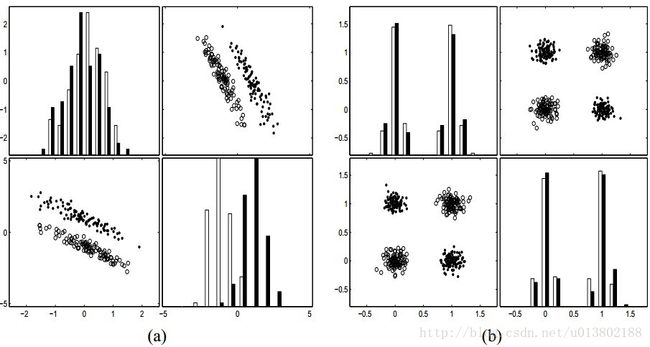
上图中的a,两个类条件分布拥有相同的协方差矩阵,主要的方向是面向对角的。
类的中心在一条轴线上被分隔开,而没有被另一条轴线分隔开,一个变量本身是没有用的,二维的分割方式却比使用单一的有用的变量要好。所以,我们提出的问题时会发生的。那么下一个问题是:如果两个变量本身都是没有用的,那么他们合起来会有用吗?在b中,四个中心(0; 0), (0; 1), (1; 0), 和 (1; 1),单一的使用哪一个变量都不可分,但是他们二维可分。所以,即使两个没有用的变量,合起来也可以是有用的。
2. 变量子集的选择
这个问题有三种解决方案:封装,过滤,嵌入(wrappers, filters, and embedded methods)。
封装像是一个黑盒根据他们的预测能力对变量的子集进行评分。过滤器选择变量的子集为一种预处理的步骤,独立于预报器的选择(predictor)。嵌入方法在训练进程上比较特殊。
2.1 封装和嵌入
封装的思想包括使用一个给定模型的预测性能来评估变量子集的关联用处。实际上,我们需要定义:(1)怎么去寻找所有可能的变量子集空间。(2)怎么去评估一个模型的性能.(3)使用哪一种预测器(predictor)。如果可能性不是很多的话,可以用穷举法,当然只是一个NP-hard 问题(Amaldi and Kann, 1998)。当然也可以采用一些策略,例如最佳优先(best-first),分支界定(branch-and-bound),模拟退火(simulated annealing,),遗传算法(geneticalgorithms)(Kohavi and John, 1997)。性能评估可以用交叉验证来做。通用的预测器有决策树,朴素贝叶斯,最小二乘,支持向量机。封装被人诟病的一点是它有点像是暴力解法,需要大量的甚至不必要的计算。贪心法通常是用来提高有利的计算,并避免过拟合的。有两种表述:前向选择(forward selection)和后向淘汰(backward elimination)。前向选取(Forward Selection),首先,初始化特征子集F为空集,然后对不属于F的特征,计算添加该特征之后模型提升的精度,选取其中提升精度最大的特征添加到F中,循环以上操作直至精度不再提升。后向淘汰(Backward Elimination),与前向选择相反,后向淘汰将F初始化为所有特征的集合,每次选取一个特征,计算不考虑该特征的时候模型的精度,若精度提升,则将该特征剔除F,直至精度不再下降。这两种算法都会产生变量的嵌套子集。而嵌入法现在有:决策树CART,拥有一个内建的机制去展现变量的选择。
2.2 嵌套子集方法
令s为某一步算法所选择的变量的数量,J(s)使用这一个变量子集的目标函数。我们来预测目标函数的变化:
(1) 有限的差分计算:计算J(s) 与 J(s + 1) 或 J(s − 1)的差值。
(2) 代价函数的二次逼近:在后向淘汰中,通过修剪输入参数的权重wi,可以得到二阶的泰勒展开式。在最优化J的过程中,一阶项可以被忽略,得到参数i通过
(3) 目标函数的灵敏度计算:用J导数的绝对值或者二次方表示。
2.3 直接目标优化
(1) 最大化拟合优度
(2) 最小化变量数量
所以这种方法包括两部分目标函数,最好的例子是SVM。其实没有哪种方法能直接减少变量数量,但有些方法可以削减变量的规模。
2.4 过滤器
经论证,相比于封装,过滤器要更快。当然,最近证明高效的嵌入式方法在这方面也是有竞争力的。同时,过滤器也可以用于降维和克服过拟合。基于信息论的过滤算法有马尔科夫覆盖算法(Markov blanket)。
3. 特征构造与空间降维
3.1 聚类(Clustering)
基本思想是将一组相似的变量替换成聚类中心,然后变成一个特征。其中比较代表性的有K-means 和 hierarchical clustering。分布聚类(Distributionalclustering)是基于信息瓶颈理论(information bottleneck (IB) theory),定义![]() 为代表构造特征的随机变量,IB方法将会寻找最小化的互信息
为代表构造特征的随机变量,IB方法将会寻找最小化的互信息![]() ,保留互信息
,保留互信息![]() ,通过构造拉格朗日算子
,通过构造拉格朗日算子![]() 来建立全局的目标函数。另外,可以对代表文本类别频率计数的向量使用k-means聚类。相似度度量是使用K-L散度,也就是相对熵
来建立全局的目标函数。另外,可以对代表文本类别频率计数的向量使用k-means聚类。相似度度量是使用K-L散度,也就是相对熵![]()
3.2 矩阵因子分解
特征构造的另一个广泛的应用是奇异值分解(singular value decomposition).SVD的目标是构建原始变量的线性组合的一系列特征,也是最小二乘思想上原始数据重构的最可能的方法。在Globerson and Tishby (2003)的论文中展现了一个无监督的构造 方法:sufficientdimensionality reduction,是一种在数据重构和数据压缩之间的权衡。特征被构造成目标优化的拉格朗日算子,mxn维的非负矩阵P代表了两个随机变量的联合分布。![]() ,对d特征的集合,Φ是一个mx(d+2)的矩阵,其d+1列是1,Ψ是一个(d+2)xn的矩阵,其d+2列是1,Z是一个归一化的参数。
,对d特征的集合,Φ是一个mx(d+2)的矩阵,其d+1列是1,Ψ是一个(d+2)xn的矩阵,其d+2列是1,Z是一个归一化的参数。