《图像处理、分析与机器视觉 第四版》图像分析的数据结构——学习笔记
文章目录
- 图像数据表示的层次
- 传统图像数据结构
- 矩阵
- 共生矩阵
- 积分图像
- 链
- 拓扑数据结构
- 关系结构
- 分层数据结构
- 金字塔
- 四叉树
数据和算法是任何程序的两个核心部分。数据的组织通常在很大程度上影响着算法的选择和实现的简洁性, 因此,在写程序时数据结构的选择是一个重要问题。
首先处理在图像分析任务中的信息表示的基本层次, 然后来讨论传统的数据结构, 包括矩阵、 链、 关系结构。 最后我们要考虑分层数据结构, 如金字塔和四叉树。
图像数据表示的层次
计算机视觉感知的目的是寻找输入图像与真实世界之间的关系。计算机视觉由如下的设计所组成:
- 中间表示(数据结构)
- 创建这些中间表示所用的算法和他们之间的关系导入
这些表示可以分为四个层次,但是,它们之间并没有严格的界限。
- 第一层:图标图像。由含有原始数据的图像组成, 原始数据也就是像素亮度数据的整数矩阵。 为了突出对后续处理重要的图像的某些方面,需要进行预处理,这个过程的输出图像也是这个层次的。
- 第二层:分割图像。图像被分割为可能属于同一物体的区域。在做图像分割时, 了解共体的应用领域是有帮助的, 这样就可以比较容易地处理|噪声和与错误阁像数据有关的其他问题。
- 第三层:几何表示,保存2D和3D形状知识。形状的hl化是i非常困难的,但也是十分重要的。在做普通而复杂的有关实际物体受光照和运动影响的模拟时, 儿何表示是有用的。在将由摄像机得到的自然光栅罔像与计算机图形学(计算机辅助设计、桌面印刷)使用的数据之间作转换时,也要用到几何表示。
- 第四层:关系模型。关系模型使我们能更有效地, 并且在更高的抽象层次上处理数据。一般需要使用一些有关待解决问题的先验知识,通常会涉及人工智能技术,从图像中获得的信息可以表示成语义网络或框架。
传统图像数据结构
传统的图像数据结构有矩阵、链、图、物体属性表、关系数据库,它们不仅对于直接表示图像信息是重要的,而且还是更复杂的图像分层表示方法的基础。
矩阵
矩阵是低层图像表示的最普通的数据纣构,矩阵元素是整型的数值,对应于采样栅格中的相应像素的亮度或其他属性。这类图像数据通常是图像获取设备的直接输出。矩形和六边形来样栅格的像京都可以用矩阵来表示,数据与矩阵元素的对应关系对于知形栅格来说是显然的,对于六边形栅格来说图像中的每个偶数行都要向右移平个像素。
矩阵中的图像信息可以通过像素的坐标得到,坐标对应于行和列的标号。矩阵是图像的-个完整表示, 与阁像数据的内容无关,它隐含着图像组成部分之间的空间关系(spatial relations),这些图像组成部分在语义t具有重要性。在图像的情况下,空间是二维的。一个非常自然的空间关系是相邻关系(neighborhood relation)。
用矩阵表示的特殊图像有:
- 二值图像
- 多光谱图像
- 多层图像数据结构
多数编程语言用标准的数组数据结构友示矩阵,历史上存储限制曾经是图像应用的一个显著障碍,但现在不存在这样的担忧了。
矩阵中有大量的图像数据。如果首先从原始的图像矩阵得出全局信息,由于全局信息更紧凑并且占用的存储少,那么算法就可以加速。从概率的角度观察图像,标准化的直方图是如下现象的概率密度的估计:一个图像的像素具有某个亮度。
共生矩阵
另一个全局信息的例子是共生矩阵 。

考虑共生矩阵的主要原因是其描述纹理的能力。
积分图像
积分图像 是一种能够描述全局信息的矩阵表示方法。
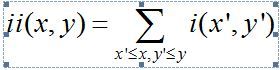
其中f是原图像。积分图像能够高效地用递归方法在单次图像遍历中计算出来:

积分图像这个数据结构主要用来快速计算多个尺度的简单矩形图像特征。这种特征能用在快速的目标识别和目标跟踪。
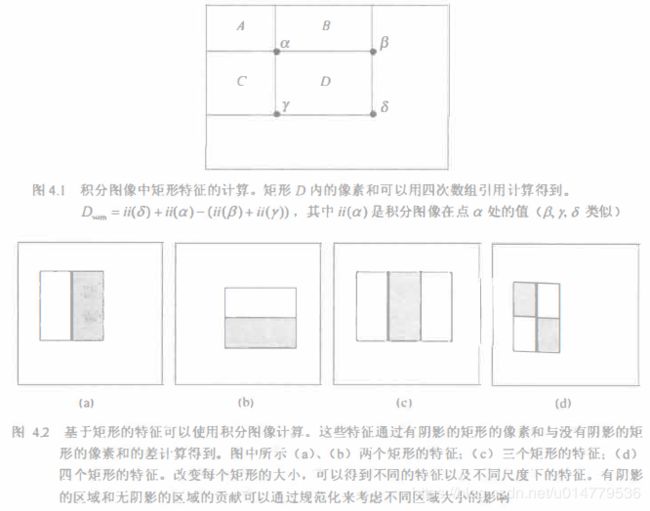
链
链在计算机视觉中用于描述物体的边界。链的元素是一个基本符号,这种方法使得在计算机视觉任务中可以使用形式语言理论。
链码 常用于描述物体的边界,或者图像中一个像素宽的线条。边界由其参考像素的坐标和一个符号序列来定义,符号对应于几个事先定义好了方向的单位长度的线段。

如果需要从链码中得到局部信息,就必须系统地搜索整个链码。
用链码描述罔像适合基于形式语言理论的句法模式识别。
行程编码(run length coding) 已经很长时间内被用于图像矩阵中符号串的表示。
拓扑数据结构
拓扑数据结构将图像描述成一组元索及其相互关系,这些关系通常用图结构来表示。
区域邻接图(region adjacency graph) 是这类数据结构的一个典型,其中结点对应于区域,相邻的区域川弧连接起来。

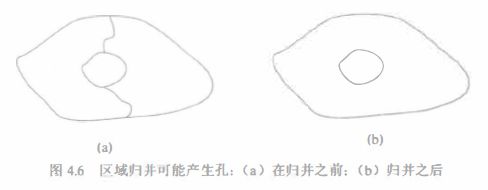
关系结构
使用关系纣构的描述适合f向层次的图像理解工作。在这种情况下, 类似于数据库检索,用关键词搜索适用于加速整个处理过程。

分层数据结构
计算机视觉在本质七是计算代价十分高昂的,仅考虑所需处理的巨大数据量就会得出这个结论。
不幸的是,很多计算机视觉问题都很难在多处理机间分配计算负担,或者根本就无法分解。分层数据结构使得使用一些特殊算法成为可能,这些算法在相对小的数据量基础t决定处理策略。
它们使用知识而不是强力来减轻计算负担并提高处照速度,只对阁像的实质部分才在最精细的分辨率t工作。我们要介绍两种典型的结构,金字塔(pyramids)和四叉树(quad trees)。
金字塔
金字塔属于最简单的分层数据结构。我们区分两种这样的结构,即M型金字塔和T型金字塔。
四叉树
四叉树是对T型金字塔的改进。
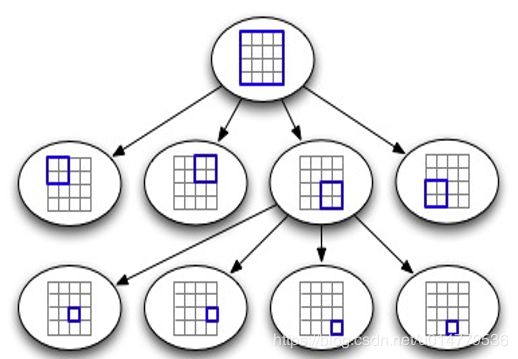
用同叉树来表示图像的优点是,对丁阁像相加、物体面积计算和统计矩(moments)计算存在简单的算法。四叉树和金字塔分层表示的主要缺点是 ,它们依赖于物体的位置、方向和相对大小。
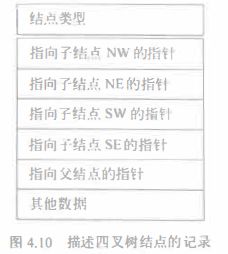
用叶码(leaf code)来友示四叉树可以降低存储需求。
问义树已经行广泛的用途, 特别是在地理信息系统(Geographic Informati on System, GIS)领域 ,
