使用边界坐标来查找距某个纬经度一定范围内的点
原文地址:http://janmatuschek.de/LatitudeLongitudeBoundingCoordinates#RefBronstein
使用边界坐标来查找距某个纬经度一定范围内的点
摘要
本文介绍如何有效地在数据库中查询与球面坐标(纬度和经度)中给出的点之间一定距离内的位置。该方法计算可用于数据库索引扫描的边界坐标 - 就像我们使用最小边界矩形来加速笛卡尔空间中的查询一样。它对于短距离和长距离都是准确的,并且适用于任何地理位置,即使它靠近极点或本初个子午线。
目录
- 计算两点之间的距离
- 在不使用索引的情况下查找距离内的位置
- 使用索引查找距离内的位置
- 计算最小和最大纬度
- 计算最小和最大经度 - 不正确的方法
- 计算最小和最大经度 - 正确的方法
- 处理极点和本初子午线
- SQL查询
- Java 源码
GeoLocation类GeoLocation类使用
- 其他语言的实现
1、计算两点之间的距离
在半径为R的球体 的表面上的给定两个点 P1=(lat1, lon1) 和 P2=(lat2, lon2),计算两点之间的最短距离(球体表面)。可以使用下面的公式计算:
distance= arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon1 - lon2)) * R (1)
例如,自由女神像在(40.6892°,-74.0444°)=(0.7102 rad,-1.2923 rad)与艾菲尔铁塔之间的距离(48.8583°,2.2945°)=(0.8527 rad,0.0400 rad) - 假设地球的球半径R = 6371 km :
distance = arccos(sin(0.7102) * sin(0.8527)+ cos(0.7102) * cos(0.8527) * cos(-1.2923 - 0.0400))* 6371 km
= 5837 km (2)
2、在不使用索引的情况下查找某个距离内的位置
假设我们想要在数据库中找到距离M =(lat,lon)=(1.3963 rad,-0.6981 rad)的距离d = 1000 km 内的位置。假设我们有一个名为Places的表,其中Lat和Lon列以弧度表示坐标(SQL的三角函数表示弧度),那么我们可以使用这个SQL查询:
SELECT * FROM Places WHERE acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) * 6371 <= 1000;
此查询的问题在于,由于WHERE子句中公式的复杂性,我们的数据库系统将无法使用Lat和Lon列上的索引。
3、使用索引查找距离内的位置
为了利用Lat和Lon列上的索引,我们可以使用类似于笛卡尔空间中的边界矩形方法的方法。
我们把到点 M 的距离为 d 的所有点构成的圆称为查询圆。
边界坐标 (latmin, lonmin) 和 (latmax, lonmax) 它们是完全包含查询圆的边界矩形(在球体上)的对角,所以这个矩形外的点肯定不在查询圆内,因此,为了找到查询圆内的点,我们只需要考虑边界矩形内的点。
可以使用索引快速找到这些点(称为候选位置)(有关SQL查询,请参阅第3.5节)。以下小节介绍了如何计算 边界坐标。
定义为查询圆的角半径:
r = d / R =(1000 km)/(6371 km)= 0.1570。
3.1 计算最小和最大纬度
在从A点到B点的半径R = 6371km 的圆上移动,使得在A和B之间存在角弧长 r = 0.1570 意味着覆盖 d = 1000km的距离。子午线位于半径为r的大圆上,因此我们可以沿着子午线移动,即保持经度不变,将r 对 lat进行简单的减法/相加,得到查询圆内所有点的最小/最大纬度。
假设圆心 M=(lat, lon)=(1.3963 rad, -0.6981 rad):
latmin = lat - r = 1.2393 rad (3)
latmax = lat + r = 1.5532 rad (4)
注意,如果一个极点位于查询圈内,则必须特别注意。详见3.4节。
3.2 计算最小和最大经度 - 不正确的方法
计算最小经度和最大经度的一种方法是保持纬度不变并改变经度,即沿着纬度的圆移动。本节将说明这种方法给出的结果是不准确的。
沿着纬度的圆移动则意味着沿着一个小圆(相对于赤道的圆)移动。假设纬度为 lat=1.3963 rad ,在纬度处的圆的半径
Rs = R·cos(lat) = 1106 km ,则现在 d=1000 km 对应的角半径 rs = d/Rs = d/(R·cos(lat)) = 0.9039。
所以,在一个纬度圆上覆盖d = 1000km,就可以得到经度lons = lon ± d/(R·cos(lat)) = -0.6981 rad ± 0.9039 rad。
但这不是向任何方向移动d=1000公里所能得到的最小/最大经度!
这是因为我们在一个小圆上移动了距离,但是小圆的距离大于大圆的距离。
虽然 M=(lat, lon)=(1.3963 rad, -0.6981 rad) 和 Ps=(lat, lons)=(1.3963 rad, -1.6020 rad) 在小圆上的距离d=1000公里,
但在大圆上我们可以从 M 点到 Ps点 会得到更短的路径 。根据公式(1),这条路径的长度为967公里。
所以我们可以再移动33公里,仍然在查询范围内。尤其是,我们可以分别获取到更小、更大的经度。
因此,使用 lon ± d/(R·cos(lat)) 作为经度的边界值,会遗漏一些实际在d范围内的位置。例如,P3=(1.4618 rad, -1.6021 rad)点在计算边界“框”之外,虽然它到M的距离只有872 km。这是一个超过12%的误差!
3.3 计算最小和最大经度 - 正确的方法
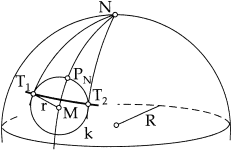
沿着一个纬度圈移动(经线)以找到最小和最大经度根本不管用,如图1所示:查询圆上具有最小/最大经度T1和T2的点不在与中心 M 点处在相同的纬度圈而是更接近极点。这些点的坐标公式可以在好的数学手册中找到。它们是:
latT = arcsin(sin(lat)/cos( r )) = 1.4942 rad
lonmin = lonT1 = lon - Δlon = -1.8184 rad
lonmax = lonT2 = lon + Δlon = 0.4221 rad
其中
Δlon = arccos( ( cos( r) - sin(latT) · sin(lat) ) / ( cos(latT) · cos(lat) ) )
= arcsin(sin( r )/cos(lat)) = 1.1202 rad (8)
请注意,如果本初子午线位于查询圆圈内,则必须特别小心。详情请参阅第3.4节。
3.4 处理极点和本初子午线
如果3.1节中定义的lat max大于 π/ 2,则北极位于查询圆内,这意味着所有子午线的部分也在查询圆内。因此,在这种情况下,边界坐标是(latmin,-π)和(π/ 2,π)。如果latmin小于 -π/ 2,那么南极在查询圆内,并且边界坐标是(-π/ 2,-π)和(latmax,π)。
如果在3.3节在限定的lonmin/max,是在有效的经度值[-π,π]的范围之外,则180度经线是查询圆内。在那种情况下,可以使用(latmin,-π)和(latmax,π)作为边界坐标,即具有类似于球体周围的带状的东西。但那将包括许多实际上并不在距离内的候选地点。或者,可以使用两个边界“框”,并且候选地点在其中一个中就足够了。如果lonmin<-π,则两组边界坐标为(lat min,lonmin +2π),(lat max,π)和(latmin,-π),(lat max,lonmax)。如果lonmax>π,则两组边界坐标为(lat min,lonmin),(lat max,π)和(lat min,-π),(lat max,lon max- 2π)。
3.5 SQL查询
我们已经计算了边界坐标(lat min,lonmin)=(1.2393 rad,-1.8184 rad)和(lat max,lonmax)=(1.5532 rad,0.4221 rad),我们可以在SQL查询中使用它们。在下文中,假设纬度和经度(均以弧度表示)存储在两个单独的列中,其中每个列都支持范围查询(例如,B树)。如果您的数据库管理系统在这些列上支持点数据类型和空间索引(例如R树),您也可以使用它。
使用边界坐标将过滤器与SQL语句中的大圆距离公式组合的方法有很多种:
- 简单地将条件与AND组合:
大多数查询优化器足够聪明,可以执行索引扫描以快速找到满足的位置,(Lat >= 1.2393 AND Lat <= 1.5532) AND (Lon >= -1.8184 AND Lon <= 0.4221)并仅为每个剩余的候选结果评估大圆距离的公式。SELECT * FROM Places WHERE (Lat >= 1.2393 AND Lat <= 1.5532)AND(Lon> = -1.8184 AND Lon <= 0.4221) AND acos(sin(1.3963)* sin(Lat)+ cos(1.3963)* cos(Lat )* cos(Lon - (-0.6981)))<= 0.1570; - WHERE子句中的预过滤器和HAVING子句中更具体的公式:
SELECT * FROM Places WHERE (Lat >= 1.2393 AND Lat <= 1.5532) AND (Lon >= -1.8184 AND Lon <= 0.4221) HAVING acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= 0.1570; - 子查询中的预过滤:
SELECT * FROM ( SELECT * FROM Places WHERE (Lat >= 1.2393 AND Lat <= 1.5532) AND (Lon >= -1.8184 AND Lon <= 0.4221) ) WHERE acos(sin(1.3963) * sin(Lat) + cos(1.3963) * cos(Lat) * cos(Lon - (-0.6981))) <= 0.1570;
4 Java 源码
4.1 GeoLocation 类
/**
* Represents a point on the surface of a sphere. (The Earth is almost
* spherical.)
*
* To create an instance, call one of the static methods fromDegrees() or
* fromRadians().
*
* This code was originally published at
*
* http://JanMatuschek.de/LatitudeLongitudeBoundingCoordinates#Java.
*
* @author Jan Philip Matuschek
* @version 22 September 2010
*/
public class GeoLocation {
private double radLat; // latitude in radians
private double radLon; // longitude in radians
private double degLat; // latitude in degrees
private double degLon; // longitude in degrees
private static final double MIN_LAT = Math.toRadians(-90d); // -PI/2
private static final double MAX_LAT = Math.toRadians(90d); // PI/2
private static final double MIN_LON = Math.toRadians(-180d); // -PI
private static final double MAX_LON = Math.toRadians(180d); // PI
private GeoLocation () {
}
/**
* @param latitude the latitude, in degrees.
* @param longitude the longitude, in degrees.
*/
public static GeoLocation fromDegrees(double latitude, double longitude) {
GeoLocation result = new GeoLocation();
result.radLat = Math.toRadians(latitude);
result.radLon = Math.toRadians(longitude);
result.degLat = latitude;
result.degLon = longitude;
result.checkBounds();
return result;
}
/**
* @param latitude the latitude, in radians.
* @param longitude the longitude, in radians.
*/
public static GeoLocation fromRadians(double latitude, double longitude) {
GeoLocation result = new GeoLocation();
result.radLat = latitude;
result.radLon = longitude;
result.degLat = Math.toDegrees(latitude);
result.degLon = Math.toDegrees(longitude);
result.checkBounds();
return result;
}
private void checkBounds() {
if (radLat < MIN_LAT || radLat > MAX_LAT ||
radLon < MIN_LON || radLon > MAX_LON)
throw new IllegalArgumentException();
}
/**
* @return the latitude, in degrees.
*/
public double getLatitudeInDegrees() {
return degLat;
}
/**
* @return the longitude, in degrees.
*/
public double getLongitudeInDegrees() {
return degLon;
}
/**
* @return the latitude, in radians.
*/
public double getLatitudeInRadians() {
return radLat;
}
/**
* @return the longitude, in radians.
*/
public double getLongitudeInRadians() {
return radLon;
}
@Override
public String toString() {
return "(" + degLat + "\u00B0, " + degLon + "\u00B0) = (" +
radLat + " rad, " + radLon + " rad)";
}
/**
* Computes the great circle distance between this GeoLocation instance
* and the location argument.
* @param radius the radius of the sphere, e.g. the average radius for a
* spherical approximation of the figure of the Earth is approximately
* 6371.01 kilometers.
* @return the distance, measured in the same unit as the radius
* argument.
*/
public double distanceTo(GeoLocation location, double radius) {
return Math.acos(Math.sin(radLat) * Math.sin(location.radLat) +
Math.cos(radLat) * Math.cos(location.radLat) *
Math.cos(radLon - location.radLon)) * radius;
}
/**
* Computes the bounding coordinates of all points on the surface
* of a sphere that have a great circle distance to the point represented
* by this GeoLocation instance that is less or equal to the distance
* argument.
* For more information about the formulae used in this method visit
*
* http://JanMatuschek.de/LatitudeLongitudeBoundingCoordinates.
* @param distance the distance from the point represented by this
* GeoLocation instance. Must me measured in the same unit as the radius
* argument.
* @param radius the radius of the sphere, e.g. the average radius for a
* spherical approximation of the figure of the Earth is approximately
* 6371.01 kilometers.
* @return an array of two GeoLocation objects such that:
* - The latitude of any point within the specified distance is greater
* or equal to the latitude of the first array element and smaller or
* equal to the latitude of the second array element.
* - If the longitude of the first array element is smaller or equal to
* the longitude of the second element, then
* the longitude of any point within the specified distance is greater
* or equal to the longitude of the first array element and smaller or
* equal to the longitude of the second array element.
* - If the longitude of the first array element is greater than the
* longitude of the second element (this is the case if the 180th
* meridian is within the distance), then
* the longitude of any point within the specified distance is greater
* or equal to the longitude of the first array element
* or smaller or equal to the longitude of the second
* array element.
*
*/
public GeoLocation[] boundingCoordinates(double distance, double radius) {
if (radius < 0d || distance < 0d)
throw new IllegalArgumentException();
// angular distance in radians on a great circle
double radDist = distance / radius;
double minLat = radLat - radDist;
double maxLat = radLat + radDist;
double minLon, maxLon;
if (minLat > MIN_LAT && maxLat < MAX_LAT) {
double deltaLon = Math.asin(Math.sin(radDist) /
Math.cos(radLat));
minLon = radLon - deltaLon;
if (minLon < MIN_LON) minLon += 2d * Math.PI;
maxLon = radLon + deltaLon;
if (maxLon > MAX_LON) maxLon -= 2d * Math.PI;
} else {
// a pole is within the distance
minLat = Math.max(minLat, MIN_LAT);
maxLat = Math.min(maxLat, MAX_LAT);
minLon = MIN_LON;
maxLon = MAX_LON;
}
return new GeoLocation[]{fromRadians(minLat, minLon),
fromRadians(maxLat, maxLon)};
}
}
Download GeoLocation.java
4.2 GeoLocation 类使用
/**
* See
*
* http://JanMatuschek.de/LatitudeLongitudeBoundingCoordinates#Java
* for the GeoLocation class referenced from this code.
*
* @author Jan Philip Matuschek
* @version 26 May 2010
*/
public class GeoLocationDemo {
/**
* @param radius radius of the sphere.
* @param location center of the query circle.
* @param distance radius of the query circle.
* @param connection an SQL connection.
* @return places within the specified distance from location.
*/
public static java.sql.ResultSet findPlacesWithinDistance(
double radius, GeoLocation location, double distance,
java.sql.Connection connection) throws java.sql.SQLException {
GeoLocation[] boundingCoordinates =
location.boundingCoordinates(distance, radius);
boolean meridian180WithinDistance =
boundingCoordinates[0].getLongitudeInRadians() >
boundingCoordinates[1].getLongitudeInRadians();
java.sql.PreparedStatement statement = connection.prepareStatement(
"SELECT * FROM Places WHERE (Lat >= ? AND Lat <= ?) AND (Lon >= ? " +
(meridian180WithinDistance ? "OR" : "AND") + " Lon <= ?) AND " +
"acos(sin(?) * sin(Lat) + cos(?) * cos(Lat) * cos(Lon - ?)) <= ?");
statement.setDouble(1, boundingCoordinates[0].getLatitudeInRadians());
statement.setDouble(2, boundingCoordinates[1].getLatitudeInRadians());
statement.setDouble(3, boundingCoordinates[0].getLongitudeInRadians());
statement.setDouble(4, boundingCoordinates[1].getLongitudeInRadians());
statement.setDouble(5, location.getLatitudeInRadians());
statement.setDouble(6, location.getLatitudeInRadians());
statement.setDouble(7, location.getLongitudeInRadians());
statement.setDouble(8, distance / radius);
return statement.executeQuery();
}
public static void main(String[] args) {
double earthRadius = 6371.01;
GeoLocation myLocation = GeoLocation.fromRadians(1.3963, -0.6981);
double distance = 1000;
java.sql.Connection connection = ...;
java.sql.ResultSet resultSet = findPlacesWithinDistance(
earthRadius, myLocation, distance, connection);
...;
}
}
Download GeoLocationDemo.java