目录
- 采样方法
- Inverse CDF
- 接受-拒绝采样(Acceptance-Rejection Sampling)
- 蒙特卡洛方法
采样方法
实际应用中,经常需要获得服从某一分布的样本集。不过,手动生成一般来说不太现实,需要求助于计算机,而计算机则只能实现对均匀分布进行抽样。其他的分布,甚至如高斯分布都是无法实现的。不过,通过均匀分布,可间接地生成服从其他分布的样本。这点很重要,下面会看到,所有的随机模拟都从均匀分布开始的,然后经过所需分布的约束,获得所需样本的。
Inverse CDF
最简单,最直观的方法是Inverse CDF,也称为Inverse transform sampling。 借助于PDF(概率密度函数)与CDF(累积分布函数)的关系进行抽样。
举个简单例子,设某一概率密度函数为:
\[ f(x) = \frac{e^x}{1+e^{x}}\cdot\frac{1}{1+e^x}\qquad x\in [-\infty,+\infty] \]
这个密度函数的累积分布函数可以很容易的求得:
\[ F(x) =P\{X\le x\}= \frac{1}{1+e^{-x}}\qquad x\in [-\infty,+\infty] \]
假设有一个样本集来自此分布函数,那么,将每个样本带入累积分布函数,都可以得到对应的\(F(x)\)的值。如果样本集来自随机采样,与其对应的累积分布函数值也会是随机的,且服从(0,1)上的均匀分布。于是,为了得到这个的样本,可以将这个过程颠倒过来,即在(0,1)的均匀分布上随机采样,然后带入累积分布函数的反函数中,即可得到服从此分布的样本 。
比如,\(F(x) = 0.8\),我们需要求出其中的x是多少,这个x即是服从上述分布的样本。求取的思路也很直观,先求出\(F(x)\)的反函数,然后将0.8带入,即可求出x的值是多少。上述累积分布反函数:
\[ F'(u) = -\log((1-u)/u) \qquad u\in (0,1) \]
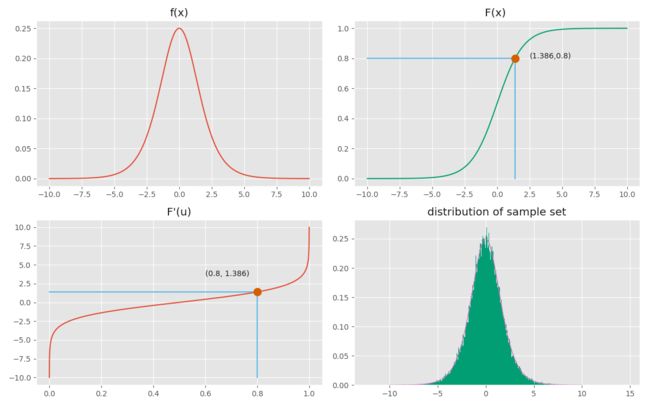
当 u =0.8时,带入可得 \(x = F'(u) \approx 1.386\). 这个x即是服从上述分布的样本,重复这个过程即可得到所需样本集(如图1 d图)。
图1 (a)概率密度函数;(b) 累积分布函数;(c) 累积分布函数的反函数;(d) 样本集的分布。
可见,此种方法适用于可显式地求得累积分布函数的反函数的分布。一般地,Inverse transform sampling 方法的抽样过程可归纳为:
Given Cumulative Distribution Function of interest cdf(u), get its inverse function: icdf(x)
samples = list()
while True:
sample x from uniform(0,1)
y = icdf(x)
samples.append(y)
if satisfy some sampling condition:
break
对于常见的分布,如高斯分布不易求得其累积分布函数的常见分布,前人也给出了解决方法,如Box-Muller变换。
但对于不常见的分布,Inverse transform sampling应用起来就不太方便,因为累积分布函数的反函数不易求,甚至无法显式地求出。这时就需要用其他方法,比如下面提到的接受-拒绝采样(Acceptance-Rejection Sampling), 重要性采样等等.
接受-拒绝采样(Acceptance-Rejection Sampling)
当对某一分布\(p(x)\)直接抽样比较困难时, 可以通过对另一相对容易的分布\(q(x)\)进行抽样,然后保留其中服从\(p(x)\)的样本,而剔除不服从\(p(x)\)的无效样本。\(q(x)\)称为建议分布函数(proposal distribution)。
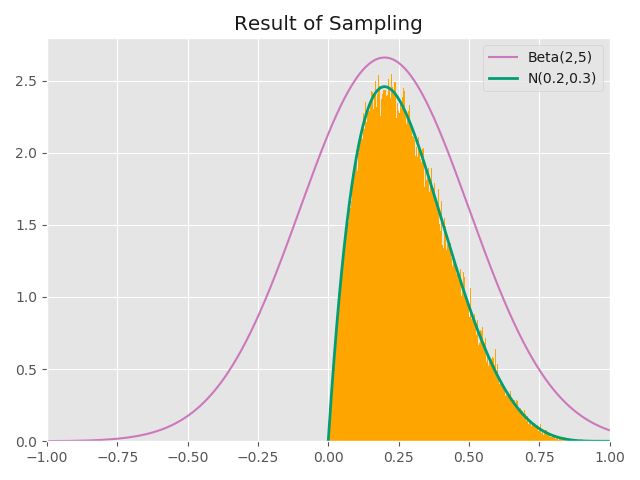
例如,要对beta(2, 5)进行抽样,beta分布的反函数不易求得,上述的反函数方法不太适用。那么可以引入一个相对容易抽样的分布,如正态分布,甚至均匀分布等,这里不妨使用正态分布,比如N(0.2,1)。如上所述,抽样可转化为平面上的积分,需要proposal distribution 包裹或者说‘罩住’待抽样分布,为此需将proposal distribution乘以一个系数 k,这里取k=2,具体如下图:
接下来就可以进行采样了:
从q(x) (proposal distribution,这里为N(0.2,0.3)随机地抽取一个样本, \(x_i\);
从均匀分布U(0,1)中随机抽取一个样本 \(u_i\);
比较\(u_i\)与 \(\alpha = \frac{p(x)}{k\cdot q(x)}\):
如果 \(u_i\le \alpha\) 则认为 \(x_i\)为服从p(x)的有效样本,反之,则认为无效,舍弃。
重复上述步骤直至抽样结束。其中\(\alpha\)称为接受率,这是此方法名字的由来。
下图为实验结果:
接受拒绝采样的证明,即是证明,经过上述过程得到的样本是否服从目标分布p(x):
设目标分布与建议分布分别用T,Q表示,其对应的概率密度函数分别为t(x)与q(x), 证明此采样方法的有效性即是证明:
\[ P\left(Y\le y|U\le \frac{t(Y)}{k\cdot q(Y)}\right) = T(y) \]
其中,\(U\)为服从(0,1)均匀分布的随机变量。
\[ prof:\\ \begin{array}\\ P\left(Y\le y|U\le \frac{t(Y)}{k\cdot q(Y)}\right) &=& \frac{P\left(Y\le y , U\le \frac{t(Y)}{k\cdot q(Y)}\right)}{P\left(U\le \frac{t(Y)}{kq(Y)}\right)}\\ &=& \frac{P\left(Y\le y , U\le \frac{t(Y)}{k\cdot q(Y)}\right)}{\int_{-\infty}^{\infty} P\left(U\le \frac{t(Y)}{kq(Y)}|Y=y\right)q(y)dy}\\ &=& \frac{P\left(Y\le y , U\le \frac{t(Y)}{k\cdot q(Y)}\right)}{\int_{-\infty}^{\infty} \frac{t(y)}{kq(y)}q(y)dy}\\ & =& \frac{P\left(Y\le y , U\le \frac{t(Y)}{k\cdot q(Y)}\right)}{\frac{1}{k}}\\ &=& k\cdot P\left(Y\le y , U\le \frac{t(Y)}{k\cdot q(Y)}\right)\\ &=& k\cdot \int_{-\infty}^{y}\int_{0}^{ \frac{t(Y)}{k\cdot q(Y)}}q(Y)\cdot 1\cdot dUdY\\ & = & \int_{-\infty}^y t(Y)dY\\ &=& T(y). \end{array} \]
蒙特卡洛方法
蒙特卡洛方是一个赌场的名字,其作为随机模拟方法的名称有说是因为玩笑也有人说是因为机密。
蒙特卡洛方法最初目的是解决直接求解积分(或求和)有困难的问题,因为积分不能直接求得,需要通过某种方法来近似,蒙特卡洛方法即采用随机抽样的方法,在大数定律的作用下,随着抽样次数增加,近似会越来越精确。
设在[a,b]上,函数\(0 \le f(x)\le M\), 计算:
\[ I=\int_{a}^{b} f(x) \mathrm{d} x \]
图中阴影部分被矩形所包,欲求此部分面积,可在这个矩形内随机的投点,某点落在阴影部分的概率为:
\[ P=\frac{\int_{a}^{b} f(x) \mathrm{d} x}{(b-a) M}=\frac{I}{(b-a) M} \]
根据大数定律,当投点次数很大时,可将 \(\frac{n}{N}\)作为P的近似值,其中n为落入阴影中的点数,而N为投点总数。于是:
\[ I=P\cdot M(b-a)=\frac{n M(b-a)}{N} \]
如果知道\(f(x)\),可以在[a,b]上随机的抽样\(\{x_0,x_2,...,x_{n-1}\}\). 然后计算分别计算\(,求得阴影面积f(x_i),求得阴影面积\) :
\[ I = \frac{b-a}{n} \sum_{i=0}^{n-1} f\left(x_{i}\right) \]
重要性采样:
重要性采样方法作为一种蒙特卡洛方法,可降低估计方差。
重要性采样考虑的是通过蒙特卡洛方法求取\(\mu = E[f(X)]\), 其中X是服从分布\(p(x)\):
\[ \mu = E f(X) = \int_X p(x)\cdot f(x)dx \]
当\(p(x)\)不容易抽样时,重要性采样如接受-拒绝采样一样引入了另一个相对容易采样的分布,不过重要性采样没有对样本进行接受与否的判定,而是对所有样本进行加权平均,其想法也是非常的直观:
\[ \mu = Ef(x) = \int_X p(x)\cdot f(x)dx = \int_X \frac{p(x)}{q(x)}\cdot q(x)\cdot f(x)dx = \int_X w(x)\cdot q(x)dx \]
其中, \(w(x) = \frac{p(x)}{q(x)}\).称为重要性采样比率(Importance Sampling Ratio 或 likelihood ratio).
MCMC(Markov Chain Monte Carlo)
在随机过程中,马尔可夫性质表示当给定t时刻的状态,那么t+1时刻随机过程的状态概率就是确定的:
\[ P\left(X_{t+1}=x | X_{t}, X_{t-1}, \cdots\right)=P\left(X_{t+1}=x | X_{t}\right) \]
即状态转移的概率只依赖于前一个状态,而与更早的状态无关。
举个例子,某生物实验室,为科研需要培养大量的斑马鱼,未经实验的斑马鱼假设只有红黄蓝三种颜色,实验室的科研人员发现在稳定的实验室环境内,三种颜色的鱼都会生出其色颜色的斑马鱼(为简单,这里假定只有相同颜色的斑马鱼才会交配。),比如红色的斑马鱼其后代有0.72概率还是红色,而有0.17的概率生成黄色斑马鱼,有0.11的概率生成蓝色斑马鱼。具体的:
\[ P=\left[ \begin{array}{ccc}{0.72} & {0.17} & {0.11} \\ {0.33} & {0.14} & {0.53} \\ {0.12} & {0.77} & {0.11}\end{array}\right] \]
发现这了这个转移概率矩阵后,科研人员对每一代的斑马鱼的比例都了若指掌。比如有一次他们进购了三种鱼的比率是【0.2,0.3,0.5】.
| Generation | Red | Blue | Yellow |
|---|---|---|---|
| 0 | 0.2 | 0.3 | 0.5 |
| 1 | 0.303 | 0.461 | 0.236 |
| 2 | 0.399 | 0.298 | 0.304 |
| 3 | 0.422 | 0.343 | 0.235 |
| 4 | 0.445 | 0.301 | 0.254 |
| 5 | 0.45 | 0.313 | 0.236 |
| 6 | 0.456 | 0.302 | 0.242 |
| 7 | 0.457 | 0.306 | 0.237 |
| 8 | 0.458 | 0.303 | 0.238 |
| 9 | 0.459 | 0.304 | 0.237 |
| 10 | 0.459 | 0.303 | 0.238 |
| 11 | 0.459 | 0.304 | 0.237 |
| 12 | 0.459 | 0.303 | 0.237 |
| 13 | 0.459 | 0.303 | 0.237 |
| 14 | 0.459 | 0.303 | 0.237 |
| ... | ... | ... | ... |
当到第11代时,三种颜色的比例就稳定了。科研人员觉得很有意思,于是他们又一次购买鱼苗时,将比例变成了[0.05,0.94,0.01] 这样一个比较奇怪的比例:
| Generation | Red | Blue | Yellow |
|---|---|---|---|
| 0 | 0.05 | 0.94 | 0.01 |
| 1 | 0.347 | 0.148 | 0.505 |
| 2 | 0.359 | 0.468 | 0.172 |
| 3 | 0.434 | 0.259 | 0.307 |
| 4 | 0.435 | 0.346 | 0.219 |
| 5 | 0.454 | 0.291 | 0.255 |
| 6 | 0.453 | 0.315 | 0.232 |
| 7 | 0.458 | 0.3 | 0.242 |
| 8 | 0.458 | 0.306 | 0.236 |
| 9 | 0.459 | 0.302 | 0.239 |
| 10 | 0.459 | 0.304 | 0.237 |
| 11 | 0.459 | 0.303 | 0.238 |
| 12 | 0.459 | 0.304 | 0.237 |
| 13 | 0.459 | 0.303 | 0.237 |
| 14 | 0.459 | 0.303 | 0.237 |
| ... | ... | ... | ... |
同样地,经过几代之后,比例再次稳定且与上次相同。这不是巧合,这是绝大多数马氏链都具有的收敛性质:
对于一个非周期的马尔可夫链,其状态转移概率矩阵为P,且其各个状态都是连通的,那么\(\lim _{n \rightarrow \infty} P_{i j}^{n}\)存在且与 i无关,如果记\(\lim _{n \rightarrow \infty} P_{i j}^{n}=\pi(j)\),那么我们可得到:
1)
\[ \lim _{n \rightarrow \infty} P^{n}=\left[ \begin{array}{ccccc}{\pi(1)} & {\pi(2)} & {\cdots} & {\pi(j)} & {\cdots} \\ {\pi(1)} & {\pi(2)} & {\cdots} & {\pi(j)} & {\cdots} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {\pi(1)} & {\pi(2)} & {\cdots} & {\pi(j)} & {\cdots} \\ {\cdots} & {\ldots} & {\cdots} & {\cdots} & {\cdots}\end{array}\right] \]
2)
\[ \pi(j)=\sum_{i=0}^{\infty} \pi(i) P_{i j} \]
3) \(\pi\)是 方程\(\pi P=\pi\)唯一非负解,其中\(\pi=[\pi(1), \pi(2), \cdots, \pi(j), \cdots], \quad \sum_{i=0}^{\infty} \pi_{i}=1\),称为马氏链的平稳分布。(PS: \(\pi\) 是概率分布,不是某一确定数值。)
这个是马尔可夫链很重要的收敛性质,后面的所有的都是基于此性质的。在这个性质中,'非周期'表示的是随机过程的状态转化不是循环的,即对任意状态i,d为集合\(\left\{n | n \geq 1, P_{i i}^{n}>0\right\}\)的最大公约数,其值为1则表明马氏链是非周期的。 '各个状态连通'表明状态转移概率矩阵中各个元素都是非0的。对2)中有证明也非常的直观:
\[ \begin{aligned} P\left(X_{n+1}=j\right) &= \sum_{i=0}^{\infty} P\left(X_{n}=i\right) P\left(X_{n+1}=j | X_{n}=i\right) \\ &=\sum_{i=0}^{\infty} P\left(X_{n}=i\right) P_{i j} \end{aligned} \]
同时对两边取极限,即可得到\(\pi(j)=\sum_{i=0}^{\infty} \pi(i) P_{i j}\). 另外,马尔可夫链的状态数可是有限的,也可以是无限的,即上述性质适用于离散概率分布与连续概率分布。这里所谓“平稳分布”即是指经概率转移矩阵的作用,分布不再变化。
当已知某平稳分布对应的转移概率矩阵P,就可得到此平稳分布的样本集。由上述性质可知,无论初始概率分布(\(\pi_0(x)\))为何,经过多轮(比如n轮)概率转移后,就会收敛到平稳概率分布,即:
\[ \pi_{n}(x)=\pi_{n+1}(x)=\pi_{n+2}(x)=\ldots=\pi(x) \]
因此,可从简单分布中抽样,得到初始样三本\(x_0\),然后根据条件概率分布\(P(x_1|x_0)\)得到\(x_1\), 依次类推,根据\(P(x_2|x_1),P(x_3|x_2),...,P(x_n|x_{n-1}),...,P(x_{n+m}|p_{n+m-1})\) 分别得到\(x_2,x_3,...,x_n,...,x_{n+m}\),其中\((x_{n+1},x_{n+2},...,x_{n_m})\) 即是服从所需平稳分布的样本集。
上面的收敛性质给予我们很大的启发,对于某分布\(\pi(x)\),要得到其对应的样本,只需构造一个具有转移概率矩阵为P的马尔可夫链,使其收敛的平稳分布为\(p(x)\)。那么如何做呢?这就涉及一个很重要的概念,称为细致平衡条件:如果非周期马尔可夫链的状态转移矩阵P的概率分布\(\pi(x)\)对于所有的i,j满足:
\[ \pi(i) P(i, j)=\pi(j) P(j, i) \]
则称为概率分布\(\pi(x)\)是状态转移矩阵P的平稳分布。
这个条件的很直观:
\[ \begin{array}{l}{\sum_{i=1}^{\infty} \pi(i) P_{i j}=\sum_{i=1}^{\infty} \pi(j) P_{j i}=\pi(j) \sum_{i=1}^{\infty} P_{j i}=\pi(j)} \\ {\Rightarrow \pi P=\pi}\end{array} \]
不过,通常情况下,这个条件无法满足,即很难找到这样一个马尔可夫链对应的转移概率矩阵,使得上式成立。比如转移概率为Q的马尔可夫链,可以验证,一般地:
\[ \pi(i) Q(i, j) \neq \pi(j) Q(j, i) \]
为使等式成立,可以引入另一个矩阵\(\alpha\),即:
\[ \pi(i) Q(i, j) \alpha(i, j)=\pi(j) Q(j, i) \alpha(j, i) \]
为达此目的,\(\alpha\)需要满足些条件:
\[ \begin{aligned} \alpha(i, j) &=\pi(j) Q(j, i) \\ \alpha(j, i) &=\pi(i) Q(i, j) \end{aligned} \]
令:
\[ P(i, j)=Q(i, j) \alpha(i, j) \]
\(\alpha\)称为接受率,类似上面提到的接受-拒绝采样中的接受率,在接受-拒绝采样中,接受率调节的是从易抽样分布中得到的样本是否接受其成为目标分布的样本,而在这里,接受率调节服从Q的状态转移是否接受成为P的状态转移。这里的状态转移矩阵P就是分布\(\pi(x)\)对应的马尔可夫链的转移概率矩阵P。即满足细致平稳条的马尔可夫链的转移概率矩阵P可通过接受率的调节,从一个具有普通的转移概率矩阵Q的马尔可夫链变换得到。
这样,就得到了MCMC采样的一般过程:
1) 确定目标分布\(\pi(x)\),
2)设定收敛前的转移次数\(n_1\), 所需样本数\(n_2\). 选定一个马尔可夫链的概率转移矩阵Q,只需马尔可夫链非周期,各状态之间相互连通即可。
3)从简单分布如均匀分布中采样得到初始样本\(x_0\),
4) loop: i from 0 到 \(n_1+n_2 -1\):
- 根据条件概率\(Q(x|x_i)\) 得到 x';
- 从[0,1]的均匀分布中抽样得到 \(\mu\);
- 如果 \(\mu \lt \alpha(x_i,x') = \pi(x')Q(x',x_i)\):
- \(x_{i+1} = x'\),即接受 \(x_i\)到\(x'\)的转移,
- 否则,不接受转移:
- \(x_{i+1} = x_i\)
5) 收集样本\(\{x_{n_1},x_{n_1+1},...,.x_{n_1+n_2}\}\),即为平称分布\(\pi(x)\)的样本集。
此方法对离散、连续情形均适用。
可见,上述方法非常的强大,适用范围很广,但实际应用过程中发现,上述过程收敛很慢,要将\(n_1\)设置的非常大,且设定比较困难,而且收敛过慢,不但耗时且浪费计算资源。这个问题由Metropolis 与 Hastings 解决,并产生了Metropolis-Hastings算法(或称M-H算法)。
M-H 算法
MCMC采样效率低的原因是接受率通常比较小,导致大部分状态转移不被接受。比如上面过程中\(\alpha(x_i,x' ) = 0.1\),那么\(\mu\lt \alpha(x_i,x')\)的概率就只有0.1。优化上述问题的关键在于提高接受率。在细致平稳条件中:
\[ \pi(i) Q(i, j) \alpha(i, j)=\pi(j) Q(j, i) \alpha(j, i) \]
两边同时乘一个系数如 k,等式仍是成立的:
\[ \pi(i) Q(i, j) \alpha(i, j)\cdot k=\pi(j) Q(j, i) \alpha(j, i)\cdot k \]
如果令:
\[ \alpha'(i,j) = \alpha(i,j)\cdot k\\ \alpha'(j,i) = \alpha(j,i)\cdot k \]
成为新的接受率,且\(k\gt 1\), 那么这个接受率在不违背细致平稳条件的情况下被放大了!因为接受率不大于1,放大接受率的上限为1,那不妨让\(\alpha'(i,j), \alpha'(j,i)\) 中较大的为1,这样算法抽样的效率达到最高。即:
\[ \alpha'(i, j)=\min \left\{\frac{\pi(j) Q(j, i)}{\pi(i) Q(i, j)}, 1\right\} \]
这样,就得到了M-H采样算法的一般过程,与MCMC基本一致,只是\(\mu\)的接受空间变大了:
1) 确定目标分布\(\pi(x)\),
2)设定收敛前的转移次数\(n_1\), 所需样本数\(n_2\). 选定一个马尔可夫链的概率转移矩阵Q,只需马尔可夫链非周期,各状态之间相互连通即可。
3)从简单分布如均匀分布中采样得到初始样本\(x_0\),
4) loop: i from 0 到 \(n_1+n_2 -1\):
- 根据条件概率\(Q(x|x_i)\) 得到 x';
- 从[0,1]的均匀分布中抽样得到 \(\mu\);
- 如果 \(\mu \lt \alpha(x_i,x') =\min \left\{\frac{\pi(x') Q(x', x_i)}{\pi(x_i) Q(x_i, x')}, 1\right\}\):
- \(x_{i+1} = x'\),即接受 \(x_i\)到\(x'\)的转移,
- 否则,不接受转移:
- \(x_{i+1} = x_i\)
5) 收集样本\(\{x_{n_1},x_{n_1+1},...,.x_{n_1+n_2}\}\),即为平称分布\(\pi(x)\)的样本集。
Gibbs Sampling
对于高维数据,上述的M-H算法再次突显出了弊端。对于高维数据,联两数据的联合分布会变得很复杂,甚至无法求解;另外,接受率的存在,计算接受率,并在其限制下接受样本,都使得很多算力浪费,效率不高。于是Gibbs进一步提出了Gibbs采样算法。当维度大于1时,不妨先从二维数据开始探讨。设两个点\(A(x_1,y_1),B(x_1,y_2)\), 服从概率分布\(p(x)\). 这两个点的第一维度坐标相同,可推出:
\[ \begin{array}{l}{p\left(x_{1}, y_{1}\right) p\left(y_{2} | x_{1}\right)=p\left(x_{1}\right) p\left(y_{1} | x_{1}\right) p\left(y_{2} | x_{1}\right)} \\ {p\left(x_{1}, y_{2}\right) p\left(y_{1} | x_{1}\right)=p\left(x_{1}\right) p\left(y_{2} | x_{1}\right) p\left(y_{1} | x_{1}\right)}\end{array} \]
进而:
\[ p\left(x_{1}, y_{1}\right) p\left(y_{2} | x_{1}\right)=p\left(x_{1}, y_{2}\right) p\left(y_{1} | x_{1}\right) \]
也就是:
\[ p(A) p\left(y_{2} | x_{1}\right)=p(B) p\left(y_{1} | x_{1}\right) \]
可见当其x维度相同时,两个点在条件概率\(p(y|x)\)作为转移概率的情况下是满足细致平稳条件的。同理,如果有一点\(C(x_2,y_1)\), 那么点\(A,C\)满足细致平稳条件:
\[ p(x_1,y_1)p(x_2|y_1) = p(x_1,y_1)p(x_2,y_1)p(y_1) = p(x_2,y_1)p(x_1|y_1) \\ \]
即:
\[ p(A)p(x_2|y_1) = p(C)p(x_1|y_1) \]
因此对于二维数据的Gibbs采样:
确定目标分布 \(\pi(x_1,x_2)\), 并状态转移次数\(n_1\)与样本个数\(n_2\);
- 随机初始化状态值\(x_1^0,x_2^0\),
- loop(0, \(n_1+n_2\)):
- 从条件概率分布\(P(x_2|x_1^t)\)中采样得到\(x_2^{t+1}\);
- 从条件概率分布P(x_1|x_2^{t+1})中采样得到样本\(x_1^{t+1}\)
上述循环得到的\(\left\{\left(x_{1}^{\left(n_{1}\right)}, x_{2}^{\left(n_{1}\right)}\right),\left(x_{1}^{\left(n_{1}+1\right)}, x_{2}^{\left(n_{1}+1\right)}\right), \dots,\left(x_{1}^{\left(n_{1}+n_{2}-1\right)}, x_{2}^{\left(n_{1}+n_{2}-1\right)}\right)\right\}\) 样本即为所需样本。
这个公式很容易推广到 n 维数据,在n-1个维度固定的情况下,所选维度上的转换是服从细致平稳条件的,n维Gibbs采样过程:
确定目标分布 \(\pi(x_1,x_2, ...,x_n)\), 并状态转移次数\(n_1\)与样本个数\(n_2\);
- 随机初始化状态值\(x_1^0,x_2^0,...,x_n^0\)
- loop(0, \(n_1+n_2\)):
- 从条件概率分布\(P(x_1|x_2^t,x_3^t,...,x_n^t)\)中采样得到$x_1^{t+1} $;
- 从条件概率分布\(P(x_2|x_1^{t+1},x_3^t,...,x_n^t)\)中采样得到样本$x_2^{t+1} $;
- ...
- 从条件概率分布\(P(x_j|x_1^{t+1},x_2^{t+1},...,x_{j-1}^{t+1},x_{j+1}^t,...,x_n^t)\)中采样得到样本\(x_j^{t+1}\);
- ...
- 从条件概率分布\(P(x_n|x_1^{t+1},x_2^{t+1},...,x_{n-1}^{t+1})\)中采样得到样本\(x_n^{t+1}\).
上述循环得到的\(\left\{\left(x_{1}^{\left(n_{1}\right)}, x_{2}^{\left(n_{1}\right)}, \dots, x_{n}^{\left(n_{1}\right)}\right), \ldots,\left(x_{1}^{\left(n_{1}+n_{2}-1\right)}, x_{2}^{\left(n_{1}+n_{2}-1\right)}, \ldots, x_{n}^{\left(n_{1}+n_{2}-1\right)}\right)\right\}\) 样本即为所需样本。