F函数的极大极大算法

F函数中的F应该是（free energy）的缩写，这个函数可以帮我们换一个思路理解EM算法：
EM算法中总有一个Q函数，在证明过程中有一些地方不是很形象，如果用F函数极大极大算法可以比较好的理解。本文所用的变量名称与李航第九章相同，即，隐变量数据：Z；观测变量数据：Y（永远是已知的）；需要估计的模型参数$\theta$,概率分布一律用P（·）表示。

1、最大似然估计法

大致的意思是说，我们现在想知道一个分布，通过在这个陌生的分布里采样的方法来确定这个分布。我们大致想用一些模型来近似这个陌生的分布，我们当然可以很武断的认为这个陌生的分布就是一个确定的分布，比如说是一个的高斯分布，这时候我们需要确定的参数只有$\mu$和$\sigma$假设我们用$\theta$来代表这两个参数。我们从分布中采样，采样的观测数据不妨设为Y，这时候我们如何确定参数$\theta$呢？θ=arg⁡max⁡θ P(Y∣θ)\theta=\mathop{\arg\max}_{\theta} \ \mathrm{P} (Y|\theta)θ=argmaxθ​ P(Y∣θ)或者是θ=arg⁡max⁡θ log(P(Y∣θ))\theta=\mathop{\arg\max}_{\theta} \ log\left(\mathrm{P} (Y|\theta)\right)θ=argmaxθ​ log(P(Y∣θ))也就是我们最大化$P(Y|\theta )$是通过找到这样的参数，使得在由这个参数所确定的分布中，最大可能采样到我们采样出来的结果Y。不难看出，无论怎样只要我们认定了一种高斯分布，无论输入什么样的数据总能得到一组结果，这是好事。但是我们一旦认定了我们希望求出的分布是由一种高斯分布决定的，那么我们所有的运算过程算的再好所能表达的也只有由一个高斯分布所能表达，真实的分布可能千奇百怪，但我们一旦选定这种表达框架，我们得出的结果永远都是高斯分布那种“钟型”的样子，以上是所谓最大似然估计法。

2、EM算法

现在的问题是，如果真实的分布比较复杂，不是一个高斯分布可以描述的了，真实的分布是有90%概率是高斯分布1，有10%概率是高斯分布2，我们可能需要一些隐变量Z来描述关于逼近的关系，【之所以用隐变量，也是希望我们所设定的表达框架表达能力更强一些，比如上面这个例子，隐变量的值就是（10%和90%）】。那么这样我们就需要用到EM算法。无论是最大似然估计还是EM算法，我们都是用这个式子来确定我们想要得到的参数的θ=arg⁡max⁡θL(θ)=arg⁡max⁡θ log(P(Y∣θ))\theta=\mathop{\arg\max}_{\theta} L(\theta)=\mathop{\arg\max}_{\theta}\ log\left(\mathrm{P} (Y|\theta)\right)θ=argmaxθ​L(θ)=argmaxθ​ log(P(Y∣θ))

如果我们采用迭代的方法只要保证找到一个θi\theta^{i}θi的序列，使得一次比一次的log(P(Y∣θi))log\left(\mathrm{P} (Y|\theta^{i})\right)log(P(Y∣θi))大就好了，然后根据李航书上159页的一顿推导可以推出来$L(\theta )$的一个下界函数B(θ,θi)B(\theta,\theta^{i})B(θ,θi)的表达式，如果每一次迭代都能使得这个下界函数往上走一点，也许可以逼近问题的局部最优解。
但是就像李航书上这张图9.1这样画的，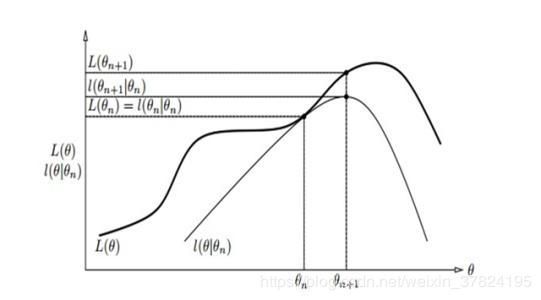

每次只把下界函数往上推不一定能推导局部最优解啊比如B函数如果真的像这幅图一样到θi+1\theta^{i+1}θi+1好像就不行了，但是原书中9.2定理表明，在满足一定条件下其实这种方法总能收敛到一个$L(\theta )$的稳定点。

到这里缕一下，我们想要求的是$logP(Y|\theta )$的最大，但是我们只知道Y，求解过程中还有Z在捣乱，EM的思想在于我先假定知道一个固定的θi\theta_iθi​假如当前的θi\theta_iθi​是一个比较不错的值，我先找一个关于隐变量Z的分布P~(Z)\tilde{P}(Z)P~(Z)（E步），这个分布与当前θi\theta_iθi​值有关，同时也与$\theta$变量有关，然后调整$\theta$值使得那个函数最大化（M步）出来了一个新的$\theta$进行下一次迭代。仔细看李航书上的推导花一些时间不难理解，但是如果看了F函数极大极大，简直就太好理解了。

3、F函数

关于EM的内容有很多博客说的都很好，以下结合了李航老师的书，The Elements of Statistical Learning和Neal, R. M., & Hinton, G. E. (1998). A View of the Em Algorithm that Justifies Incremental, Sparse, and other Variants. Learning in Graphical Models, 355–368.说一下F函数极大极大。

最开始的时候不是很理解，看了The Elements of Statistical Learning里的这幅图后突然懂了一些，下图中横坐标是隐变量，纵坐标是需要估计的模型参数$\theta$，红线一会儿解释。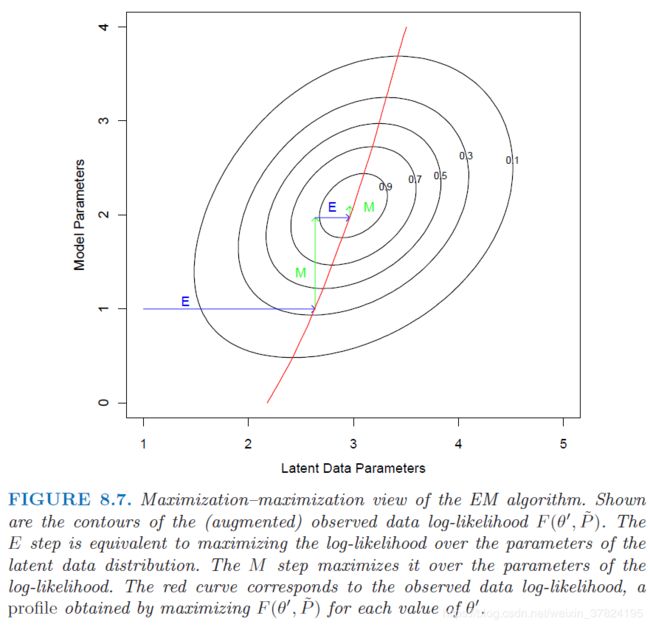

其实EM算法或者F函数极大极大就是对

1.需要估计的模型参数$\theta$
2.观测不到的参数$Z$

进行调整的过程，F函数相当于把这两步骤融合在了一个函数里，对这两个($\theta$和$Z$)固定其中一个调整另一个，F函数的形式可以写成F(P~(Z),θ)=EP~(Z)[logP(Y,Z∣θ)]−EP~(Z)[logP~(Z)]F(\tilde{P}(Z),\theta)=E_{\tilde{P}(Z)}[logP(Y,Z|\theta)]-E_{\tilde{P}(Z)}[log\tilde{P}(Z)]F(P~(Z),θ)=EP~(Z)​[logP(Y,Z∣θ)]−EP~(Z)​[logP~(Z)]

固定$\theta$------第一个极大：根据166页引理9.1发现固定$\theta$的话关于$Z$分布求极值可以有一个比较好的闭式解即P~(Z)=P(Z∣Y,θ)\tilde{P}(Z)=P(Z|Y,\theta)P~(Z)=P(Z∣Y,θ)，其中我们可以把上面的图中的红色的线理解成$P(Z|Y,\theta )$，那么对于固定的$\theta$也就是上图中E的部分我们向右寻找最佳的隐变量（其实是隐变量的分布）使得当前的Fθ(P~(Z))F_{\theta}(\tilde{P}(Z))Fθ​(P~(Z))函数取得极大，而这个极大正好取在$P(Z|Y,\theta )$这个点上。

固定P~(Z)\tilde{P}(Z)P~(Z)------第二个极大：然后让我们感到幸福的地方在于当我们把P~(Z)\tilde{P}(Z)P~(Z)设为$P(Z|Y,\theta )$后我们的终极目标$log\left(\mathrm{P}(Y|\theta )\right)$正好等于F函数，而且屏蔽了隐变量（虽然这时候我们当前对于隐变量的估计不一定准确，但是这就可以很光明正大的优化这个F函数了，对于隐变量估计的不准确可以下一次迭代的时候再说），那么第二个极大就是极大参数$\theta$了。F函数有两项，第二项EP~(Z)[logP~(Z)]E_{\tilde{P}(Z)}[log\tilde{P}(Z)]EP~(Z)​[logP~(Z)]与参数的选取没有关系，只与隐变量的分布有关，那么我们确定了隐变量分布以后通过最大化F函数求参数就只剩下了第一项，

比较有意思的是优化第一项所能算出的结果与就与之前EM算法中的通过优化Q函数算出来的结果一样了！！当然，F函数和Q函数在计算结果上应该是一样的，所以自然也有理论保证迭代会收敛到一个局部最优解（定理9.3）。

当然在实际计算的时候可以有各种策略，比如GEM3算法可以每次迭代的时候少更新一些维度的$\theta$