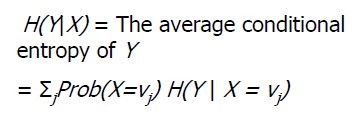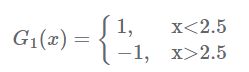数据挖掘常用模型
决策树
转载于:http://www.cnblogs.com/pinard/p/6050306.html (楼主总结的很好,就拿来主义了,不顾以后还是多像楼主学习)
决策树算法在机器学习中算是很经典的一个算法系列了。它既可以作为分类算法,也可以作为回归算法,同时也特别适合集成学习比如随机森林。本文就对决策树算法原理做一个总结,上篇对ID3, C4.5的算法思想做了总结,下篇重点对CART算法做一个详细的介绍。决策树根据一步步地属性分类可以将整个特征空间进行划分,从而区别出不同的分类样本
1. 决策树ID3算法的信息论基础
机器学习算法其实很古老,作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过,有这么多条件,用哪个条件特征先做if,哪个条件特征后做if比较优呢?怎么准确的定量选择这个标准就是决策树机器学习算法的关键了。1970年代,一个叫昆兰的大牛找到了用信息论中的熵来度量决策树的决策选择过程,方法一出,它的简洁和高效就引起了轰动,昆兰把这个算法叫做ID3。下面我们就看看ID3算法是怎么选择特征的。
首先,我们需要熟悉信息论中熵的概念。熵度量了事物的不确定性,越不确定的事物,它的熵就越大。具体的,随机变量X的熵的表达式如下:
H(X)=−∑i=1npilogpiH(X)=−∑i=1npilogpi
其中n代表X的n种不同的离散取值。而pipi代表了X取值为i的概率,log为以2或者e为底的对数。举个例子,比如X有2个可能的取值,而这两个取值各为1/2时X的熵最大,此时X具有最大的不确定性。值为H(X)=−(12log12+12log12)=log2H(X)=−(12log12+12log12)=log2。如果一个值概率大于1/2,另一个值概率小于1/2,则不确定性减少,对应的熵也会减少。比如一个概率1/3,一个概率2/3,则对应熵为H(X)=−(13log13+23log23)=log3−23log2 熟悉了一个变量X的熵,很容易推广到多个个变量的联合熵,这里给出两个变量X和Y的联合熵表达式: H(X,Y)=−∑i=1np(xi,yi)logp(xi,yi)H(X,Y)=−∑i=1np(xi,yi)logp(xi,yi) 有了联合熵,又可以得到条件熵的表达式H(X|Y),条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下: H(X|Y)=−∑i=1np(xi,yi)logp(xi|yi)=∑j=1np(yj)H(X|yj)H(X|Y)=−∑i=1np(xi,yi)logp(xi|yi)=∑j=1np(yj)H(X|yj) 好吧,绕了一大圈,终于可以重新回到ID3算法了。我们刚才提到H(X)度量了X的不确定性,条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性,那么H(X)-H(X|Y)呢?从上面的描述大家可以看出,它度量了X在知道Y以后不确定性减少程度,这个度量我们在信息论中称为互信息,,记为I(X,Y)。在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大,则越适合用来分类。 上面一堆概念,大家估计比较晕,用下面这个图很容易明白他们的关系。左边的椭圆代表H(X),右边的椭圆代表H(Y),中间重合的部分就是我们的互信息或者信息增益I(X,Y), 左边的椭圆去掉重合部分就是H(X|Y),右边的椭圆去掉重合部分就是H(Y|X)。两个椭圆的并就是H(X,Y)。 1、 信息熵:H(X) 描述X携带的信息量。 信息量越大(值变化越多),则越不确定,越不容易被预测。 对于抛硬币问题,每次有2种情况,信息熵为1 对于投骰子问题,每次有6中情况,信息熵为1.75 下面为公式: 其中log2(p)可以理解为p这个需要用几个bit位表示。如p(x1)=1/2, p(x2)=1/4, p(x3)=1/8, p(x4)=1/8, 可以用x1: 1, x2: 10, x3: 110, x4: 111表示,因为为了让平均的bit位最少,概率越大的bit为设的越短。而-log2(p)正好对应bit位数。 那么H(X)可以理解为比特位的期望值。 信息熵特点:(以概率和为1为前提哈) a) 不同类别的概率分布越均匀,信息熵越大; b) 类别个数越多,信息熵越大; c) 信息熵越大,越不容易被预测;(变化个数多,变化之间区分小,则越不容易被预测)(对于确定性问题,信息熵为0;p=1; E=p*logp=0) 2、 信息增益IG(Y|X): 衡量一个属性(x)区分样本(y)的能力。 当新增一个属性(x)时,信息熵H(Y)的变化大小即为信息增益。 IG(Y|X)越大表示x越重要。 条件熵:H(Y|X),当X条件下Y的信息熵 信息增益: IG(Y|X)=H(Y)-H(Y|X) 熵(entropy):在信息论和概率统计中,熵是表示随机变量不确定性的度量 条件熵(conditional entropy):表示在一直随机变量X的条件下随机变量Y的不确定性度量。 信息增益(information gain):信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。 信息增益比(information gain ratio):其信息增益g(D, A)与训练数据集D关于特征A的值的熵HA(D)之比 基尼指数(gini index):基尼指数Gini(D)表示集合D的不确定性,基尼指数越大,样本集合的不确定性也就越大,这一点与熵相似。 上面提到ID3算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树,用计算出的信息增益最大的特征来建立决策树的当前节点。这里我们举一个信息增益计算的具体的例子。比如我们有15个样本D,输出为0或者1。其中有9个输出为0, 6个输出为1。 样本中有个特征A,取值为A1,A2和A3。在取值为A1的样本的输出中,有3个输出为1, 2个输出为0,取值为A2的样本输出中,2个输出为1,3个输出为0, 在取值为A3的样本中,4个输出为1,1个输出为0. 样本D的熵为: H(D)=−(915log2915+615log2615)=0.971H(D)=−(915log2915+615log2615)=0.971 样本D在特征下的条件熵为: H(D|A)=515H(D1)+515H(D2)+515H(D3)H(D|A)=515H(D1)+515H(D2)+515H(D3) =−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888=−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888 对应的信息增益为 I(D,A)=H(D)−H(D|A)=0.083I(D,A)=H(D)−H(D|A)=0.083 下面我们看看具体算法过程大概是怎么样的。 输入的是m个样本,样本输出集合为D,每个样本有n个离散特征,特征集合即为A,输出为决策树T。 算法的过程为: 1)初始化信息增益的阈值ϵϵ 2)判断样本是否为同一类输出DiDi,如果是则返回单节点树T。标记类别为DiDi 3) 判断特征是否为空,如果是则返回单节点树T,标记类别为样本中输出类别D实例数最多的类别。 4)计算A中的各个特征(一共n个)对输出D的信息增益,选择信息增益最大的特征AgAg 5) 如果AgAg的信息增益小于阈值ϵϵ,则返回单节点树T,标记类别为样本中输出类别D实例数最多的类别。 6)否则,按特征AgAg的不同取值AgiAgi将对应的样本输出D分成不同的类别DiDi。每个类别产生一个子节点。对应特征值为AgiAgi。返回增加了节点的数T。 7)对于所有的子节点,令D=Di,A=A−{Ag}D=Di,A=A−{Ag}递归调用2-6步,得到子树TiTi并返回。 ID3算法虽然提出了新思路,但是还是有很多值得改进的地方。 a)ID3没有考虑连续特征,比如长度,密度都是连续值,无法在ID3运用。这大大限制了ID3的用途。 b)ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现,在相同条件下,取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值,各为1/2,另一个变量为3个值,各为1/3,其实他们都是完全不确定的变量,但是取3个值的比取2个值的信息增益大。如果校正这个问题呢? c) ID3算法对于缺失值的情况没有做考虑 d) 没有考虑过拟合的问题 ID3 算法的作者昆兰基于上述不足,对ID3算法做了改进,这就是C4.5算法,也许你会问,为什么不叫ID4,ID5之类的名字呢?那是因为决策树太火爆,他的ID3一出来,别人二次创新,很快 就占了ID4, ID5,所以他另辟蹊径,取名C4.0算法,后来的进化版为C4.5算法。下面我们就来聊下C4.5算法 上一节我们讲到ID3算法有四个主要的不足,一是不能处理连续特征,第二个就是用信息增益作为标准容易偏向于取值较多的特征,最后两个是缺失值处理的问和过拟合问题。昆兰在C4.5算法中改进了上述4个问题。 对于第一个问题,不能处理连续特征, C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个,从小到大排列为a1,a2,...,ama1,a2,...,am,则C4.5取相邻两样本值的中位数,一共取得m-1个划分点,其中第i个划分点Ti表示Ti表示为:Ti=ai+ai+12Ti=ai+ai+12。对于这m-1个点,分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为atat,则小于atat的值为类别1,大于atat的值为类别2,这样我们就做到了连续特征的离散化。要注意的是,与离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。 对于第二个问题,信息增益作为标准容易偏向于取值较多的特征的问题。我们引入一个信息增益比的变量IR(X,Y)IR(X,Y),它是信息增益和特征熵的比值。表达式如下: IR(D,A)=I(A,D)HA(D)IR(D,A)=I(A,D)HA(D) 其中D为样本特征输出的集合,A为样本特征,对于特征熵HA(D)HA(D), 表达式如下: HA(D)=−∑i=1n|Di||D|log2|Di||D|HA(D)=−∑i=1n|Di||D|log2|Di||D| 其中n为特征A的类别数, DiDi为特征A的第i个取值对应的样本个数。D为样本个数。 特征数越多的特征对应的特征熵越大,它作为分母,可以校正信息增益容易偏向于取值较多的特征的问题。 对于第三个缺失值处理的问题,主要需要解决的是两个问题,一是在样本某些特征缺失的情况下选择划分的属性,二是选定了划分属性,对于在该属性上缺失特征的样本的处理。 对于第一个子问题,对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分,对每个样本设置一个权重(初始可以都为1),然后划分数据,一部分是有特征值A的数据D1,另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比,最后乘上一个系数,这个系数是无特征A缺失的样本加权后所占加权总样本的比例。 对于第二个子问题,可以将缺失特征的样本同时划分入所有的子节点,不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1,特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1,A2,A3。对应权重调节为2/9,3/9, 4/9。 对于第4个问题,C4.5引入了正则化系数进行初步的剪枝。具体方法这里不讨论。下篇讲CART的时候会详细讨论剪枝的思路。 除了上面的4点,C4.5和ID的思路区别不大。 C4.5虽然改进或者改善了ID3算法的几个主要的问题,仍然有优化的空间。 1)由于决策树算法非常容易过拟合,因此对于生成的决策树必须要进行剪枝。剪枝的算法有非常多,C4.5的剪枝方法有优化的空间。思路主要是两种,一种是预剪枝,即在生成决策树的时候就决定是否剪枝。另一个是后剪枝,即先生成决策树,再通过交叉验证来剪枝。后面在下篇讲CART树的时候我们会专门讲决策树的剪枝思路,主要采用的是后剪枝加上交叉验证选择最合适的决策树。 2)C4.5生成的是多叉树,即一个父节点可以有多个节点。很多时候,在计算机中二叉树模型会比多叉树运算效率高。如果采用二叉树,可以提高效率。 3)C4.5只能用于分类,如果能将决策树用于回归的话可以扩大它的使用范围。 4)C4.5由于使用了熵模型,里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算。如果能够加以模型简化可以减少运算强度但又不牺牲太多准确性的话,那就更好了。 这4个问题在CART树里面部分加以了改进。所以目前如果不考虑集成学习话,在普通的决策树算法里,CART算法算是比较优的算法了。scikit-learn的决策树使用的也是CART算法。 对于C4.5算法,我们也提到了它的不足,比如模型是用较为复杂的熵来度量,使用了相对较为复杂的多叉树,只能处理分类不能处理回归等。对于这些问题, CART算法大部分做了改进。CART算法也就是我们下面的重点了。由于CART算法可以做回归,也可以做分类,我们分别加以介绍,先从CART分类树算法开始,重点比较和C4.5算法的不同点。接着介绍CART回归树算法,重点介绍和CART分类树的不同点。然后我们讨论CART树的建树算法和剪枝算法,最后总结决策树算法的优缺点。 我们知道,在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。 具体的,在分类问题中,假设有K个类别,第k个类别的概率为pkpk, 则基尼系数的表达式为: Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kp2kGini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2 如果是二类分类问题,计算就更加简单了,如果属于第一个样本输出的概率是p,则基尼系数的表达式为: Gini(p)=2p(1−p)Gini(p)=2p(1−p) 对于个给定的样本D,假设有K个类别, 第k个类别的数量为CkCk,则样本D的基尼系数表达式为: Gini(D)=1−∑k=1K(|Ck||D|)2Gini(D)=1−∑k=1K(|Ck||D|)2 特别的,对于样本D,如果根据特征A的某个值a,把D分成D1和D2两部分,则在特征A的条件下,D的基尼系数表达式为: Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2)Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2) 大家可以比较下基尼系数表达式和熵模型的表达式,二次运算是不是比对数简单很多?尤其是二类分类的计算,更加简单。但是简单归简单,和熵模型的度量方式比,基尼系数对应的误差有多大呢?对于二类分类,基尼系数和熵之半的曲线如下: 从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算,二可以建立一个更加优雅的二叉树模型。 对于CART分类树连续值的处理问题,其思想和C4.5是相同的,都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同,C4.5使用的是信息增益,则CART分类树使用的是基尼系数。 具体的思路如下,比如m个样本的连续特征A有m个,从小到大排列为a1,a2,...,ama1,a2,...,am,则CART算法取相邻两样本值的中位数,一共取得m-1个划分点,其中第i个划分点Ti表示Ti表示为:Ti=ai+ai+12Ti=ai+ai+12。对于这m-1个点,分别计算以该点作为二元分类点时的基尼系数。选择基尼系数最小的点作为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为atat,则小于atat的值为类别1,大于atat的值为类别2,这样我们就做到了连续特征的离散化。要注意的是,与离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。 对于CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。 回忆下ID3或者C4.5,如果某个特征A被选取建立决策树节点,如果它有A1,A2,A3三种类别,我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同,他采用的是不停的二分,还是这个例子,CART分类树会考虑把A分成{A1}和{A2,A3}{A1}和{A2,A3}, {A2}和{A1,A3}{A2}和{A1,A3}, {A3}和{A1,A2}{A3}和{A1,A2}三种情况,找到基尼系数最小的组合,比如{A2}和{A1,A3}{A2}和{A1,A3},然后建立二叉树节点,一个节点是A2对应的样本,另一个节点是{A1,A3}对应的节点。从描述可以看出,如果离散特征A有n个取值,则可能的组合有n(n-1)/2种。同时,由于这次没有把特征A的取值完全分开,后面我们还有机会在子节点继续选择到特征A来划分A1和A3。这和ID3或者C4.5不同,在ID3或者C4.5的一棵子树中,离散特征只会参与一次节点的建立。 上面介绍了CART算法的一些和C4.5不同之处,下面我们看看CART分类树建立算法的具体流程,之所以加上了建立,是因为CART树算法还有独立的剪枝算法这一块,这块我们在第5节讲。 算法输入是训练集D,基尼系数的阈值,样本个数阈值。 输出是决策树T。 我们的算法从根节点开始,用训练集递归的建立CART树。 1) 对于当前节点的数据集为D,如果样本个数小于阈值或者没有特征,则返回决策子树,当前节点停止递归。 2) 计算样本集D的基尼系数,如果基尼系数小于阈值,则返回决策树子树,当前节点停止递归。 3) 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数,对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和上篇的C4.5算法里描述的相同。 4) 在计算出来的各个特征的各个特征值对数据集D的基尼系数中,选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值,把数据集划分成两部分D1和D2,同时建立当前节点的左右节点,做节点的数据集D为D1,右节点的数据集D为D2. 5) 对左右的子节点递归的调用1-4步,生成决策树。 对于生成的决策树做预测的时候,假如测试集里的样本A落到了某个叶子节点,而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。 CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方。 首先,我们要明白,什么是回归树,什么是分类树。两者的区别在于样本输出,如果样本输出是离散值,那么这是一颗分类树。如果果样本输出是连续值,那么那么这是一颗回归树。 除了概念的不同,CART回归树和CART分类树的建立和预测的区别主要有下面两点: 1)连续值的处理方法不同 2)决策树建立后做预测的方式不同。 对于连续值的处理,我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,我们使用了常见的均方差的度量方式,CART回归树的度量目标是,对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为: min⏟A,s[min⏟c1∑xi∈D1(A,s)(yi−c1)2+min⏟c2∑xi∈D2(A,s)(yi−c2)2]min⏟A,s[min⏟c1∑xi∈D1(A,s)(yi−c1)2+min⏟c2∑xi∈D2(A,s)(yi−c2)2] 其中,c1c1为D1数据集的样本输出均值,c2c2为D2数据集的样本输出均值。 对于决策树建立后做预测的方式,上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。 除了上面提到了以外,CART回归树和CART分类树的建立算法和预测没有什么区别。 CART回归树和CART分类树的剪枝策略除了在度量损失的时候一个使用均方差,一个使用基尼系数,算法基本完全一样,这里我们一起来讲。 由于决策时算法很容易对训练集过拟合,而导致泛化能力差,为了解决这个问题,我们需要对CART树进行剪枝,即类似于线性回归的正则化,来增加决策树的返回能力。但是,有很多的剪枝方法,我们应该这么选择呢? CART采用的办法是后剪枝法,即先生成决策树,然后产生所有可能的剪枝后的CART树,然后使用交叉验证来检验各种剪枝的效果,选择泛化能力最好的剪枝策略。 也就是说,CART树的剪枝算法可以概括为两步,第一步是从原始决策树生成各种剪枝效果的决策树,第二部是用交叉验证来检验剪枝后的预测能力,选择泛化预测能力最好的剪枝后的数作为最终的CART树。 首先我们看看剪枝的损失函数度量,在剪枝的过程中,对于任意的一刻子树T,其损失函数为: Cα(Tt)=C(Tt)+α|Tt|Cα(Tt)=C(Tt)+α|Tt| 其中,αα为正则化参数,这和线性回归的正则化一样。C(Tt)C(Tt)为训练数据的预测误差,分类树是用基尼系数度量,回归树是均方差度量。|Tt||Tt|是子树T的叶子节点的数量。 当α=0α=0时,即没有正则化,原始的生成的CART树即为最优子树。当α=∞α=∞时,即正则化强度达到最大,此时由原始的生成的CART树的根节点组成的单节点树为最优子树。当然,这是两种极端情况。一般来说,αα越大,则剪枝剪的越厉害,生成的最优子树相比原生决策树就越偏小。对于固定的αα,一定存在使损失函数Cα(T)Cα(T)最小的唯一子树。 看过剪枝的损失函数度量后,我们再来看看剪枝的思路,对于位于节点t的任意一颗子树TtTt,如果没有剪枝,它的损失是 Cα(Tt)=C(Tt)+α|Tt|Cα(Tt)=C(Tt)+α|Tt| 如果将其剪掉,仅仅保留根节点,则损失是 Cα(T)=C(T)+αCα(T)=C(T)+α 当α=0α=0或者αα很小时,Cα(Tt) Cα(T)=C(T)+αCα(T)=C(T)+α 。当αα继续增大时不等式反向,也就是说,如果满足下式: α=C(T)−C(Tt)|Tt|−1α=C(T)−C(Tt)|Tt|−1 TtTt和TT有相同的损失函数,但是TT节点更少,因此可以对子树TtTt进行剪枝,也就是将它的子节点全部剪掉,变为一个叶子节点TT。 最后我们看看CART树的交叉验证策略。上面我们讲到,可以计算出每个子树是否剪枝的阈值αα,如果我们把所有的节点是否剪枝的值αα都计算出来,然后分别针对不同的αα所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的αα,有了这个αα,我们就可以用对应的最优子树作为最终结果。 好了,有了上面的思路,我们现在来看看CART树的剪枝算法。 输入是CART树建立算法得到的原始决策树TT。 输出是最优决策子树TαTα。 算法过程如下: 1)初始化αmin=∞αmin=∞, 最优子树集合ω={T}ω={T}。 2)从叶子节点开始自下而上计算各内部节点t的训练误差损失函数Cα(Tt)Cα(Tt)(回归树为均方差,分类树为基尼系数), 叶子节点数|Tt||Tt|,以及正则化阈值α=min{C(T)−C(Tt)|Tt|−1,αmin}α=min{C(T)−C(Tt)|Tt|−1,αmin}, 更新αmin=ααmin=α 3) 得到所有节点的αα值的集合M。 4)从M中选择最大的值αkαk,自上而下的访问子树t的内部节点,如果C(T)−C(Tt)|Tt|−1≤αkC(T)−C(Tt)|Tt|−1≤αk时,进行剪枝。并决定叶节点t的值。如果是分类树,则是概率最高的类别,如果是回归树,则是所有样本输出的均值。这样得到αkαk对应的最优子树TkTk 5)最优子树集合ω=ω∪Tkω=ω∪Tk, M=M−{αk}M=M−{αk}。 6) 如果M不为空,则回到步骤4。否则就已经得到了所有的可选最优子树集合ωω. 7) 采用交叉验证在ωω选择最优子树TαTα 上面我们对CART算法做了一个详细的介绍,CART算法相比C4.5算法的分类方法,采用了简化的二叉树模型,同时特征选择采用了近似的基尼系数来简化计算。当然CART树最大的好处是还可以做回归模型,这个C4.5没有。下表给出了ID3,C4.5和CART的一个比较总结。希望可以帮助大家理解。 看起来CART算法高大上,那么CART算法还有没有什么缺点呢?有!主要的缺点我认为如下: 1)应该大家有注意到,无论是ID3, C4.5还是CART,在做特征选择的时候都是选择最优的一个特征来做分类决策,但是大多数,分类决策不应该是由某一个特征决定的,而是应该由一组特征决定的。这样绝息到的决策树更加准确。这个决策树叫做多变量决策树(multi-variate decision tree)。在选择最优特征的时候,多变量决策树不是选择某一个最优特征,而是选择最优的一个特征线性组合来做决策。这个算法的代表是OC1,这里不多介绍。 2)如果样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习里面的随机森林之类的方法解决。 终于到了最后的总结阶段了,这里我们不再纠结于ID3, C4.5和 CART,我们来看看决策树算法作为一个大类别的分类回归算法的优缺点。这部分总结于scikit-learn的英文文档。 首先我们看看决策树算法的优点: 1)简单直观,生成的决策树很直观。 2)基本不需要预处理,不需要提前归一化,处理缺失值。 3)使用决策树预测的代价是O(log2m)O(log2m)。 m为样本数。 4)既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。 5)可以处理多维度输出的分类问题。 6)相比于神经网络之类的黑盒分类模型,决策树在逻辑上可以得到很好的解释 7)可以交叉验证的剪枝来选择模型,从而提高泛化能力。 8) 对于异常点的容错能力好,健壮性高。 我们再看看决策树算法的缺点: 1)决策树算法非常容易过拟合,导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。 2)决策树会因为样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。 3)寻找最优的决策树是一个NP难的问题,我们一般是通过启发式方法,容易陷入局部最优。可以通过集成学习之类的方法来改善。 4)有些比较复杂的关系,决策树很难学习,比如异或。这个就没有办法了,一般这种关系可以换神经网络分类方法来解决。 5)如果某些特征的样本比例过大,生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。 性能良好的决策树的选择标准是什么? 性能良好的决策树的选择标准是一个与训练数据矛盾较小的决策树,同时具有很好的泛化能力。言外之意就是说,好的决策树不仅对训练样本有着很好的分类效果,对于测试集也有着较低的误差率。 ID3、C4.5&CART 其实不同的决策树学习算法只是它们选择特征的依据不同,决策树的生成过程都是一样的(根据当前环境对特征进行贪婪的选择)。 ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征,每一次都选择使得信息增益最大的特征进行分裂,递归地构建决策树。 ID3算法以信息增益作为划分训练数据集的特征,有一个致命的缺点。选择取值比较多的特征往往会具有较大的信息增益,所以ID3偏向于选择取值较多的特征。 针对ID3算法的不足,C4.5算法根据信息增益比来选择特征,对这一问题进行了校正。 CART指的是分类回归树,它既可以用来分类,又可以被用来进行回归。CART用作回归树时用平方误差最小化作为选择特征的准则,用作分类树时采用基尼指数最小化原则,进行特征选择,递归地生成二叉树。 决策树的剪枝:我们知道,决策树在生成的过程中采用了贪婪的方法来选择特征,从而达到对训练数据进行更好地拟合(其实从极端角度来看,决策树对训练集的拟合可以达到零误差)。而决策树的剪枝是为了简化模型的复杂度,防止决策树的过拟合问题。具体的决策树剪枝策略可以参见李航的《统计学习方法》。 集成学习(Ensemble)思想、自助法(bootstrap)与bagging 如果我们有个大小为N的样本,我们希望从中得到m个大小为N的样本用来训练。那么我们可以这样做:首先,在N个样本里随机抽出一个样本x1,然后记下来,放回去,再抽出一个x2,… ,这样重复N次,即可得到N的新样本,这个新样本里可能有重复的。重复m次,就得到了m个这样的样本。实际上就是一个有放回的随机抽样问题。每一个样本在每一次抽的时候有同样的概率(1/N)被抽中。 这个方法在样本比较小的时候很有用,比如我们的样本很小,但是我们希望留出一部分用来做验证,那如果传统方法做train-validation的分割的话,样本就更小了,bias会更大,这是不希望的。而自助法不会降低训练样本的规模,又能留出验证集(因为训练集有重复的,但是这种重复又是随机的),因此有一定的优势。 至于自助法能留出多少验证,或者说,m个样本的每个新样本里比原来的样本少了多少?可以这样计算:每抽一次,任何一个样本没抽中的概率为 (1-1/N),一共抽了N次,所以任何一个样本没进入新样本的概率为(1-1/N)^N。那么从统计意义上来说,就意味着大概有(1-1/N)^N这么大比例的样本作为验证集。当N→inf时,这个值大概是1/e,36.8%。以这些为验证集的方式叫做包外估计(out of bag estimate) bagging的名称来源于 ( B**ootstrap **AGG**regat**ING ),意思是自助抽样集成,这种方法将训练集分成m个新的训练集,然后在每个新训练集上构建一个模型,各自不相干,最后预测时我们将这个m个模型的结果进行整合,得到最终结果。整合方式就是:分类问题用majority voting,回归用均值。 决策树(Decision Tree)与随机森林(Random Forest) 常用的决策树有ID4,C4.5,CART等。在生成树的过程中,需要选择用那个特征进行剖分,一般来说,选取的原则是,分开后能尽可能地提升纯度,可以用信息增益,增益率,以及基尼系数等指标来衡量。如果是一棵树的话,为了避免过拟合,还要进行剪枝(prunning),取消那些可能会导致验证集误差上升的节点。 随机森林实际上是一种特殊的bagging方法,它将决策树用作bagging中的模型。首先,用bootstrap方法生成m个训练集,然后,对于每个训练集,构造一颗决策树,在节点找特征进行分裂的时候,并不是对所有特征找到能使得指标(如信息增益)最大的,而是在特征中随机抽取一部分特征,在抽到的特征中间找到最优解,应用于节点,进行分裂。随机森林的方法由于有了bagging,也就是集成的思想在,实际上相当于对于样本和特征都进行了采样(如果把训练数据看成矩阵,就像实际中常见的那样,那么就是一个行和列都进行采样的过程),所以可以避免过拟合。 prediction阶段的方法就是bagging的策略,分类投票,回归均值。 K-Means算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用很广泛。K-Means算法有大量的变体,本文就从最传统的K-Means算法讲起,在其基础上讲述K-Means的优化变体方法。包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。 K-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。 如果用数据表达式表示,假设簇划分为,则我们的目标是最小化平方误差E: 其中是簇的均值向量,有时也称为质心,表达式为: 如果我们想直接求上式的最小值并不容易,这是一个NP难的问题,因此只能采用启发式的迭代方法。 K-Means采用的启发式方式很简单,用下面一组图就可以形象的描述。 上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。 当然在实际K-Mean算法中,我们一般会多次运行图c和图d,才能达到最终的比较优的类别。 在上一节我们对K-Means的原理做了初步的探讨,这里我们对K-Means的算法做一个总结。 首先我们看看K-Means算法的一些要点。 1)对于K-Means算法,首先要注意的是k值的选择,一般来说,我们会根据对数据的先验经验选择一个合适的k值,如果没有什么先验知识,则可以通过交叉验证选择一个合适的k值。 2)在确定了k的个数后,我们需要选择k个初始化的质心,就像上图b中的随机质心。由于我们是启发式方法,k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心,最好这些质心不能太近。 好了,现在我们来总结下传统的K-Means算法流程。 输入是样本集,聚类的簇树k,最大迭代次数N 输出是簇划分 1) 从数据集D中随机选择k个样本作为初始的k个质心向量: 2)对于n=1,2,...,N a) 将簇划分C初始化为 b) 对于i=1,2...m,计算样本和各个质心向量的距离:,将标记最小的为所对应的类别。此时更新 c) 对于j=1,2,...,k,对中所有的样本点重新计算新的质心 e) 如果所有的k个质心向量都没有发生变化,则转到步骤3) 3) 输出簇划分 在上节我们提到,k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。 K-Means++的对于初始化质心的优化策略也很简单,如下: a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心 在传统的K-Means算法中,我们在每轮迭代时,要计算所有的样本点到所有的质心的距离,这样会比较的耗时。那么,对于距离的计算有没有能够简化的地方呢?elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。那么哪些距离不需要计算呢? elkan K-Means利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算。 第一种规律是对于一个样本点和两个质心。如果我们预先计算出了这两个质心之间的距离,则如果计算发现,我们立即就可以知道。此时我们不需要再计算,也就是说省了一步距离计算。 第二种规律是对于一个样本点和两个质心。我们可以得到。这个从三角形的性质也很容易得到。 利用上边的两个规律,elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的,有缺失值的话,这个方法就不使用了,此时某些距离无法计算,则不能使用该算法。 在统的K-Means算法中,要计算所有的样本点到所有的质心的距离。如果样本量非常大,比如达到10万以上,特征有100以上,此时用传统的K-Means算法非常的耗时,就算加上elkan K-Means优化也依旧。在大数据时代,这样的场景越来越多。此时Mini Batch K-Means应运而生。 顾名思义,Mini Batch,也就是用样本集中的一部分的样本来做传统的K-Means,这样可以避免样本量太大时的计算难题,算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。 在Mini Batch K-Means中,我们会选择一个合适的批样本大小batch size,我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的?一般是通过无放回的随机采样得到的。 为了增加算法的准确性,我们一般会多跑几次Mini Batch K-Means算法,用得到不同的随机采样集来得到聚类簇,选择其中最优的聚类簇。 初学者很容易把K-Means和KNN搞混,两者其实差别还是很大的。 K-Means是无监督学习的聚类算法,没有样本输出;而KNN是监督学习的分类算法,有对应的类别输出。KNN基本不需要训练,对测试集里面的点,只需要找到在训练集中最近的k个点,用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程,找到k个类别的最佳质心,从而决定样本的簇类别。 当然,两者也有一些相似点,两个算法都包含一个过程,即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。 K-Means是个简单实用的聚类算法,这里对K-Means的优缺点做一个总结。 K-Means的主要优点有: 1)原理比较简单,实现也是很容易,收敛速度快。 2)聚类效果较优。 3)算法的可解释度比较强。 4)主要需要调参的参数仅仅是簇数k。 K-Means的主要缺点有: 1)K值的选取不好把握(改进:可以通过在一开始给定一个适合的数值给k,通过一次K-means算法得到一次聚类中心。对于得到的聚类中心,根据得到的k个聚类的距离情况,合并距离最近的类,因此聚类中心数减小,当将其用于下次聚类时,相应的聚类数目也减小了,最终得到合适数目的聚类数。可以通过一个评判值E来确定聚类数得到一个合适的位置停下来,而不继续合并聚类中心。重复上述循环,直至评判函数收敛为止,最终得到较优聚类数的聚类结果)。 2)对于不是凸的数据集比较难收敛(改进:基于密度的聚类算法更加适合,比如DESCAN算法) 3)如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。 4) 采用迭代方法,得到的结果只是局部最优。 5) 对噪音和异常点比较的敏感(改进1:离群点检测的LOF算法,通过去除离群点后再聚类,可以减少离群点和孤立点对于聚类效果的影响;改进2:改成求点的中位数,这种聚类方式即K-Mediods聚类(K中值))。 6)初始聚类中心的选择(改进1:k-means++;改进2:二分K-means,相关知识详见这里和这里)。 支持向量机(Support Vector Machine,常简称为SVM)是一种监督式学习的方法,可广泛地应用于统计分类以及回归分析。它是将向量映射到一个更高维的空间里,在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面,分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大,分类器的总误差越小。 从分类或回归的角度来看,SVM的分类只考虑分类面附近的局部的点,即支持向量,而诸如Logistic回归的算法要考虑全部样本的点,基于所有数据点的分布情况来构建分类边界。那么如何理解SVM这种依靠超平面与支持向量进行分类或回归的问题?在这里我们基于二维平面的9个简单场景来深入理解其工作原理。 图1:何谓正确的超平面? image.png 如上图,A、B、C三个超平面,对星形与圆形标志进行划分,很明显,超平面B是正确的超平面。 图2-3:何谓最优的超平面? image.png 图4:SVM得到的有时候并不是最优分类超平面 image.png 如上图,根据我们前边的边距最大原则,B是SVM算法得到的最优超平面,但是从实际来看,A才是能够将两类完全区分开的超平面,所以,SVM得到的有时候并不是最优分类超平面,那么我们就要怀疑SVM算法的可行性吗?我们可以从下一幅图找到答案。 图5-6:线性不可分下的最优超平面 image.png 如上图,这两类无法用一条直线去划分,基于SVM的边距最大化原则,我们得到的最优超平面只能是这样的: image.png 结合图4以及图5-6的内容,可以看到有时候SVM不能完全将两类很好地分开,但是我们仍然觉得它是比较好的分类器,这是因为我们训练的样本中有些数据本来就是噪声,存在异常值,如果我们在训练(学习)的时候把这些错误的点学习到了,那么模型在下次碰到这些错误情况的时候就难免出错了。这种学习的时候学到了“噪声”的过程就是一个过拟合(over-fitting),这在机器学习中是一个大忌,而SVM在拟合时会保证一定的容错性,忽略异常值而考虑全局性的类别分布,就像图4、5、6所示的那样。 图7-9:非线性分类下的SVM image.png 如上图,两个类之间不能有线性超平面,那么SVM如何对这两个类进行分类?之前我们构建分类函数为f(x) = w.x + b(w.x表示w与x的内积),这里就需要我们可以让空间从原本的线性空间变成一个更高维的空间,在这个高维的线性空间下,再用一个超平面进行划分。 image.png image.png 许多商业企业在日复一日的运营中积聚了大量的交易数据。例如,超市的收银台每天都收集大量的顾客购物数据。例如,下表给出了一个这种数据集的例子,我们通常称其为购物篮交易(market basket transaction)。表中每一行对应一个交易,包含一个唯一标识TID和特定顾客购买的商品集合。零售商对分析这些数据很感兴趣,以便了解其顾客的购买行为。可以使用这种有价值的信息来支持各种商业中的实际应用,如市场促销,库存管理和顾客关系管理等等。 令I={i1,i2,⋯,id}是购物篮数据中所有项的集合,而T={t1,t2,⋯,tN}是所有交易的集合。包含0个或多个项的集合被称为项集(itemset)。如果一个项集包含k个项,则称它为 k-项集。显然,每个交易ti包含的项集都是I的子集。 例如考虑规则{Milk, Diaper}→{Beer},则易得: Association Rule Mining Task:Given a set of transactions T, the goal of association rule mining is to find all rules having: 频繁项集产生:其目标是发现满足最小支持度阈值的所有项集,这些项集称作频繁项集(frequent itemset)。 最容易想到、也最直接的进行关联关系挖掘的方法或许就是暴力搜索(Brute-force)的方法: 然而,由于Brute-force的计算量过大,所以采样这种方法并不现实!格结构(Lattice structure)常被用来枚举所有可能的项集。如下图所示为I={a,b,c,d,e} 发现频繁项集的一种原始方法是确定格结构中每个候选项集(candidate itemset)的支持度计 数。为了完成这一任务,必须将每个候选项集与每个交易进行比较,如下图所示。如果候选项集包含在交易中,则候选项集的支持度计数增加。例如,由于项集{Bread, Milk}出现在事务1、4 和5中,其支持度计数将增加3次。这种方法的开销可能非常大,因为它需要进行O(NMw)次比 较,其中N是交易数,M=2^k−1是候选项集数,而w是交易的最大宽度(也就是交易中最大的项数)。 在上一小节的末尾,我们已经看到Brute-force在实际中并不可取。我们必须设法降低产生频繁项集的计算复杂度。此时我们可以利用支持度对候选项集进行剪枝,这也是Apriori所利用的第一条先验原理: R. Agrawal 和 R. Srikant于1994年在文献【2】中提出了Apriori算法,该算法的描述如下: 或者在其他资料上更为常见的是下面这种形式化的描述(注意这跟前面的文字描述是一致的): 下面是一个具体的例子,最开始数据库里有4条交易,{A、C、D},{B、C、E},{A、B、C、E},{B、E},使用min_support=2作为支持度阈值,最后我们筛选出来的频繁集为{B、C、E}。 上述例子中,最值得我们从L2到C3的这一步。这其实就是在执行伪代码中第一个蓝色框条所标注的地方:Ck+1=GenerateCandidates(Lk),具体来说在Apriori算法中,它所使用的策略如下: 写一点自己理解的AdaBoost,然后再贴上面试过程中被问到的相关问题。按照以下目录展开。 当然,也可以去我的博客上看 AdaBoost是典型的Boosting算法,属于Boosting家族的一员。在说AdaBoost之前,先说说Boosting提升算法。Boosting算法是将“弱学习算法“提升为“强学习算法”的过程,主要思想是“三个臭皮匠顶个诸葛亮”。一般来说,找到弱学习算法要相对容易一些,然后通过反复学习得到一系列弱分类器,组合这些弱分类器得到一个强分类器。Boosting算法要涉及到两个部分,加法模型和前向分步算法。加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下: FM(x;P)=∑m=1nβmh(x;am)FM(x;P)=∑m=1nβmh(x;am) 其中,h(x;am)h(x;am) 就是一个个的弱分类器,amam是弱分类器学习到的最优参数,βmβm就是弱学习在强分类器中所占比重,PP是所有amam和βmβm的组合。这些弱分类器线性相加组成强分类器。 前向分步就是说在训练过程中,下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式: Fm(x)=Fm−1(x)+βmhm(x;am)Fm(x)=Fm−1(x)+βmhm(x;am) 由于采用的损失函数不同,Boosting算法也因此有了不同的类型,AdaBoost就是损失函数为指数损失的Boosting算法。 基于Boosting的理解,对于AdaBoost,我们要搞清楚两点: 对于第一个问题,AdaBoost改变了训练数据的权值,也就是样本的概率分布,其思想是将关注点放在被错误分类的样本上,减小上一轮被正确分类的样本权值,提高那些被错误分类的样本权值。然后,再根据所采用的一些基本机器学习算法进行学习,比如逻辑回归。 对于第二个问题,AdaBoost采用加权多数表决的方法,加大分类误差率小的弱分类器的权重,减小分类误差率大的弱分类器的权重。这个很好理解,正确率高分得好的弱分类器在强分类器中当然应该有较大的发言权。 为了加深理解,我们来举一个例子。 有如下的训练样本,我们需要构建强分类器对其进行分类。x是特征,y是标签。 令权值分布D1=(w1,1,w1,2,…,w1,10)D1=(w1,1,w1,2,…,w1,10) 并假设一开始的权值分布是均匀分布:w1,i=0.1,i=1,2,…,10w1,i=0.1,i=1,2,…,10 现在开始训练第一个弱分类器。我们发现阈值取2.5时分类误差率最低,得到弱分类器为: 当然,也可以用别的弱分类器,只要误差率最低即可。这里为了方便,用了分段函数。得到了分类误差率e1=0.3e1=0.3。 第二步计算(G1(x)(G1(x)在强分类器中的系数α1=12log1−e1e1=0.4236α1=12log1−e1e1=0.4236,这个公式先放在这里,下面再做推导。 第三步更新样本的权值分布,用于下一轮迭代训练。由公式: w2,i=w1,iz1exp(−α1yiG1(xi)),i=1,2,…,10w2,i=w1,iz1exp(−α1yiG1(xi)),i=1,2,…,10 得到新的权值分布,从各0.1变成了: D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)D2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715) 可以看出,被分类正确的样本权值减小了,被错误分类的样本权值提高了。 第四步得到第一轮迭代的强分类器: sign(F1(x))=sign(0.4236G1(x))sign(F1(x))=sign(0.4236G1(x)) 以此类推,经过第二轮……第N轮,迭代多次直至得到最终的强分类器。迭代范围可以自己定义,比如限定收敛阈值,分类误差率小于某一个值就停止迭代,比如限定迭代次数,迭代1000次停止。这里数据简单,在第3轮迭代时,得到强分类器: sign(F3(x))=sign(0.4236G1(x)+0.6496G2(x)+0.7514G3(x))sign(F3(x))=sign(0.4236G1(x)+0.6496G2(x)+0.7514G3(x)) F(x)=sign(F3(x))F(x)=sign(F3(x))就是最终的强分类器。 总结一下,得到AdaBoost的算法流程: em=∑i=1Nwm,iI(Gm(xi)≠yi)em=∑i=1Nwm,iI(Gm(xi)≠yi) αm=12log1−ememαm=12log1−emem wm+1,i=wm,izmexp(−αmyiGm(xi)),i=1,2,…,10wm+1,i=wm,izmexp(−αmyiGm(xi)),i=1,2,…,10 zm=∑i=1Nwm,iexp(−αmyiGm(xi))zm=∑i=1Nwm,iexp(−αmyiGm(xi)) F(x)=sign(∑i=1NαmGm(x))F(x)=sign(∑i=1NαmGm(x)) 现在我们来搞清楚上述公式是怎么来的。 假设已经经过m−1m−1轮迭代,得到Fm−1(x)Fm−1(x),根据前向分步,我们可以得到: Fm(x)=Fm−1(x)+αmGm(x)Fm(x)=Fm−1(x)+αmGm(x) 我们已经知道AdaBoost是采用指数损失,由此可以得到损失函数: Loss=∑i=1Nexp(−yiFm(xi))=∑i=1Nexp(−yi(Fm−1(xi)+αmGm(xi)))Loss=∑i=1Nexp(−yiFm(xi))=∑i=1Nexp(−yi(Fm−1(xi)+αmGm(xi))) 这时候,Fm−1(x)Fm−1(x)是已知的,可以作为常量移到前面去: Loss=∑i=1Nwm,i˜exp(−yiαmGm(xi))Loss=∑i=1Nwm,i~exp(−yiαmGm(xi)) 是不是觉得还不够像?那就再化简一下: wm,i˜=exp(−yi(Fm−1(xi)+αm−1Gm−1(xi)))=wm−1,i˜exp(−yiαm−1Gm−1(xi))wm,i~=exp(−yi(Fm−1(xi)+αm−1Gm−1(xi)))=wm−1,i~exp(−yiαm−1Gm−1(xi)) 现在够像了吧?ok,我们继续化简Loss: Loss=∑yi=Gm(xi)wm,i˜exp(−αm)+∑yi≠Gm(xi)wm,i˜exp(αm)Loss=∑yi=Gm(xi)wm,i~exp(−αm)+∑yi≠Gm(xi)wm,i~exp(αm) =∑i=1Nwm,i˜(∑yi=Gm(xi)wm,i˜∑Ni=1wm,i˜exp(−αm)+∑yi≠Gm(xi)wm,i˜∑Ni=1wm,i˜exp(αm))=∑i=1Nwm,i~(∑yi=Gm(xi)wm,i~∑i=1Nwm,i~exp(−αm)+∑yi≠Gm(xi)wm,i~∑i=1Nwm,i~exp(αm)) 公式变形之后,炒鸡激动!∑yi≠Gm(xi)wm,i˜∑Ni=1wm,i˜∑yi≠Gm(xi)wm,i~∑i=1Nwm,i~这个不就是分类误差率emem吗???!重写一下, Loss=∑i=1Nwm,i˜exp(−αm)+emexp(αm))Loss=∑i=1Nwm,i~exp(−αm)+emexp(αm)) Ok,这样我们就得到了化简之后的损失函数。接下来就是求导了。 对αmαm求偏导,令∂Loss∂αm=0∂Loss∂αm=0得到: αm=12log1−ememαm=12log1−emem 真漂亮! 另外,AdaBoost的代码实战与详解请戳代码实战之AdaBoost 今年8月开始找工作,参加大厂面试问到的相关问题有如下几点: 最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来,当测试对象的属性和某个训练对象的属性完全匹配时,便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢,其次就是存在一个测试对象同时与多个训练对象匹配,导致一个训练对象被分到了多个类的问题,基于这些问题呢,就产生了KNN。 KNN是通过测量不同特征值之间的距离进行分类。它的的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。K通常是不大于20的整数。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 下面通过一个简单的例子说明一下:如下图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 由此也说明了KNN算法的结果很大程度取决于K的选择。 在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,在这里距离一般使用欧氏距离或曼哈顿距离: 同时,KNN通过依据k个对象中占优的类别进行决策,而不是单一的对象类别决策。这两点就是KNN算法的优势。 接下来对KNN算法的思想总结一下:就是在训练集中数据和标签已知的情况下,输入测试数据,将测试数据的特征与训练集中对应的特征进行相互比较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类,其算法的描述为: 1)计算测试数据与各个训练数据之间的距离; 2)按照距离的递增关系进行排序; 3)选取距离最小的K个点; 4)确定前K个点所在类别的出现频率; 5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。 1、优点 简单,易于理解,易于实现,无需估计参数,无需训练 适合对稀有事件进行分类(例如当流失率很低时,比如低于0.5%,构造流失预测模型) 特别适合于多分类问题(multi-modal,对象具有多个类别标签),例如根据基因特征来判断其功能分类,kNN比SVM的表现要好 2、缺点 懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢 可解释性较差,无法给出决策树那样的规则。 1、k值设定为多大? k太小,分类结果易受噪声点影响;k太大,近邻中又可能包含太多的其它类别的点。(对距离加权,可以降低k值设定的影响) k值通常是采用交叉检验来确定(以k=1为基准) 经验规则:k一般低于训练样本数的平方根 2、类别如何判定最合适? 投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法更恰当一些。 3、如何选择合适的距离衡量? 高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。 变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行标准化。 4、训练样本是否要一视同仁? 在训练集中,有些样本可能是更值得依赖的。 可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。 5、性能问题? kNN是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找k个近邻)。 懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并计算距离。 已经有一些方法提高计算的效率,例如压缩训练样本量等。 6、能否大幅减少训练样本量,同时又保持分类精度? 浓缩技术(condensing) 编辑技术(editing) 对地形进行分类 knn.py prep_terrain_data.py 训练数据分布图 测试数据分类结果及决策面 计算结果 朴素贝叶斯法是在假设输入向量x的特征条件独立(即在输入模式所属类别确定时,输入向量x的每个元素取值互不影响)下,通过样本集合学习输入x与输出y的联合概率分布。再用所得到的联合概率分布通过贝叶斯公式计算条件概率 https://blog.csdn.net/xiaoyi_eric/article/details/80274938 Sklearn 是基于Python的机器学习工具模块。里面主要包含了6大模块:分类、回归、聚类、降维、模型选择、预处理。 根据Sklearn 官方文档资料,下面将各个模块中常用的模型函数总结出来。 1. 回归及分类(监督学习) 1.1 广义线性模型 (fromsklearn import linear_model) 最小二乘法:拟合一个线性模型, 使得数据集实际观测数据和预测数据(估计值)之间残差平方和最小。 clf=linear_model.LinearRegression(), clf.fit(X,y) 岭回归:改良的最小二乘,解决共线问题。 clf=linear_model.Ridge(alpha=0.5),clf.fit(X,y) 逻辑回归: clf=linear_model.LogisticRegression() 1.2 朴素贝叶斯 高斯模型: from sklearn.naive_bayes import GassianNB Gnb=GassianNB(),gnb.fit(data, target).predict(data) 多项式模型:MultinomialNB 伯努利模型:会把输入数据二元化BernoulliNB 1.3 决策树 from sklearn import tree 决策树分类器:clf=tree.DecisionTreeClassifier() 回归分类器(y 值为float非int): clf=tree. DecisionTreeRegressor() 1.4 支持向量机 from sklearn import svm clf=svm.SVC() 2. 聚类 K-means: from sklearn.cluster import KMeans kmeans= KMeans(n_clusters=2, random_state=0).fit(X) 3. 降维 PCA: From sklearn.decomposition import PCA pca = PCA(n_components=2) method: fit(X[y]) get_covariance() get_params([deep]) get_precision() score(X[y]) 4. 特征选择 树特征: From sklearn.ensemble import ExtraTreesClassifier 5 .数据预处理 From sklearn import preprocessing 标准化:preprocessing.scale(x) 规范化:preprocessing.normalize() 二值化: preprocessing.Binarizer() 处理缺失值:fromsklearn.preprocessing import Imputer imp=Imputer(missing_values='NaN',strategy='mean',axis=0)![]()
信息熵(Entropy)、信息增益(Information Gain)概念解释
2. 决策树ID3算法的思路
3. 决策树ID3算法的不足
4. 决策树C4.5算法的改进
5. 决策树C4.5算法的不足与思考
1. CART分类树算法的最优特征选择方法
![]()
2. CART分类树算法对于连续特征和离散特征处理的改进
3. CART分类树建立算法的具体流程
4. CART回归树建立算法
5. CART树算法的剪枝
6. CART算法小结
算法
支持模型
树结构
特征选择
连续值处理
缺失值处理
剪枝
ID3
分类
多叉树
信息增益
不支持
不支持
不支持
C4.5
分类
多叉树
信息增益比
支持
支持
支持
CART
分类,回归
二叉树
基尼系数,均方差
支持
支持
支持
7. 决策树算法小结
集成学习(ensemble)思想是为了解决单个模型或者某一组参数的模型所固有的缺陷,从而整合起更多的模型,取长补短,避免局限性。随机森林就是集成学习思想下的产物,将许多棵决策树整合成森林,并合起来用来预测最终结果。
首先,介绍自助法(bootstrap),这个奇怪的名字来源于文学作品 The Adventures of Baron Munchausen(吹牛大王历险记),这个作品中的一个角色用提着自己鞋带的方法把自己从湖底下提了上来。因此采用意译的方式,叫做自助法。自助法顾名思义,是这样一种方法:即从样本自身中再生成很多可用的同等规模的新样本,从自己中产生和自己类似的,所以叫做自助,即不借助其他样本数据。自助法的具体含义如下:
bagging和boosting是集成学习两大阵营,之后在总结两者的异同。
决策树是用树的结构来构建分类模型,每个节点代表着一个属性,根据这个属性的划分,进入这个节点的儿子节点,直至叶子节点,每个叶子节点都表征着一定的类别,从而达到分类的目的。
K-Means
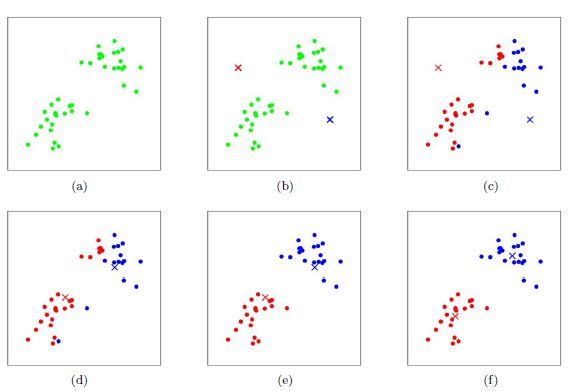
1. K-Means原理初探
2. 传统K-Means算法流程
3. K-Means初始化优化K-Means++
b) 对于数据集中的每一个点,计算它与已选择的聚类中心中最近聚类中心的距离
c) 选择一个新的数据点作为新的聚类中心,选择的原则是:较大的点,被选取作为聚类中心的概率较大
d) 重复b和c直到选择出k个聚类质心
e) 利用这k个质心来作为初始化质心去运行标准的K-Means算法4. K-Means距离计算优化elkan K-Means
5. 大样本优化Mini Batch K-Means
6. K-Means与KNN
7. K-Means小结
SVM
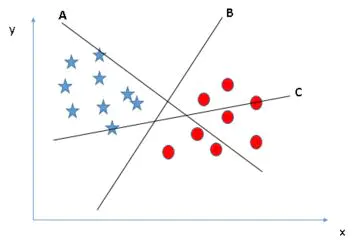
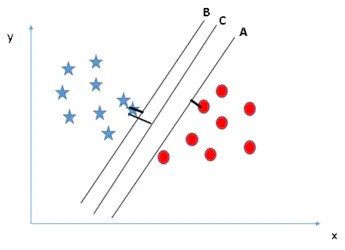
如下图,A、B、C三个超平面均能对星形与圆形标志进行划分,哪个是最优的?
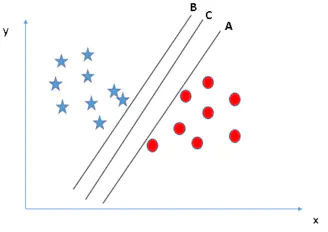
如下图,最优分类平面的条件是使间隔最大化。我们通过任一类(星形或圆形标志)与超平面距离最近的点,基于其与超平面距离的最大化来判定最优超平面,这个距离称为边距(Margin)。相比较于A、B,超平面C的边距最大,且具有鲁棒性,也就是说与任一类别的边距都最大,而不像A、B泛化性较差。
注意:这里不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。
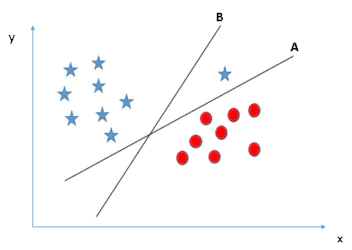
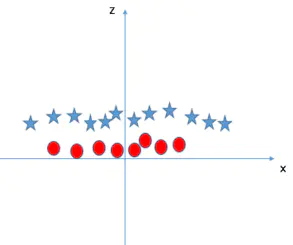
我们构建新特征z = x^2 + y^2,然后在x、z轴上绘制样本点,可以看到如何去有效分类这两种类别。这就是增加了一个新的维度,在高维空间划分两类。SVM有一种称为核函数的技术。这些函数采用低维输入空间并将其转换为更高维空间,即将不可分离问题转换为可分离问题,这些函数称为内核。它主要用于非线性分离问题。
总结:
从上面9幅图可以知道SVM的工作原理:边距最大化;忽略异常值;采用核函数来处理非线性的情况。需要注意的是,上面是对SVM简单场景的分析,实际的SVM工作原理相对复杂。
Apriori算法
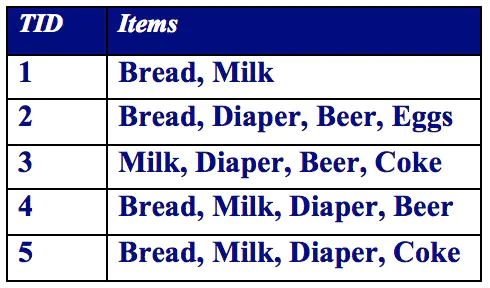
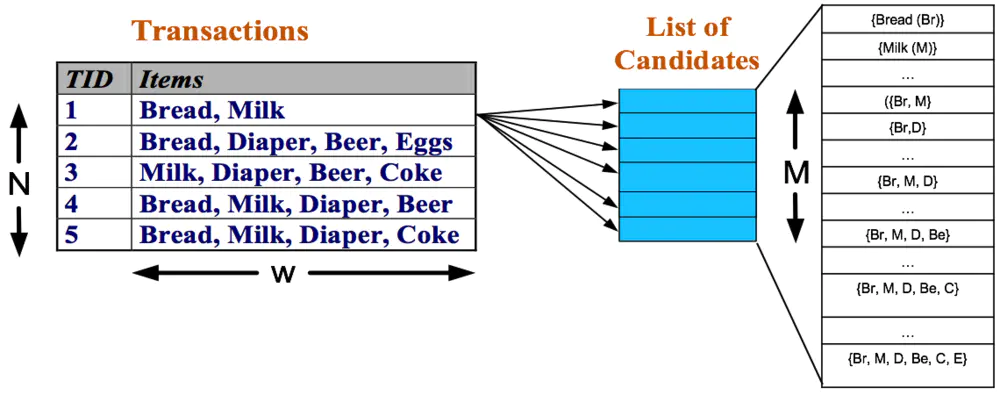
关联规则是形如 X→Y 的蕴涵表达式,其中X和Y是不相交的项集,即 X∩Y=∅。关联规则的强度可以用它的支持度(support)和置信度(confidence)来度量。支持度确定规则可以用于给定数据集的频繁程度,而置信度确定Y在包含X的交易中出现的频繁程度。支持度(s:Fraction of transactions that contain both X and Y)和置信度(c:How often items in Y appear in transactions that contain X)这两种度量的形式定义如下:
1)support ≥ minsup threshold
2)confidence ≥ minconf threshold
因此,大多数关联规则挖掘算法通常采用的一种策略是,将关联规则挖掘任务分解为如下两个主要的子任务。
规则的产生:其目标是从上一步发现的频繁项集中提取所有高置信度的规则,这些规则称作强规则(strong rule)。
通常,频繁项集产生所需的计算开销远大于产生规则所需的计算开销。
1)List all possible association rules
2)Compute the support and confidence for each rule
3)Prune rules that fail the minsup and minconf thresholds
的项集格。一般来说,排除空集后,一个包含k
个项的数据集可能产生2k−1
个频繁项集。由于在实际应用中k
的值可能非常大,需要探查的项集搜索空集可能是指数规模的。3、先验原理
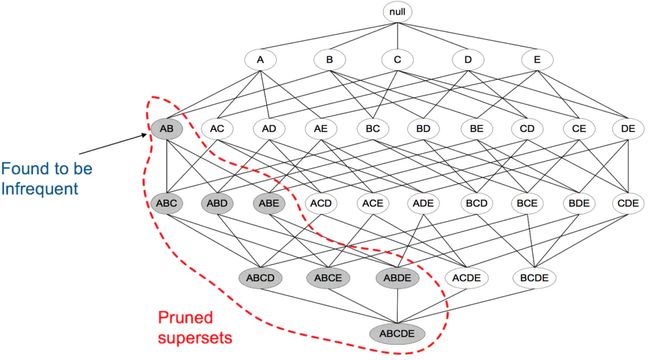
Apriori定律1:如果一个集合是频繁项集,则它的所有子集都是频繁项集。
例如:假设一个集合{A,B}是频繁项集,即A、B同时出现在一条记录的次数大于等于最小支持度min_support,则它的子集{A},{B}出现次数必定大于等于min_support,即它的子集都是频繁项集。
Apriori定律2:如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
举例:假设集合{A}不是频繁项集,即A出现的次数小于 min_support,则它的任何超集如{A,B}出现的次数必定小于min_support,因此其超集必定也不是频繁项集。
下图表示当我们发现{A,B}是非频繁集时,就代表所有包含它的超级也是非频繁的,即可以将它们都剪除。4、Apriori算法
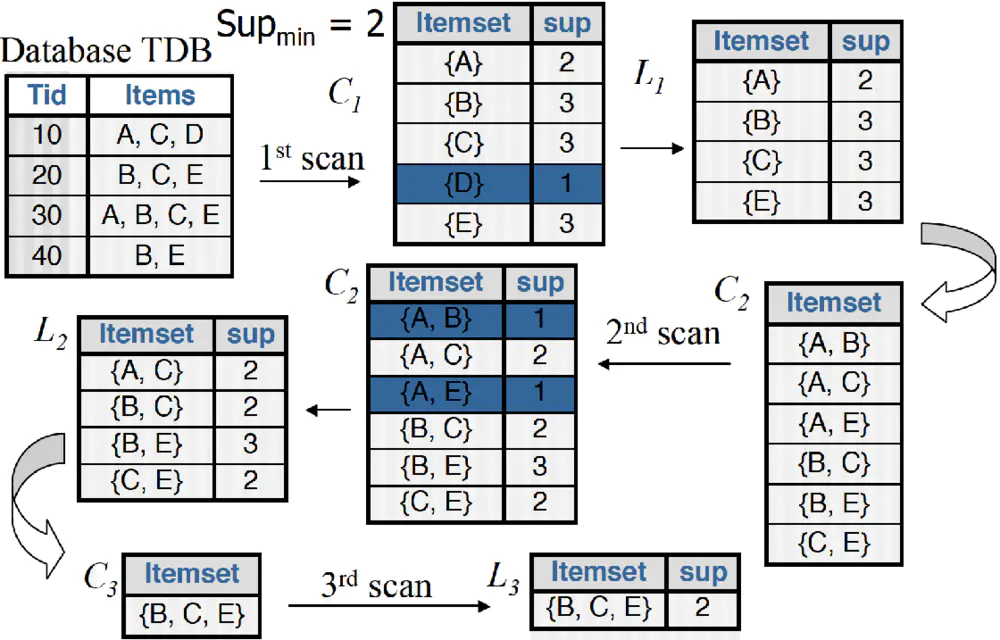
5、实例介绍
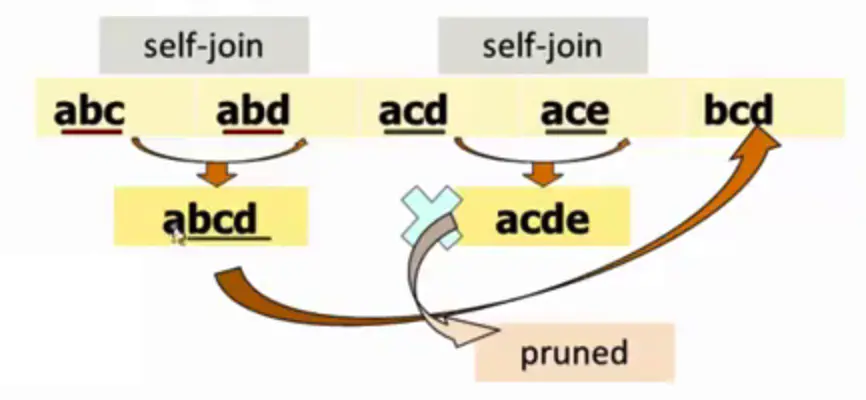
可见生成策略由两部分组成,首先是self-joining部分。例如,假设我们有一个L3={abc, abd, acd, ace, bcd}(注意这已经是排好序的}。选择两个itemsets,它们满足条件:前k-1个item都相同,但最后一个item不同,把它们组成一个新的Ck+1的项集。如下图所示,{abc}和{abd}组成{abcd},{acd}和{ace}组成{acde}。生成策略的第二部分是pruning。对于一个位于Ck+1中的项集c,s是c的大小为k的子集,如果s不存在于Lk中,则将c从Ck+1中删除。如下图所示,因为{acde}的子集{cde}并不存在于L3中,所以我们将{acde}从C4中删除。最后得到的C4,仅包含一个项集{abcd}。
回到之前的例子,从L2到C3的这一步,我们就只能获得{B、C、E}。以上便是Apriori算法的最核心思想。当然在具体实现的时候,如何Count Supports of Candidates也是需要考虑的问题,我们这里略去这部分内容的讨论。
Adaboost
Boosting提升算法
AdaBoost
原理理解
实例
序号
1
2
3
4
5
6
7
8
9
10
x
0
1
2
3
4
5
6
7
8
9
y
1
1
1
-1
-1
-1
1
1
1
-1
的分类误差率为0,结束迭代。算法流程
公式推导
其中,wm,i˜=exp(−yi(Fm−1(x)))wm,i~=exp(−yi(Fm−1(x))) ,敲黑板!这个就是每轮迭代的样本权重!依赖于前一轮的迭代重分配。
面经
KNN
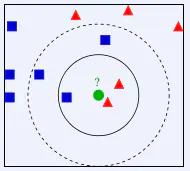
K-近邻算法(KNN)概述
优缺点
常见问题
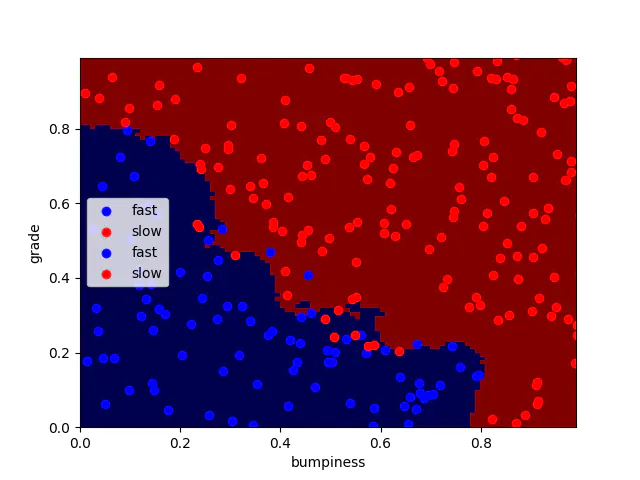
使用 sklearn 进行算法使用
#!/usr/bin/python
import matplotlib.pyplot as plt
from prep_terrain_data import makeTerrainData
from class_vis import prettyPicture
from time import time
features_train, labels_train, features_test, labels_test = makeTerrainData()
### the training data (features_train, labels_train) have both "fast" and "slow"
### points mixed together--separate them so we can give them different colors
### in the scatterplot and identify them visually
grade_fast = [features_train[ii][0] for ii in range(0, len(features_train)) if labels_train[ii]==0]
bumpy_fast = [features_train[ii][1] for ii in range(0, len(features_train)) if labels_train[ii]==0]
grade_slow = [features_train[ii][0] for ii in range(0, len(features_train)) if labels_train[ii]==1]
bumpy_slow = [features_train[ii][1] for ii in range(0, len(features_train)) if labels_train[ii]==1]
#### initial visualization
plt.xlim(0.0, 1.0)
plt.ylim(0.0, 1.0)
plt.scatter(bumpy_fast, grade_fast, color = "b", label="fast")
plt.scatter(grade_slow, bumpy_slow, color = "r", label="slow")
plt.legend()
plt.xlabel("bumpiness")
plt.ylabel("grade")
plt.show()
################################################################################
### your code here! name your classifier object clf if you want the
### visualization code (prettyPicture) to show you the decision boundary
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=10,weights='distance')
t0 = time()
clf.fit(features_train,labels_train)
print "training time : " ,round(time()-t0,3),"s"
t1 = time()
pred = clf.predict(features_test)
print "predicting time : " ,round(time()-t1,3),"s"
from sklearn.metrics import accuracy_score
acc = accuracy_score(pred,labels_test)
print 'accuracy_score :',acc
try:
prettyPicture(clf, features_test, labels_test)
except NameError:
pass
#!/usr/bin/python
import random
def makeTerrainData(n_points=1000):
###############################################################################
### make the toy dataset
random.seed(42)
grade = [random.random() for ii in range(0,n_points)]
bumpy = [random.random() for ii in range(0,n_points)]
error = [random.random() for ii in range(0,n_points)]
y = [round(grade[ii]*bumpy[ii]+0.3+0.1*error[ii]) for ii in range(0,n_points)]
for ii in range(0, len(y)):
if grade[ii]>0.8 or bumpy[ii]>0.8:
y[ii] = 1.0
### split into train/test sets
X = [[gg, ss] for gg, ss in zip(grade, bumpy)]
split = int(0.75*n_points)
X_train = X[0:split]
X_test = X[split:]
y_train = y[0:split]
y_test = y[split:]
grade_sig = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==0]
bumpy_sig = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==0]
grade_bkg = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==1]
bumpy_bkg = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==1]
training_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig}
, "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}}
grade_sig = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==0]
bumpy_sig = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==0]
grade_bkg = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==1]
bumpy_bkg = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==1]
test_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig}
, "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}}
return X_train, y_train, X_test, y_test
training time : 0.002 s
predicting time : 0.005 s
accuracy_score : 0.94
朴素贝叶斯
![]() (后验概率)。将输入模式分类到后验概率最大的一个类别中。
(后验概率)。将输入模式分类到后验概率最大的一个类别中。
EM算法
Sklearn库