数据分析学习总结笔记07:方差分析
数据分析学习总结笔记07:方差分析
- 1 方差分析概述
- 1.1 方差分析简介
- 1.2 方差分析基本思想和原理
- 1.3 方差分析的基本假设
- 2 单因素方差分析(One-way ANOVA)
- 2.1 单因素方差分析概念
- 2.2 单因素方差分析的原理
- 2.3 单因素方差分析的基本假设
- 3 双因素方差分析(Two-way ANOVA)
- 3.1 无交互作用的双因素方差分析
- 3.2 有交互作用的双因素方差分析
- 4 方差分析实践操作
- 4.1 Excel
- 4.2 SPSS
- 4.3 R语言
1 方差分析概述
1.1 方差分析简介
方差分析(analysis of variance,ANOVA)最早由英国统计学家R. A. Fisher 提出,主要用于两个及两个以上样本均数差别的显著性检验。通过检验多个总体均值是否相等来判断是否有显著影响,即通过分析数据的误差判断各总体均值是否相等。
- 特点:方差分析可同时分析多个样本,提高检验效率;将所有信息结合在一起,增加了分析的可靠性。
1.2 方差分析基本思想和原理
方差分析的基本思想和原理基于两类误差。也就是随机误差和系统误差1。
• 随机误差——因子的同一处理(总体)下, 样本各观察值之间的差异,这种差异可以看成是随机因素的影响, 称为随机误差。
• 系统误差——因子的不同处理(不同总体)下, 各观察值之间的差异,这种差异可能是由于抽样的随机性所造成的, 也可能是由于行业本身所造成的,后者所形成的误差是由系统性因素造成的, 称为系统误差。
所以方差分析的实质是——比较两类误差,以检验均值是否相等;比较的基础是方差比;如果系统(处理)误差明显地不同于随机误差,则均值就是不相等的;反之,均值就是相等的。这里数据的误差用平方和(sum of squares)表示。
• 组内平方和(Within Groups)——因子的同一处理(同一个总体)下样本数据的平方和。组内平方和只包含随机误差。
• 组间平方和(Between Groups)——因子的不同处理(不同总体)下各样本之间的平方和。组间平方和既包括随机误差, 也包括系统误差。
- 若原假设成立, 组间平方和与组内平方和经过平均后的数值就应该很接近, 它们的比值就会接近1。
- 若原假设不成立, 组间平方和平均后的数值就会大于组内平方和平均后的数值, 它们之间的比值就会大于1。当这个比值大到某种程度时, 就可以说不同处理之间存在着显著差异, 也就是自变量对因变量有影响。
1.3 方差分析的基本假设
(1)各总体的方差必须相等(方差齐性):各组观察数据是从具有相同方差的总体中抽取的(Bartlett检验/Levene检验/Flinger-Killeen检验)。
(2)各总体必须服从正态分布:对于因子的每一个处理, 其观察值是来自服从正态分布总体的简单随机样本(Shapiro检验)。
(3)各观测值相互独立(可以通过控制抽样过程来控制独立性,无具体的检验方法)。
2 单因素方差分析(One-way ANOVA)
2.1 单因素方差分析概念
单因素方差分析主要用于研究定性变量或定序变量(自变量)与定量变量(因变量)之间的关系。影响因素变量的取值被称为影响因素的水平2。
- 目的:分析不同影响因素水平下,因变量是否有显著差异,即影响因素的不同水平是否对因变量产生了显著影响。
- 应用举例:
- 分析不同施肥量是否给农作物带来显著影响;
- 考察地区差异是否会影响妇女的生育率;
- 研究学历对工资收入的影响。
2.2 单因素方差分析的原理
单因素方差分析是通过比较各个类别的组内差异和类别之间的组间差异大小来确定变量之间是否相关。
- 如果组内差异大,组间差异小,则说明两个变量之间不相关;
- 如果组间差异大,组内差异小,则说明两个变量之间相关。
2.3 单因素方差分析的基本假设
(1)独立:各组数据相互独立,互不相关;
(2)正态:各组数据服从正态分布;
(3)方差齐性:各组方差相等。
3 双因素方差分析(Two-way ANOVA)
3.1 无交互作用的双因素方差分析
有的时候,因变量可能受到来自一个以上的因素的影响,最典型的就是双因素方差分析。假如因素A与因素B没有联合效应,则称为无交互作用的双因素方差分析。
- 举例:假如某经销商想知道一款饮料的销售额与销售地点和饮料包装风格的关系,探究这两个因素是否都在影响销售额或者只有一个因素影响销售额。
3.2 有交互作用的双因素方差分析
因素之间的交互作用在现实中很常见,比如胖胖的人喜欢蓝色的衣服,南方的人更喜欢喝雪花啤酒等,前者是体重和颜色的交互作用,后者是地区和啤酒品牌的交互作用。
因此,如果两个因素联合在一起对因变量有显著的影响,则称这样的方差分析为有交互作用的方差分析。
4 方差分析实践操作
目前有许多统计工具和软件都可以实现方差分析,以下介绍几重最基础的操作。
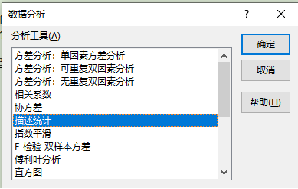
4.1 Excel
4.2 SPSS
4.3 R语言
可参阅:R语言——方差分析,其内容较为详细。
- 本文主要根据个人学习,并搜集部分网络上的优质资源总结而成,如有不足之处敬请谅解,欢迎批评指正、交流学习!
应用统计学与R语言实现学习笔记(八)——方差分析 ↩︎
数据分析技术MOOC ↩︎