数据结构&算法-----(8)单调栈和单调队列
数据结构&算法-----(8)单调栈和单调队列
- 单调栈
- 例题:Next Greater Number
- 算法复杂度分析
- LeetCode 第 739 题:气温列表
- Next Greater Number进阶,循环数组
- 单调队列
- 例题:滑动窗口的最值
- 1. 双端队列实现单调队列
- 算法复杂度分析
- 2. 数组实现单调队列
- 度小满2020实习生笔试题:滑动窗口池化操作
单调栈
栈(stack)是很简单的⼀种数据结构,先进后出的逻辑顺序,符合某些问题的特点,⽐如说函数调⽤栈。
单调栈实际上就是栈,只是利⽤了⼀些巧妙的逻辑,使得每次新元素⼊栈后,栈内的元素都保持有序(单调递增或单调递减)。
例题:Next Greater Number
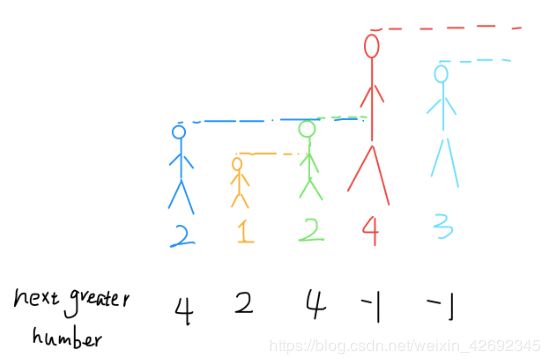
给你⼀个数组,返回⼀个等⻓的数组,对应索引存储着下⼀个更⼤元素,如果没有更⼤的元素,就存 -1。
输入:
[2,1,2,4,3]
输出
[4,2,4,-1,-1]
解释:
第⼀个 2 后⾯⽐ 2 ⼤的数是 4;
1 后⾯⽐ 1 ⼤的数是 2;
第⼆个 2 后⾯⽐ 2 ⼤的数是 4;
4 后⾯没有⽐ 4 ⼤的数,填 -1;
3 后⾯没有⽐ 3 ⼤的数,填 -1。
暴力法:
对每个元素后⾯都进⾏扫描,找到第⼀个更⼤的元素就⾏了。但是暴⼒解法的时间复杂度是 O(n^2)。
这个问题可以这样抽象思考:把数组的元素想象成并列站⽴的⼈,元素⼤⼩想象成⼈的⾝⾼。这些⼈⾯对你站成⼀列,如何求元素「2」的 Next Greater Number 呢?很简单,如果能够看到元素「2」,那么他后⾯可⻅的第⼀个⼈就是「2」的 Next Greater Number,因为⽐「2」⼩的元素⾝⾼不够,都被「2」挡住了,第⼀个露出来的就是答案。
单调栈结题模板 :
private static int[] nextGreaterElement(int[] nums) {
int length = nums.length;
int[] ans = new int[length];
Stack<Integer> stack = new Stack<>();
for (int i=length-1; i>=0; i--) {
while(!stack.isEmpty() && stack.peek()<=nums[i]) {
stack.pop(); //个子矮的退栈
}
ans[i] = stack.isEmpty() ? -1 : stack.peek(); //这个元素身后第一个高个子
stack.push(nums[i]);
}
return ans;
}
for 循环要从后往前扫描元素,因为我们借助的是栈的结构,倒着⼊栈,其实是正着出栈。
while 循环是把两个“⾼个”元素之间的元素排除,因为他们的存在没有意义,前⾯挡着个“更⾼”的元素,所以他们不可能被作为后续进来的元素的 Next Great Number 了。
算法复杂度分析
这个算法的时间复杂度不是那么直观,如果看到 for 循环嵌套 while 循环,可能认为这个算法的复杂度也是 O(n^2),但是实际上这个算法的复杂度只有 O(n)。
分析它的时间复杂度,要从整体来看:总共有 n 个元素,每个元素都被 push ⼊栈了⼀次,⽽最多会被 pop ⼀次,没有任何冗余操作。所以总的计算规模是和元素规模 n 成正⽐的,也就是 O(n) 的复杂度。
LeetCode 第 739 题:气温列表
根据每日气温列表,请重新生成一个列表,对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高,请在该位置用 0 来代替。
输入:
[73, 74, 75, 71, 69, 72, 76, 73]
输出:
[1, 1, 4, 2, 1, 1, 0, 0]
解释:
第⼀天 73 华⽒度,第⼆天 74 华⽒度,⽐ 73 ⼤,所以对于第⼀天,只要等⼀天就能等到⼀个更暖和的⽓温。
后⾯的同理。
//LeetCode739 气温列表
private static int[] dailyTemperatures(int[] T) {
int length = T.length;
int[] ans = new int[length];
Stack<Integer> stack = new Stack<>();
for (int i=length-1; i>=0; i--) {
while(!stack.isEmpty() && T[stack.peek()]<=T[i]) {
stack.pop();
}
ans[i] = stack.isEmpty() ? 0 : (stack.peek()-i); // 得到索引间距
stack.push(i); //加入索引,而不是元素
}
return ans;
}
另外一种思想,正向遍历,遇到后面一个大的数依次出栈并记录答案:
public int[] dailyTemperatures2(int[] T) {
int length = T.length;
int [] ans = new int[length];
Stack<Integer> stack = new Stack<Integer>();
//73, 74, 75, 71, 69, 72, 76, 73
for (int i=0; i<length; i++) {
while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
int index = stack.pop();
ans[index] = i-index;
}
stack.push(i);
}
return ans;
}
Next Greater Number进阶,循环数组
⾸先,计算机的内存都是线性的,没有真正意义上的环形数组,但是我们可以模拟出环形数组的效果,⼀般是通过 % 运算符求模(余数),获得环形特效:
int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
System.out.print(arr[index % n] + ", ");
index++;
}
回到 Next Greater Number 的问题,增加了环形属性后,问题的难点在于:这个 Next 的意义不仅仅是当前元素的右边了,有可能出现在当前元素的左边(如上例)。
明确问题,问题就已经解决了⼀半了。我们可以考虑这样的思路:将原始数组“翻倍”,就是在后⾯再接⼀个原始数组,这样的话,按照之前“比⾝⾼”的流程,每个元素不仅可以比较⾃⼰右边的元素,⽽且也可以和左边的元素比较了。
怎么实现呢?你当然可以把这个双倍⻓度的数组构造出来,然后套⽤算法模板。但是,我们可以不⽤构造新数组,⽽是利⽤循环数组的技巧来模拟。直接看代码吧:
private static int[] nextGreaterElement(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
Stack<Integer> stack = new Stack<>();
// 假装这个数组长度翻倍了
for (int i=2*n-1; i>=0; i--) {
while(!stack.isEmpty() && stack.peek()<=nums[i%n]) {
stack.pop(); //个子矮的退栈
}
ans[i%n] = stack.isEmpty() ? -1 : stack.peek(); //这个元素身后第一个高个子
stack.push(nums[i%n]);
}
return ans;
}
⾄此,你已经掌握了单调栈的设计⽅法及代码模板,学会了解决 Next Greater Number,并能够处理循环数组了。
单调队列
定义:队列中元素之间的关系具有单调性,而且,队首和队尾都可以进行出队操作,只有队尾可以进行入队操作。
为什么要学习单调队列:
- 对于维护好的单调队列,队内元素是有序的,那么取出最大值(最小值)的复杂度是O(1)
- 可以用来优化DP
如何维护单调队列:
- 队尾入队的时候维护其单调性
单调队列有两个性质:
- 队列中的元素其对应在原来的列表中的顺序必须是单调递增的
- 队列中元素的大小必须是单调递*(增/减/甚至是自定义也可以)
单调队列与普通队列不一样的地方就在于单调队列既可以从队首出队,也可以从队尾出队。
例题:滑动窗口的最值
洛谷:滑动窗口
原题传送门
同LeetCode第239题:
滑动窗口最大值
给定一个大小已知的数组,以及一个大小已知的滑动窗口,窗口每个时刻向后移动一位,求出每个时刻窗口中数字的最大值和最小值。(n<=1e6)
例如:
input:
8 3 长度为8的数组,滑动窗口大小为3
1 3 -1 -3 5 3 6 7
output:
每个时刻窗口中的最小值: -1 -3 -3 -3 3 3
每个时刻窗口中的最大值: 3 3 5 5 6 7
以求最小值为例分析:
- 维护一个单调递增的队列,每次滑动窗口入队之后取得一个区间最小值,取队列首元素即可
- 每次滑动窗口取最小值时,判断队首元素是否过期,过期则出队,继续寻找最小值
下文中我们用q来表示单调队列,p来表示其所对应的在原列表里的序号。
1 3 -1 -3 5 3 6 7
- 由于此时队中没有一个元素,我们直接令
1进队。此时,q={1},p={1}。 - 现在
3面临着抉择。下面基于这样一个思想:假如把3放进去,如果后面2个数都比它大,那么3在其有生之年就有可能成为最小的。此时,q={1,3},p={1,2} - 下面出现了
-1。队尾元素3比-1大,那么意味着只要-1进队,那么3在其有生之年必定成为不了最小值,原因很明显:因为当下面3被框起来,那么-1也一定被框起来,所以3永远不能当最小值。所以,3从队尾出队。同理,1从队尾出队。最后-1进队,此时q={-1},p={3} - 出现
-3,同上面分析,-1>-3,-1从队尾出队,-3从队尾进队。q={-3},p={4}。 - 出现
5,因为5>-3,同第二条分析,5在有生之年还是有希望的,所以5进队。此时,q={-3,5},p={4,5} - 出现
3。3先与队尾的5比较,3<5,按照第3条的分析,5从队尾出队。3再与-3比较,同第二条分析,3进队。此时,q={-3,3},p={4,6} - 出现
6。6与3比较,因为3<6,所以3不必出队。由于3以前元素都<3,所以不必再比较,6进队。因为-3此时已经在滑动窗口之外,所以-3从队首出队。此时,q={3,6},p={6,7} - 出现
7。队尾元素6小于7,7进队。此时,q={3,6,7},p={6,7,8}。
那么,我们对单调队列的基本操作已经分析完毕。因为单调队列中元素大小单调递*(增/减/自定义比较),因此,队首元素必定是最值。按题意输出即可。
1. 双端队列实现单调队列
以求最大值为例
public static int[] maxSlidingWindowByDeque(int[] nums, int k) {
int numsLength = nums.length;
if (numsLength <= 1 || k == 1)
return nums;
int ansLength = numsLength - k + 1;
int [] ans = new int [ansLength];
MonotonicQueueMax window = new MonotonicQueueMax();
int index=0;
for (int i=0; i<numsLength; i++) {
if (i < k-1) { // 先填满窗口的前 k-1 个数
window.push(nums[i]);
} else { // 窗口向前滑动
window.push(nums[i]);
ans[index] = window.max();
index++;
window.pop(nums[i-k+1]);
}
}
return ans;
}
//维护一个单调递减的队列, 可求滑动窗口最大值
class MonotonicQueueMax {
private Deque<Integer> data = new LinkedList<>();
//在队尾添加元素n
public void push(Integer n) {
while(!data.isEmpty() && data.peekLast()<n) {
data.pollLast();
}
data.addLast(n);
}
//返回当前队列中的最大值
public Integer max() {
return data.peekFirst();
}
//在队头删除元素n
public void pop(Integer n) {
if(!data.isEmpty() && data.peekFirst() == n) {
data.pollFirst();
}
}
}
算法复杂度分析
读者可能疑惑,push 操作中含有 while 循环,时间复杂度不是 O(1) 呀,那么本算法的时间复杂度应该不是线性时间吧?
单独看 push 操作的复杂度确实不是 O(1),但是算法整体的复杂度依然是O(N) 线性时间。要这样想,nums 中的每个元素最多被 push_back 和 pop_back ⼀次,没有任何多余操作,所以整体的复杂度还是 O(N)。
空间复杂度就很简单了,就是窗⼝的⼤⼩ O(k)。
2. 数组实现单调队列
以求最小值为例:
public static int[] minSlidingWindowByArray(int[] nums, int k) {
int numsLength = nums.length;
if (numsLength <= 1 || k == 1)
return nums;
int ansLength = numsLength - k + 1;
int [] ans = new int [ansLength];
int index=0;
/**
* 回顾用数组 queue 模拟队列时, 初始化 front=0, tail=-1
* 1. 入队: queue[++tail] = x
* 2. 出队: ++front (队首元素)
* 3. 判空: front>tail, 队列为空
* 4. 获取队头元素: queue[front]
*
* 用数组 queue 模拟 单调队列时, 仍初始化 front=0, tail=-1
* 1. 队尾入队: queue[++tail] = x
* 2. 队首元素出队: front++;
* 3. 队尾元素出队: tail--;
* 4. 获取队首元素: queue[front]
* 5. 获取队尾元素: queue[tail]
* 6. 判空 front>tail, 队列为空
*/
//维护一个单调递增的队列, 队首元素是滑动窗口最小值 的下标
int [] queue = new int[100000];
int front=0, tail=-1;
for (int i=0; i<numsLength; i++) {
//队列不空 && 队首元素(的下标) 在滑动窗口之外
if (front<=tail && queue[front]<i-k+1) {
//队首元素出队
front++;
}
//队列不空 && 队尾元素>=新元素
while(front<=tail && nums[queue[tail]]>=nums[i]) {
//队尾元素出队
tail--;
}
//新元素入队
queue[++tail] = i;
//初始滑动窗口填满之后, 便开始记录滑动窗口的最小值, 存在队首元素中
if (i+1>=k) {
ans[index] = nums[queue[front]];
index++;
}
}
return ans;
}
利用数组实现单调队列,其效率更高
度小满2020实习生笔试题:滑动窗口池化操作
解这个题的时候用了4个for的暴力法,太蠢了。
接下来讲一下怎么用单调队列来解:
先找出每行每个长度为b小区间的最大值,填在小区间的最右侧
再用上面的数据
纵向找出每个长度为a的小区间的(横向小区间最大值的)的最大值,即为滑动窗口的最大值,累加到答案中
另一种解释:
设max(i,j)存储的是(i,j−b+1)(i,j−b+2)...(i,j)的最大值
每一个格子的max(i,j)都求出来,这里使用单调队列,时间复杂度O(n^2)
再对上面的max矩阵进行纵向扫描
计算result(i,j)=max(max(i−a+1,j),max(i−a+2,j)...max(i,j))
即为每一个滑动窗口左上角(i−a+1,j−b+1),右下角(i,j)的最大值,累加起来即为答案
也是使用单调队列求出
时间复杂度O(n^2)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int a=sc.nextInt();
int b=sc.nextInt();
System.out.println("原池化矩阵为:");
for (int i=1; i<=n; i++) {
for (int j=1; j<=m; j++) {
System.out.print((i*j)%10 + ", ");
}
System.out.println();
}
long ans=0;
//hang记录横向扫描结果
int hang[][]=new int[n+1][m+1];
int que[]=new int[1000+10];
int front=0;
int tail=0;
/**
* 注意与初始化front=0, tail=-1时方式的区别
*
* 用数组 queue 模拟 单调队列时, 仍初始化 front=0, tail=0
* 1. 队尾入队: queue[tail++] = x
* 2. 队首元素出队: front++;
* 3. 队尾元素出队: tail--;
* 4. 获取队首元素: queue[front]
* 5. 获取队尾元素: queue[tail-1]
* 6. 判空 front>=tail, 队列为空
*/
for(int i=1; i<=n; i++) {
front=0;
tail=0;
//横向扫描, 窗口大小是b
for(int j=1; j<=m; j++) {
//队列不空 && 队首元素(的下标) 在滑动窗口之外
while(front<tail && (que[front]<j-b+1))
//队首元素出队
front++;
//队列不空 && 队尾元素<=新元素
while(front<tail && (i*que[tail-1])%10<=(i*j)%10)
//队尾元素出队
tail--;
//新元素入队
que[tail++]=j;
//记录横向扫描结果
hang[i][j]=(i*que[front])%10;
}
}
System.out.println("横向扫描结果为:");
for(int i=0; i<=n; i++) {
for (int j=0; j<=m; j++) {
System.out.print(hang[i][j]+", ");
}
System.out.println();
}
//n行m列, a行b列
//hang[][] 是 (n+1)*(m+1) 的矩阵, 故列数 i 有 b<=i<=m
for(int i=b; i<=m; i++) {
front=0;
tail=0;
//纵向扫描, 窗口大小是a
for(int j=1; j<=n; j++) {
//队列不空 && 队首元素(的下标) 在滑动窗口之外
while(front<tail && (que[front]<j-a+1))
//队首元素出队
front++;
//队列不空 && 队尾元素<=新元素
//注意: j是行标, i是列标
while(front<tail && hang[que[tail-1]][i]<=hang[j][i])
//队尾元素出队
tail--;
//新元素入队, 注意存的是行标
que[tail++]=j;
//纵向扫描后, 记录结果
if(j>=a){
System.out.println(j+", "+i+", "+hang[que[front]][i]);
ans+=1L*hang[que[front]][i];
}
}
}
System.out.println(ans);
}
}