基于逻辑回归算法的大学招生录取预测项目

1. 介绍

逻辑回归是一种广义的线性回归分析模型，通常用于数据挖掘，疾病自动诊断，经济预测等领域。本报告应用python语言中的scikit-learn模块下的逻辑回归模型(LogisticRegression), 对数据集LogiReg_data.csv中记录的100组考试分数和大学录取情况进行机器学习和预测。本算法是一种二分类算法。

数据集来源：https://blog.csdn.net/u010331646/article/details/95453212

2. 查看数据基本情况

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
import warnings

#忽略掉不影响正常运行的警告提示
warnings.filterwarnings("ignore") 
path = r"D:\python\course\Kaikeba\project\dataSet\LogiReg_data.csv"
data = pd.read_csv(path)
print(data.head())
print(data.shape)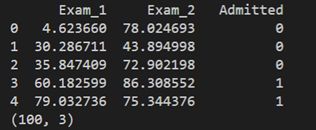

可以看到这个数据集由100行，3列数据组成。特征名称为科目1，科目2，录取（Admitted）。录取栏中的1代表被录取，0代表未录取。我们查看一下录取的情况，也就是录取和未录取的总人数。

print(data.groupby("Admitted")["Admitted"].count()) 

可以看到有60人被成功录取，而40人未被录取。

3. 模型训练与预测
使用sklearn中的train_test_split函数将数据集划分成训练集和测试集。然后使用LogisticRegression()函数定义一个对象，并传入训练集数据对该对象进行训练。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split 

X = data.iloc[:, :2]
y = data.iloc[:, 2:] 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=2)
lr = LogisticRegression()
lr.fit(X_train, y_train)
y_hat = lr.predict(X_test)
print("权重：", lr.coef_)
print("偏置：", lr.intercept_)
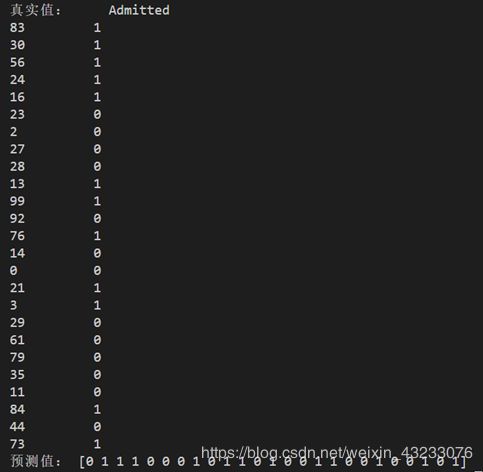
print("真实值：", y_test)
print("预测值：", y_hat)

4. 绘制数据集的散点图

c1 = data[data["Admitted"]==0]
c2 = data[data["Admitted"]==1] 
plt.scatter(x=c1.values[:, 0], y=c1.values[:, 1], c="#2b4750", label="Not Admitted")
plt.scatter(x=c2.values[:, 0], y=c2.values[:, 1], c="#dc2624",
marker='p', label="Admitted")
plt.xlabel("Exam 1")
plt.ylabel("Exam 2")
plt.title("Admission Distribution") 
plt.legend(loc="lower left") 
plt.show()

可以看到两组数据之间基本有一个清晰的界限。

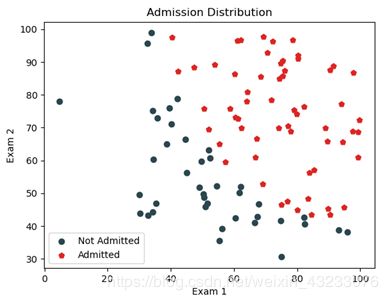
5. 对预测结果可视化

import matplotlib
as mpl  

plt.figure(figsize=(10, 4))
# 为了在绘图中可以显示中文，需要设置rcParams参数
mpl.rcParams['font.sans-serif'] = ['SimHei'] 
y_hat = pd.DataFrame(data=y_hat, index=y_test.index) 
plt.plot(y_test, marker="o", ls="", ms=15, c="r", label="真实类别")
plt.plot(y_hat, marker="X", ls="", ms=15, c="g", label="预测类别")
plt.legend()
plt.xlabel("样本序号", fontsize=16)
plt.ylabel("类别",fontsize=16)
plt.title("逻辑回归分类预测结果", fontsize=20) 
plt.show()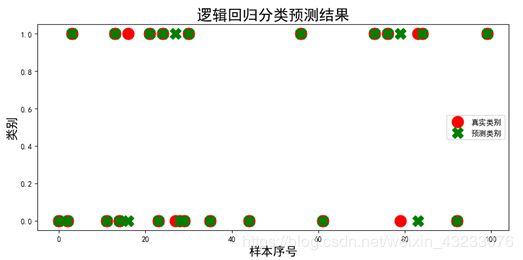 

可以看到绝大部分数据的真实类别和预测类别还是吻合的非常好的。

6. 绘制决策边界

我们定义一个绘制决策边界的函数。

from matplotlib.colors import ListedColormap 

# 定义函数，用于绘制决策边界。
def plot_decision_boundary(model, X, y):
    color = ["#2b4750", "#dc2624", "b"]
    marker = ["o", "p", "x"] 
    class_label = np.unique(y)
    cmap = ListedColormap(color[: len(class_label)])
    x1_min, x2_min = np.min(X, axis=0)
    x1_max, x2_max = np.max(X, axis=0)
    x1 = np.arange(x1_min - 1, x1_max + 1, 0.02)
    x2 = np.arange(x2_min - 1, x2_max + 1, 0.02)
    X1, X2 = np.meshgrid(x1, x2)
    Z = model.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape)

    # 绘制使用颜色填充的等高线。
    plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5)
    for i, class_ in enumerate(class_label):
        plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1], =cmap.colors[i], label=class_, marker=marker[i])
    plt.legend()
    plt.show()

# 用训练集绘制左图
X_train = np.array(X_train)
y_train = np.array(y_train).flatten()
plot_decision_boundary(lr, X_train, y_train)

# 用测试集绘制右图
X_test = np.array(X_test)
y_test = np.array(y_test).flatten()  
plot_decision_boundary(lr, X_test, y_test)

我们调用该函数，分别绘制模型在训练集和测试集上的划分效果。

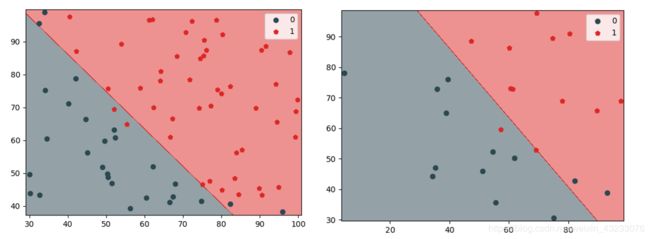
7. 绘制录取概率曲线

from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression 

linear_model = LinearRegression()
linear_model.fit(data[["Exam_1"]], data["Admitted"])
logistic_model = LogisticRegression()
logistic_model.fit(data[["Exam_1"]], data['Admitted']) 
logistic_model = LogisticRegression()
logistic_model.fit(data[["Exam_1"]], data["Admitted"])

# 这里的 predict_proba 函数实际为一个概率值
pred_probs = logistic_model.predict_proba(data[["Exam_1"]])

# pred_probs[:, 1] 这里的参数 1 表示被录取的可能性，0 为没被录取的可能性
plt.scatter(data["Exam_1"], pred_probs[:, 1], c='g')
plt.xlabel("Exam 1 Score")
plt.ylabel("Probability of Admittance")
plt.title("Admission Probability on Exam 1 Score")  
plt.legend(loc="lower left")
plt.show()

predict_proba()返回的是一个 n 行 k 列的数组， 第 i 行 第 j 列上的数值是模型预测 第 i 个预测样本为某个标签的概率，并且每一行的概率和为1。从下面两张图可以看到：大约在60分的时候，Exam1和Exam2都有大约50%的录取率。

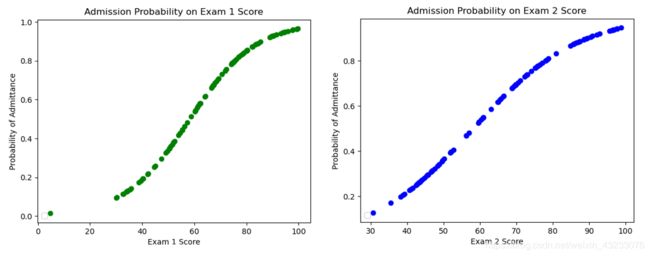
# 我们也可以通过 predict 函数直接预测值, 即要不是1或者0
logistic_model = LogisticRegression()
logistic_model.fit(data[["Exam_1"]], data["Admitted"])
fitted_labels = logistic_model.predict(data[["Exam_1"]])
plt.scatter(data["Exam_1"], fitted_labels, c='r')
plt.xlabel("Exam 1 Score")
plt.ylabel("Admittance/No admittance")
plt.title("Admission Distribution on Exam 1 Score") 
plt.show()

下图是直接使用logistic_model.predict()函数进行预测的结果。可以看到决策边界大约在60分。

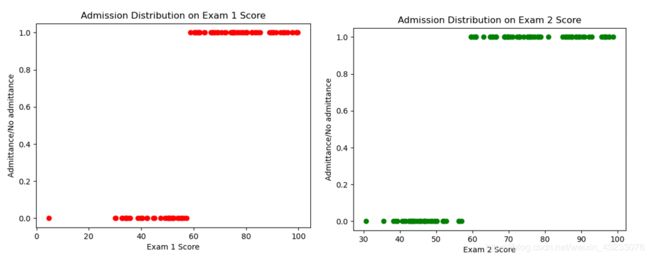
8. 计算预测的精确度(precision)

假设TP，FP，TN，FN四个缩写符号，分别表示如下含义。

• TP：真正例，实际上是正例的数据点被标记为正例。
• FP：假正例，实际上是反例的数据点被标记为正例。
• TN：真反例，实际上是反例的数据点被标记为反例。
• FN：假反例，实际上是正例的数据点被标记为反例。

那么精确度(precision)定义为：

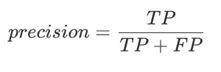
我们用如下代码计算精确度。

labels = logistic_model.predict(data[["Exam_1"]]) 
data["predicted_label"] = labels 
data["actual_label"] = data["Admitted"]
matches = data["predicted_label"] == data["actual_label"] 
correct_predictions = data[matches]
accuracy = len(correct_predictions) / float(len(data)) 
print(accuracy) 

下面的代码计算了真正被录取的和真正未被录取的数量。

true_positive_filter = (data["predicted_label"] == 1) & (data["actual_label"] == 1) 
true_positives = len(data[true_positive_filter])
true_negative_filter = (data["predicted_label"] == 0) & (data["actual_label"] == 0)
true_negatives = len(data[true_negative_filter])
print(true_positives)
print(true_negatives)

9.计算召回率(Recall rate)和特异性(specificity)

召回率用如下公式定义：

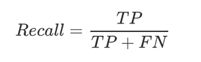
召回率代表了预测出的成功录取数和总的实际录取数的比率。这个指标反映了模型在多大程度上能把所有的目标找出来。我们用如下代码计算该数据集的召回率。

# 检测召回率
true_positive_filter = (data["predicted_label"] == 1) & (data["actual_label"] == 1)
true_positives = len(data[true_positive_filter])
false_negative_filter = (data["predicted_label"] == 0) & (data["actual_label"] == 1)
false_negatives = len(data[false_negative_filter])
sensitivity = true_positives / float((true_positives + false_negatives))
print(sensitivity)

特异性用如下公式定义：

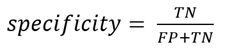
特异性代表了实际未录取总人数中经模型识别为未录取的样本数所占的百分比。这个指标反映了模型不误判的概率。我们用如下代码计算该数据集的特异性。

# 检测特异性
true_negative_filter = (data["predicted_label"] == 0) & (data["actual_label"] == 0)
true_negatives = len(data[true_negative_filter])
false_positive_filter = (data["predicted_label"] == 1) & (data["actual_label"] == 0)
false_positives = len(data[false_positive_filter])
specificity = true_negatives / float((false_positives + true_negatives))
print(specificity)

10. 绘制ROC曲线

ROC曲线（Receiver Operating Characteristic Curve）能反映该模型在选取不同阈值的时候其召回率和其特异性的趋势走向。我们用如下代码绘制该数据集的ROC曲线。

from sklearn import metrics

shuffled_index = np.random.permutation(data.index)
shuffled_data = data.loc[shuffled_index]
train = shuffled_data.iloc[0:70]
test = shuffled_data.iloc[70:len(shuffled_data)] 

# 通过测试集进行
model = LogisticRegression()
model.fit(train[["Exam_1"]], train["actual_label"])
labels = model.predict(test[["Exam_1"]])
test["predicted_label"] = labels
probabilities = model.predict_proba(test[["Exam_1"]])
fpr, tpr, thresholds = metrics.roc_curve(test["actual_label"], probabilities[:, 1])
print(thresholds)
plt.plot(fpr, tpr, c='r') 
plt.show()

本模型绘制的ROC曲线：

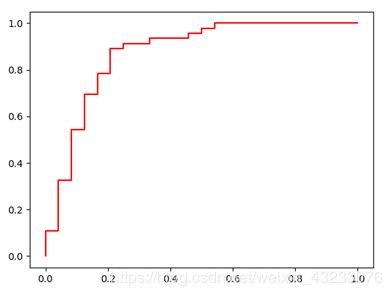
下面的代码可以计算上图红色曲线下方的面积，也就是AUC(area under curve)值。

from sklearn.metrics import roc_auc_score 

auc_score = roc_auc_score(test["actual_label"], probabilities[:, 1])
print(auc_score)

11. 用scikit-learn做S折交叉验证

S折交叉验证会把样本数据随机的分成S份，每次随机的选择S-1份作为训练集，剩下的1份做测试集。当这一轮完成后，重新随机选择S-1份来训练数据。这里，我们使用scikit-learn模块中的KFold和cross_val_score来进行交叉验证。这里S取5。

import pandas as pd
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score  

path = r"D:\python\course\Kaikeba\project\dataSet\LogiReg_data.csv"
data = pd.read_csv(path)
data["actual_label"] = data["Admitted"]
data = data.drop("Admitted", axis=1)
kf = KFold(5, shuffle=True, random_state=42) 
lr = LogisticRegression() 

# ROC
accuracies = cross_val_score(lr, data[["Exam_1"]], data["actual_label"], scoring="roc_auc", cv=kf)
average_accuracy = sum(accuracies) / len(accuracies)  

print(accuracies)
print(average_accuracy)