机器学习——回归(OLS、LWLR、岭回归、前向逐步回归、lasso、缩减系数方法)
ps:《机器学习实战》学习记录
知识点:最小二乘、局部加权线性回归、系数缩减、岭回归、lasso、前向逐步回归
背景
“回归”的目的是预测数值型的目标值。例如,给定一个数据集,其中包含多种汽车价钱P和销量W的对应关系,通过回归算法可以预测出W-P的函数解析式,从而可以预测新生产汽车的定价P对应未来一段时间的销量。
因此,回归算法的核心在于确定一个解析式。
相关回归算法
1. 普通最小二乘法(OLS, ordinary least squares)
1.1. 思想:
对于给定的数据集上,求出最佳拟合直线,保证数据集的所有点到直线的距离之和最近。
- 已知点到预测直线的距离,可以理解成预测拟合直线的误差。这里使用平方误差来刻画:
∑ i = 1 n ( y i − x i T ω ) 2 \displaystyle\sum_{i=1}^{n}(y_i-x_i^T\omega)^2 i=1∑n(yi−xiTω)2
即确定一个 ω \omega ω,使上式值最小。 - 在计算机中,使用向量工具处理更为简便,最小二乘思想可通过下面的式子计算出 ω \omega ω值:
ω = ( X T X ) − 1 X T y \omega=(X^TX)^{-1}X^Ty ω=(XTX)−1XTy
1.2. 程序实现(基于python):
#将给定的数据集格式化处理,使向量化
def loadDataSet(filename):
numFeat = len(open(filename).readline().split('\t')) - 1
dataMat = []; labelMat = []
fr =open(filename)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append([float(curLine[-1])])
return dataMat,labelMat
#最小二乘法的实现
def standRegres(xArr, yArr):
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T * xMat
if linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * yMat)
return ws
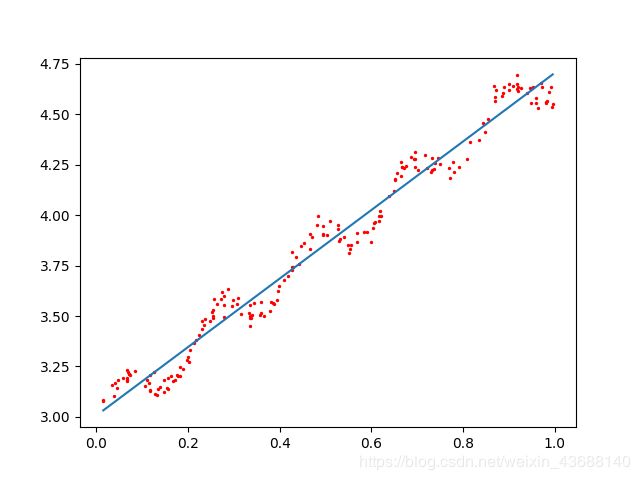
显然,这种用直线拟合的方法普适性不强,如下图所示,线性回归存在欠拟合的现象,预测效果可能不佳。

2.局部加权线性回归(LWLR, Locally Weighted Linear Regression)
2.1 思想
给待测点附近的每一个点都赋予一定权重,距离越近赋予的权重越大。LWLR算法中可使用高斯核赋予对应权重:
ω ( i , i ) = e x p ( ∣ x ( i ) − x ∣ − 2 k 2 ) \omega(i,i)=exp(\frac{|x^{(i)}-x|}{-2k^2}) ω(i,i)=exp(−2k2∣x(i)−x∣)
公式中 ω ( i , i ) \omega(i,i) ω(i,i)为第i个样本点的权重,可以看出离预测点越近的点,对应权重 ω \omega ω越大;此外,参数k是由我们自行确定的,k越小,距离待测点附近的样本点权重越大,离待测点较远处样本点权重较小。
可以理解为,k越小,则用于训练回归的样本点越少,因为权重大的样本点对结果影响更大。(有话语权的点更少)
其中,使用LWLR方法的回归系数计算公式为:
ω = ( X T W X ) − 1 X T W y \omega=(X^TWX)^{-1}X^TWy ω=(XTWX)−1XTWy
2.2 python程序
def lwlr(testPoint, xArr, yArr, k=1.0):
xmat = mat(xArr); ymat = mat(yArr).T
m=shape(xmat)[0] #m为样本数
weights=mat(eye((m))) #创建对角矩阵
for i in range(m):
diffMat = testPoint-xmat[i,:]
weights[i,i]=exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xmat.T * (weights * xmat)
if linalg.det(xTx) == 0 :
print("this matrix is singular, cannot do inverse")
return
ws = xTx.I * (xmat.T *(weights * ymat))
return testPoint * ws
def lwlrTest(testArr, xarr, yarr, k=1.0):
m = shape(testArr)[0]
yhat = zeros(m)
for i in range(m):
yhat[i] = lwlr(testArr[i], xarr, yarr, k)
return yhat
2.3不同k值的结果对比
规律:k越小,曲线在给定的样本集上拟合得更好。
注意事项:
- 一般而言,在给定数据集上拟合过好,则对未知数据的预测效果更差,称为“过拟合”现象。k过小时,将给定数据集中的噪声点纳入太多,反而不能体现数据的客观规律,即拟合出的曲线泛化能力不足。
- 局部加权线性回归计算量大,对每个点预测的时候,都需要使用整个数据集。实际上从高斯核函数可以看出,离待预测点较远处的数据点权重很小,对于后续样本的刻画几乎不起任何作用。
3. 缩减系数
3.1 背景
经常会遇到一种情况:数据集的特征数比样本数多,即对于m×n的数据集矩阵 X X X,m
3.2 岭回归
3.2.1 原理
在矩阵 X T X X^TX XTX上加入一个 λ I \lambda I λI,从而使矩阵可逆,矩阵 I I I为m×m的单位矩阵,其权重计算公式为:
ω = ( X T X + λ I ) − 1 X T y \omega=(X^TX+\lambda I)^{-1}X^Ty ω=(XTX+λI)−1XTy
此处通过引入 λ \lambda λ来限制所有 ω \omega ω之和,此惩罚项可以减少不重要参数,统计学中称为缩减shrinkage。
岭回归除了可以处理n>m的情况时,现在还用于在估计中加入偏差,从而得到更好的估计
岭回归中的“岭”,体现在单位矩阵I上,对角线元素全为1,形状像一个山岭
3.2.2 python实现
def ridgeRegres(xmat, ymat, lam = 0.2):
xTx = xmat.T * xmat
denom = xTx + eye(shape(xmat)[1]) * lam
if linalg.det(denom) == 0.0:
print("this matrix can not inverse!")
return
ws = denom.I * (xmat.T *ymat)
return ws
def ridgeTest(xarr, yarr):
xmat = mat(xarr); ymat = mat(yarr)
ymean = mean(ymat,0)
ymat = ymat - ymean
xmeans = mean(xmat, 0)
xvar = var(xmat,0)
xmat = (xmat-xmeans)/xvar
numTestPts = 30
wmat = zeros((numTestPts, shape(xmat)[1]))
for i in range(numTestPts): #此处训练出30个不同的ws,对应不同的lambda值
ws = ridgeRegres(xmat, ymat, exp(i-10)) #lambda值以指数级变化,从而可以看出极大和极小值对结果的影响
wmat[i,:]=ws.T
return wmat
收获:
- lambda值以指数级变化,从而可以看出极大和极小值对结果的影响(lambda为python保留字)
- 样本数据标准化处理:平衡所有大小数据的权重
- var(), linalg.det(), mean()
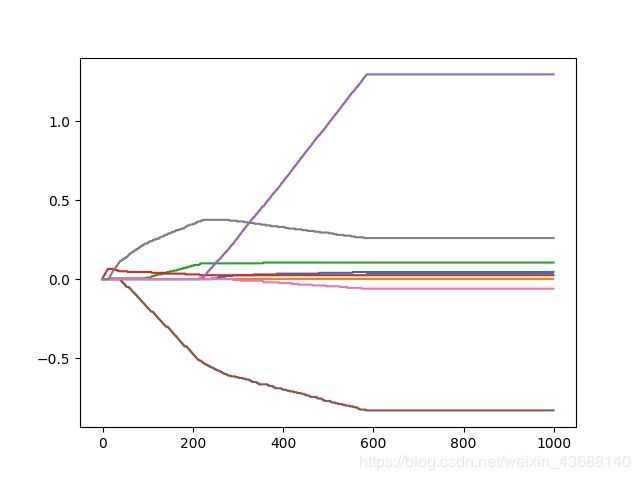
3.2.3 结果

可见, λ \lambda λ很小的时候,系数与普通回归类似; λ \lambda λ较大时,所有系数缩减为0( λ \lambda λ大,对系数的“惩罚”力度大)
3.3 lasso
首先,在普通最小二乘法上增加限制条件:
∑ k = 1 n ω k 2 ≤ λ \displaystyle\sum_{k=1}^{n}\omega_k^2\le\lambda k=1∑nωk2≤λ
即可得到岭回归一样的公式
lasso缩减方法是增加限制条件:
∑ k = 1 n ∣ ω k ∣ ≤ λ \displaystyle\sum_{k=1}^{n}|\omega_k|\le\lambda k=1∑n∣ωk∣≤λ
这里用绝对值代替平方和,来约束 ω \omega ω,当 λ \lambda λ足够小时,某些系数会被迫缩减为0,这样可以帮助我们理解数据。
3.4 前向逐步回归
3.4.1 原理
这是一种贪心算法,每一步都尽可能地减小误差。首先初始化所有权重为1,然后每一步做出决策:对权重增加或减少一个很小的值,通过比较改变权重后误差的变化来进行决策。
3.4.2 python实现
def stageWise(xArr,yArr,eps=0.01,numIt=100):
xMat = mat(xArr); yMat=mat(yArr).T
yMean = mean(yMat,0)
yMat = yMat - yMean #can also regularize ys but will get smaller coef
xMean = mean(xMat, 0)
xvar = var(xMat, 0)
xMat = (xMat-xMean)/xvar
m,n=shape(xMat)
returnMat = zeros((numIt,n)) #testing code remove
ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
for i in range(numIt):
print (ws.T)
lowestError = inf;
for j in range(n):
for sign in [-1,1]:
wsTest = ws.copy()
wsTest[j] += eps*sign
yTest = xMat*wsTest
rssE = rssError(yMat.A,yTest.A)
if rssE < lowestError:
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i,:]=ws.T
return returnMat
- python中使用inf表示无穷大